XDRender_ShaderMode_StandardLit(1) 物理渲染-默认PBR-实现(1)
XDRender_ShaderMode_StandardLit(1) 物理渲染-默认PBR-实现(1)
@白袍小道


前言
理论部分可以参考PRT部分、RealTimeRender,网上大部分资料.
其中相互联系图-参考
https://www.cnblogs.com/BaiPao-XD/p/13751667.html
这里特别推荐
毛星云:
https://zhuanlan.zhihu.com/p/56967462
以及博主关于法线分布函数和几何分布的总结.
文刀秋二:
https://zhuanlan.zhihu.com/p/20091064
正文
这里作为实现部分,主要是考虑三件事:
1、HLSL的结构,BRDF的相关数据结构,以及传递和组织这些数据
2、关于菲涅尔反射、法线分布函数、几何分布函数、积分处理部分
3、公式的演化、特性、以及实现和组织部分
先放出一个数据流图
一、理论引进
简化公式
第一个大公式类
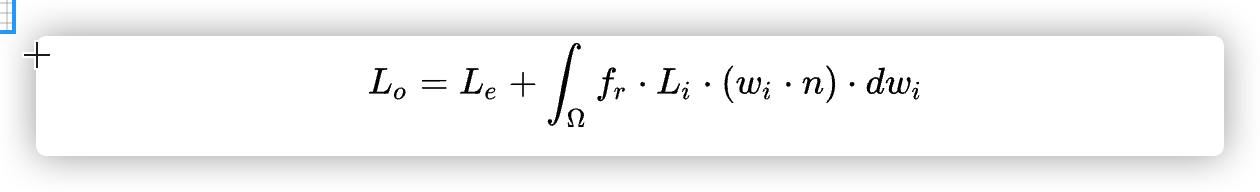
参数说明:

第二个大公式类
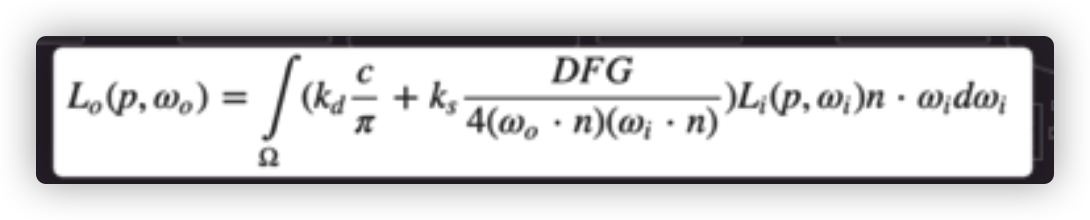
拆开后
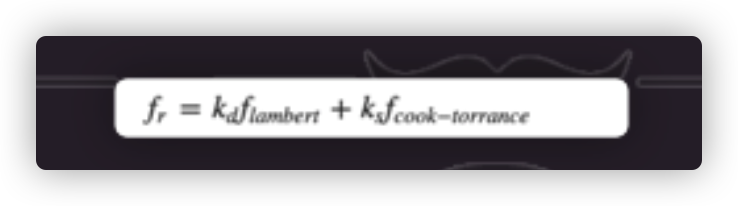
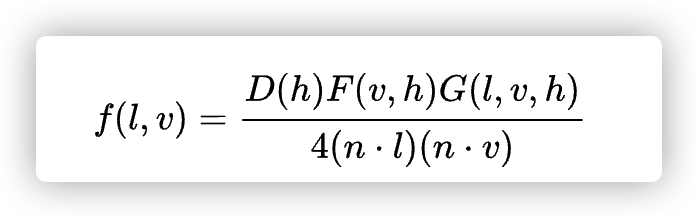
对于每一个细节部分实现中会单独说明和处理, 抱着敬畏和大胆的步伐,开始实现.
光和介质的交互
当一束光线入射到物体表面时,由于物体表面与空气两种介质之间折射率的快速变化,光线会发生反射和折射:
- 反射(Reflection)。光线在两种介质交界处的直接反射即镜面反射(Specular)。金属的镜面反射颜色为三通道的彩色,而非金属的镜面反射颜色为单通道的单色。
- 折射(Refraction)。从表面折射入介质的光,会发生吸收(absorption)和散射(scattering),而介质的整体外观由其散射和吸收特性的组合决定,其中:
- 散射(Scattering)。折射率的快速变化引起散射,光的方向会改变(分裂成多个方向),但是光的总量或光谱分布不会改变。散射最终被视作的类型与观察尺度有关:
- 次表面散射(Subsurface Scattering)。观察像素小于散射距离,散射被视作次表面散射。
- 漫反射(Diffuse)。观察像素大于散射距离,散射被视作漫反射。
- 透射(Transmission)。入射光经过折射穿过物体后的出射现象。透射为次表面散射的特例。
- 吸收(Absorption)。具有复折射率的物质区域会引起吸收,具体原理是光波频率与该材质原子中的电子振动的频率相匹配。复折射率(complex number)的虚部(imaginary part)确定了光在传播时是否被吸收(转换成其他形式的能量)。发生吸收的介质的光量会随传播的距离而减小(如果吸收优先发生于某些波长,则可能也会改变光的颜色),而光的方向不会因为吸收而改变。任何颜色色调通常都是由吸收的波长相关性引起的。
二、实现过程
假定最最最理想的情况
这里实现我们先假设一大堆条件,避免分散注意.比如多直接光,环境光照, 光衰减, 透射,暂时不守恒,只包含Forward方式等等大量的条件.
我们的最简化参数: 粗超度, 基础颜色, 金属度
流程
入口:这里是Shader部分, 通过填写LightMode启用,(LightMode被OpoPass识别)
其实我们也可以将直接光的数据在前面的阶段(比如ConfigLightPass, Deff的话是先搞出光照需要所有纹理数据,再等到后续直接进行对纹理处理)传递.当然这是
第一步: XDRender/ShaderMode/DefaultLit.Shader
第二步: 进入到构建必要数据
a、Surface:这里是将Shader数据处理为统一, 比如一些用BaseColor纹理,一些不用.这样我们到这里统一搞出Color.
#ifdef _DIFFCUSE_MAP
half4 albedoAlpha = _BaseColor * SAMPLE_TEXTURE2D(_DiffcuseMap,sampler_DiffcuseMap, input.baseUV);
#else
half4 albedoAlpha = _BaseColor;
#endif
outSurfaceData.alpha = albedoAlpha.r;
outSurfaceData.albedo = albedoAlpha.rgb;
float3 rmao_sample = SAMPLE_TEXTURE2D(_RouAOMap,sampler_RouAOMap, input.baseUV).b * _OcclusionStrength;
outSurfaceData.metallic = rmao_sample.r;
outSurfaceData.specular = _SpecColor;
outSurfaceData.smoothness = 1.0-rmao_sample.g;
b、Input:顶点属性相关
nputData.viewDirectionWS = normalize(_WorldSpaceCameraPos.xyz - input.positionWS.xyz);
inputData.positionWS = input.positionWS;
inputData.normalWS = normalWS;
inputData.bakedGI = SAMPLE_GI(lightmapUV, input.vertexSH, inputData.normalWS);
第三步:组织BRDF的数据结构
第四步:
BRDF必要数据
1、这里我们就不考虑两种PBR数据流区别,先就简单把数据传过来
2、我们先简单传递,然后在下一步过程中去处理金属和电解质的特殊性.
注意一下,HLSL可以类似多态的函数写法,还可以建立多个InitializeBRDFData辅助与宏来处理多种数据结构. 减少不断增加.
这里还可以YY一下, 就一种Float4 * X结构去组织
inline void InitializeBRDFData(half3 albedo, half metallic, half3 specular, half smoothness, half alpha,
out BRDFData outBRDFData)
{
//http://richbabe.top/2018/06/25/%E6%8E%A2%E7%A9%B6PBR%E7%9A%84%E4%B8%A4%E7%A7%8D%E6%B5%81%E7%A8%8B%E4%BB%A5%E5%8F%8AUnity%E4%B8%AD%E7%9A%84PBS/
outBRDFData.diffuse = albedo;
outBRDFData.specular = specular;
outBRDFData.grazing = saturate(smoothness + 1 - metallic);
outBRDFData.perceptualRoughness = PerceptualSmoothnessToPerceptualRoughness(smoothness);
outBRDFData.roughness = max(PerceptualRoughnessToRoughness(outBRDFData.perceptualRoughness), HALF_MIN);
outBRDFData.roughness2 = outBRDFData.perceptualRoughness * outBRDFData.perceptualRoughness;
outBRDFData.lerpRoughness = lerp(0.01, 1.0, outBRDFData.perceptualRoughness);
outBRDFData.metallic = metallic;
outBRDFData.clearcoat = 0;
outBRDFData.clearcoatgloss = 0;
outBRDFData.secondcolor=0;
BRDF计算
这里我们只关注BSDF中的BRDF的直接光照部分,其中光照按照介质的不同对光照会做不同的分化影响
0 基础参数计算
主要是计算 :法向量(宏观非亚像素),入射点光照方向, 射点视野, 半角方向(这里注意一般来说主要使用的NH来作为后续几个函数的因变量, 推导过程网上已经大量这里就不详细说明)几个向量的叉积.
注意:这里我们就会注意到是在采样点进行的计算, 所以这几个参数不是物理意义上的点,偏差出现.但整体相对可接受.
float3 halfVector = normalize(lightDir + viewDir); //半角向量
float nl = max(saturate(dot(normal, lightDir)), 0.000001); //防止除0
float vh = max(saturate(dot(viewDir, halfVector)), 0.000001);
float lh = max(saturate(dot(lightDir, halfVector)), 0.000001);
float nh = max(saturate(dot(normal, halfVector)), 0.000001);
float nv = max(saturate(dot(normal, viewDir)), 0.000001);
为何是半角?
URL:
1 确定漫反射和镜面反射的比例
这里我们假定光线在介质交界处(默认为空气到其他),只发生了漫反射和镜面反射,两者合起来辐射度为入射处光线辐射度,从而满足一定意义上的能量守恒原则.
所以我们需要对这个比例进行计算,反过来说于分配辐射度.
L=Kd^Diff + Ks^Spec
其中这两个参数,主要会受到介质的影响.
a\金属度(或高光):
| 金属度 | 表示了反射时发生镜面反射和漫反射的光线的占比。 |
|---|---|
| Metallic度越大 | 发生镜面反射的占比越大,漫反射diffuse占比越小,一般金属物体的金属度比较大:70% ~ 100%之间; |
| Metallic越小 | 发生镜面反射的占比越小,漫反射diffuse占比越大,一般非金属物质金属度比较小;2% ~ 5%之间,宝石的大概8%; |
b\菲涅尔反射.
(这里注意是金属菲涅而F0是带有颜色,具体我们在后详细)
可参考代码如下:
loat3 F0 = float3(0.04,0.04,0.04);
//使用mix(lerp)函数利用 metallic对diffuse,最低值做插值,
//metallic越接近0,那么就越接近绝缘体,
//metalness越接近1,那么就越接近金属的Diff。
F0 = lerp(F0, pBRDF.diffuse, pBRDF.metallic);
float3 F = BaseFresnelSchlick(vh,F0);
float3 kS = F;
float3 kD = float3(1.0,1.0,1.0) - kS;
kD *= 1.0 - pBRDF.metallic;
这里我们也可以提前将Diff进行减弱.
先(1.0-0.04 ) - (pBRDF.metallic)(1.0-0.04 ),然后Diff = Diff *这个值来修复Diff
#define kDieletricSpec half4(0.04, 0.04, 0.04, 1.0-0.04)
half OneMinusReflectivityMetallic(half metallic)
{
half oneMinusDielectricSpec = kDieletricSpec.a;
return oneMinusDielectricSpec - metallic * oneMinusDielectricSpec;
}
有了这个比例我们可以先假定已经计算出漫反射和镜面高光反射
float3 DirectLightResult = (kD * pBRDF.diffuse + specular) * lightColor * nl;
return DirectLightResult;
///------------直接光照部分--------------------
vLight = GetMainLight ();
lightDir= normalize(vLight.direction).xyz;
lightColor= vLight.color * (1-vLight.distanceAttenuation);
DirectLightResult += BRDF01_DirectLight(lightColor,normal,lightDir,viewDir,pBRDFData);
2 菲涅尔反射
定义:根据物理学,麦克斯韦方程组可以在折射率(IOR)变化时计算光的行为。对于空气中通常的物体表面而言,物体的表面便是空气折射率和物体折射率的交界面,对此特殊的折射率交界面而言,麦克斯韦方程组的解被我们称为菲涅尔方程
a\万物皆有菲涅尔效应?
在宏观层面看到的实际上是微观层面微平面菲涅尔效应
(表示观察看到的反射光线的量与视角相关的现象,且掠射角度(90度)
下反射率最大)的平均值,即影响菲涅尔效应的关键参数在于每个微平面
的法向量和入射光线的角度,而不是宏观平面的法向量和入射光线的角度
b\其中F0的含义是
F0即0度角入射的菲涅尔反射率。任意角度的菲涅尔反射率
b1 简化的公式
可由F0和入射角度计算得出,而上文我们提到过不同的材质(物理意义上)
对算法有一定的区别,比如非金属的F0是一个float,金属的F0是一个float3. 这
样就暗示一个比较重要的问题如何去统一的处理.?总不能if/#if几个吧, 况且
对美术而言很难去规定这个含义并记录.

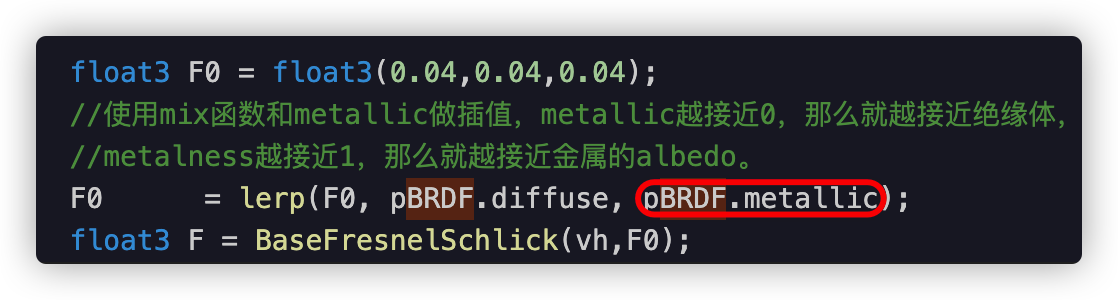
这里电介质具有相当低的F0值 - 通常为0.06或更低, 故而我们用这个边界值0.04来模拟一下
b2 通过IOR来处理
以上只是一种最简化的求F0, 而光在传播到两种不同介质交界处时,原始光波和新的光波的相速度(Phase Velocity)的比率定义了介质的光学性质,就是折射率(Index of Refraction,IOR)故而我们还有通过IOR来实现.
而这个折射率,我们可以通过查找表( 或者说将表编码:https://link.zhihu.com/?target=https%3A//github.com/QianMo/PBR-White-Paper/raw/master/bonus/%255BPBR-White-Paper%255D%2520PBR-Material-F0-Quick-Reference-Chart.pdf 转为纹理查找等等方式)
(这里补充F0为0度角入射时的菲涅尔反射率。而折射(refracted)到表面中的光量则为为1-F0。)
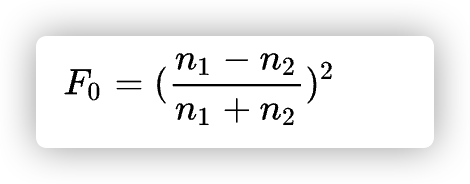
但我们大部分是空气到其他,故而可以换成
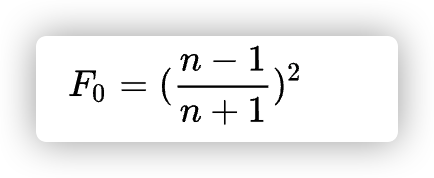
//原始F0求法
inline float3 FresnelF0_IOR(float IOR1, float IOR2)
{
float IOROffset = IOR2 - IOR1;
float IORAdd = IOR2 + IOR1;
IORAdd = IORAdd >0?IORAdd:0.001;
return Pow2(IOROffset / IORAdd);
}
inline float3 FresnelF0_IOR(float IOR2)
{
float IOROffset = IOR2 - 1;
float IORAdd = IOR2 + 1;
return Pow2(IOROffset / IORAdd);
}
有了F0,我们接下来就可以选则不同的菲尼尔算法来执行计算, 我们选取的法制包括了性能, 和接下来的法线分布、几何分布以及整体的统一性做衡量.
(这里额外说明 : 菲涅尔反射效应,和我们用来做一些效果的菲涅尔效果不要搞混淆,虽然在含义有类似部分, 其中菲涅尔效果等额外效果会在后面节点统一),
以下是一些实现: 这里注意下传入的是VH, 原因可以Google
inline float3 BaseFresnelSchlick(float HdotV, float3 F0)
{
return F0 + (1 - F0) * Pow5(1 - HdotV);
}
inline half3 FresnelLerp (half3 F0, half3 F90, half cosA)
{
half t = Pow5 (1 - cosA); // ala Schlick interpoliation
return lerp (F0, F90, t);
}
inline half3 FresnelLerpFast (half3 F0, half3 F90, half cosA)
{
half t = Pow4 (1 - cosA);
return lerp (F0, F90, t);
}
以及在间接光部分用的
inline float3 FresnelSchlickRoughness(float cosTheta, float3 F0, float roughness)
{
return F0 + (max(float3(1, 1, 1) * (1 - roughness), F0) - F0) * pow(1.0 - cosTheta, 5.0);
}
以及迪士尼
//传入某个角度的f,得到漫反射的1-f
inline float DSL_SchlickFresnel(float f)
{
float fd = clamp(1-f, 0, 1);
return Pow5(fd);
}
//漫反射的菲尼尔系数。
//没有次表面散射时,我们的F90:掠射角0.5, 垂直角度1
//并且基于粗糙度插值
inline float Fd_burley (float NdotL, float NdotV, float LdotH, float roughness){
float FL= DSL_SchlickFresnel(NdotL);
//F0时,NdotV=1. FV=0 Lerp(1, Fd90, FV) =1
//F90时,NdotV=0. FV=1 Lerp(1, Fd90, FV) =0
float FV= DSL_SchlickFresnel(NdotV);
float Fd90 = 0.5 + 2.0 * LdotH*LdotH * roughness;
return lerp(1, Fd90, FL) * lerp(1, Fd90, FV);
}
3 漫反射
这里选取了DiffR= Diff/PI,当然也有其他公式, 限于篇幅, 这些放在后续单独的章节实现总结.
这里我们假定用最Easy的方式 : diffcuseResult = pBRDF.diffuse. 然后进行KD衰减.
float3 diffcuseResult = Kd * pBRDF.diffuse / PI;
//DSL
float FD90 = 0.5 + 2 * VoH * VoH * Roughness;
float FdV = 1 + (FD90 - 1) * Pow5( 1 - NoV );
float FdL = 1 + (FD90 - 1) * Pow5( 1 - NoL );
return DiffuseColor * ( (1 / PI) * FdV * FdL );
4 镜面反射
NDF:法线分布函数,(这里我们先实现各向同性部分)
a\这个函数让材质有了亚像素级更精细的把控和更科学的定量, 是一种近似拟合. 通过BRDF进行建模,由粗糙度贴图(Roughness Map)配合法线分布函数,提供每亚像素(subpixel)法线信息
b\我们使用半矢量h来表示微观表面法线m,因为仅m = h的表面点的朝向才会将光线l反射到视线v的方向,其他朝向的表面点对BRDF没有贡献(正负相互抵消)
同时出现许多变化: 基本分为形状可变,不变.
这是一个合法的法线分布函数应该具备的特性

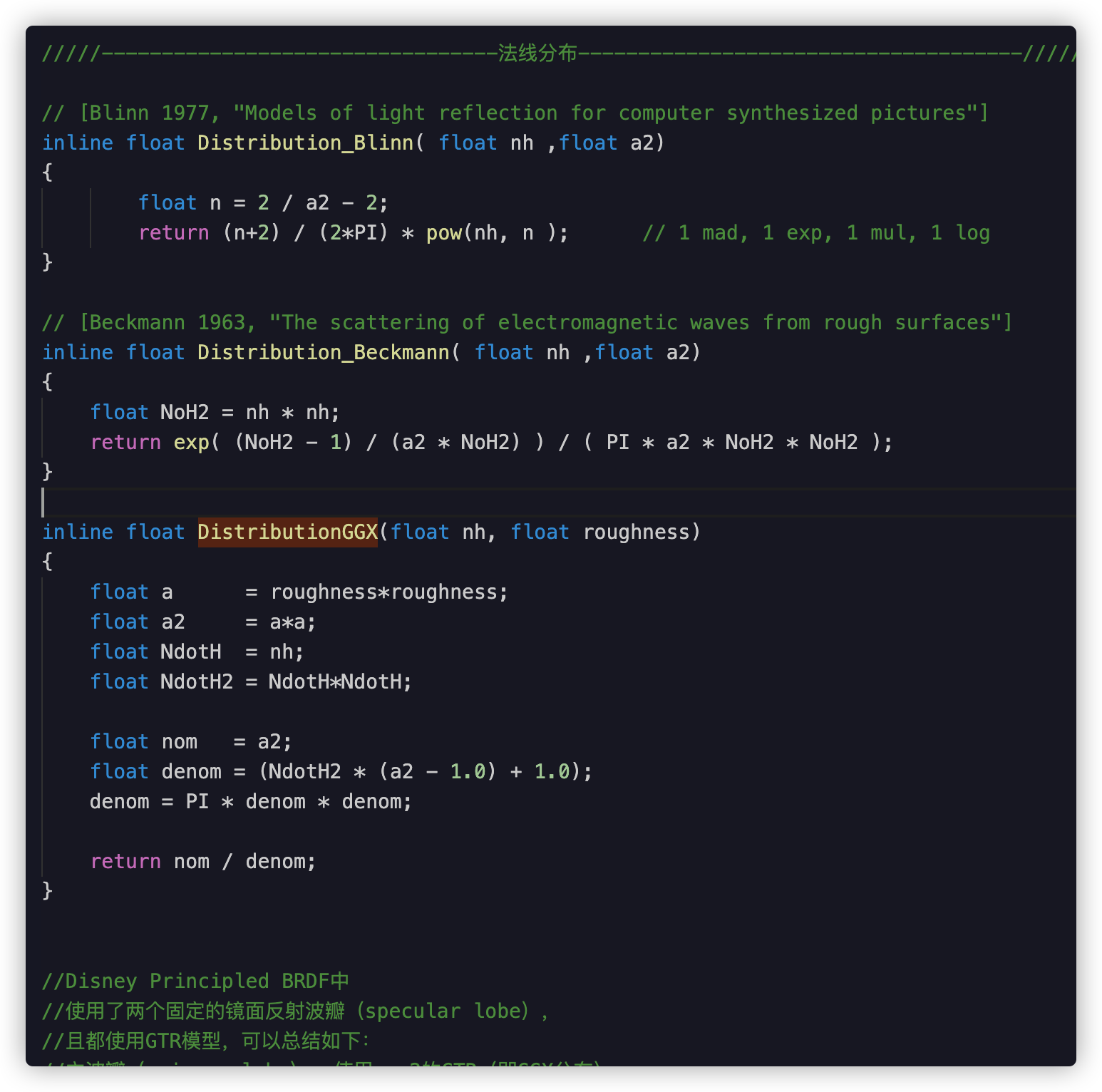
总结和推导法线分布函数
Cook Beckmann
// [Beckmann 1963, "The scattering of electromagnetic waves from rough surfaces"]
// src= exp(−tan2(α)/m2) 除以 πm2 cos4(α), 其中 α=arccos(n⋅h) m=a
// 其中−tan2(α) ===> -(1-cos2(α))/cos2(α) =>(cos2(α)-1)/cos2(α)>(nh2-1)/nh2
inline float Distribution_Beckmann(float a2, float nh)
{
float NoH2 = nh * nh;
return exp( (NoH2 - 1) / (a2 * NoH2) ) / ( PI * a2 * NoH2 * NoH2 );
}
G:几何函数:遮蔽+阴影
在基于物理的渲染中,几何函数(Geometry Function)是一个0到1之间的标量,描述了微平面自阴影的属性,表示了具有半矢量法线的微平面(microfacet)中,同时被入射方向和反射方向可见(没有被遮挡的)的比例,即
未被遮挡的m= h微表面的百分比
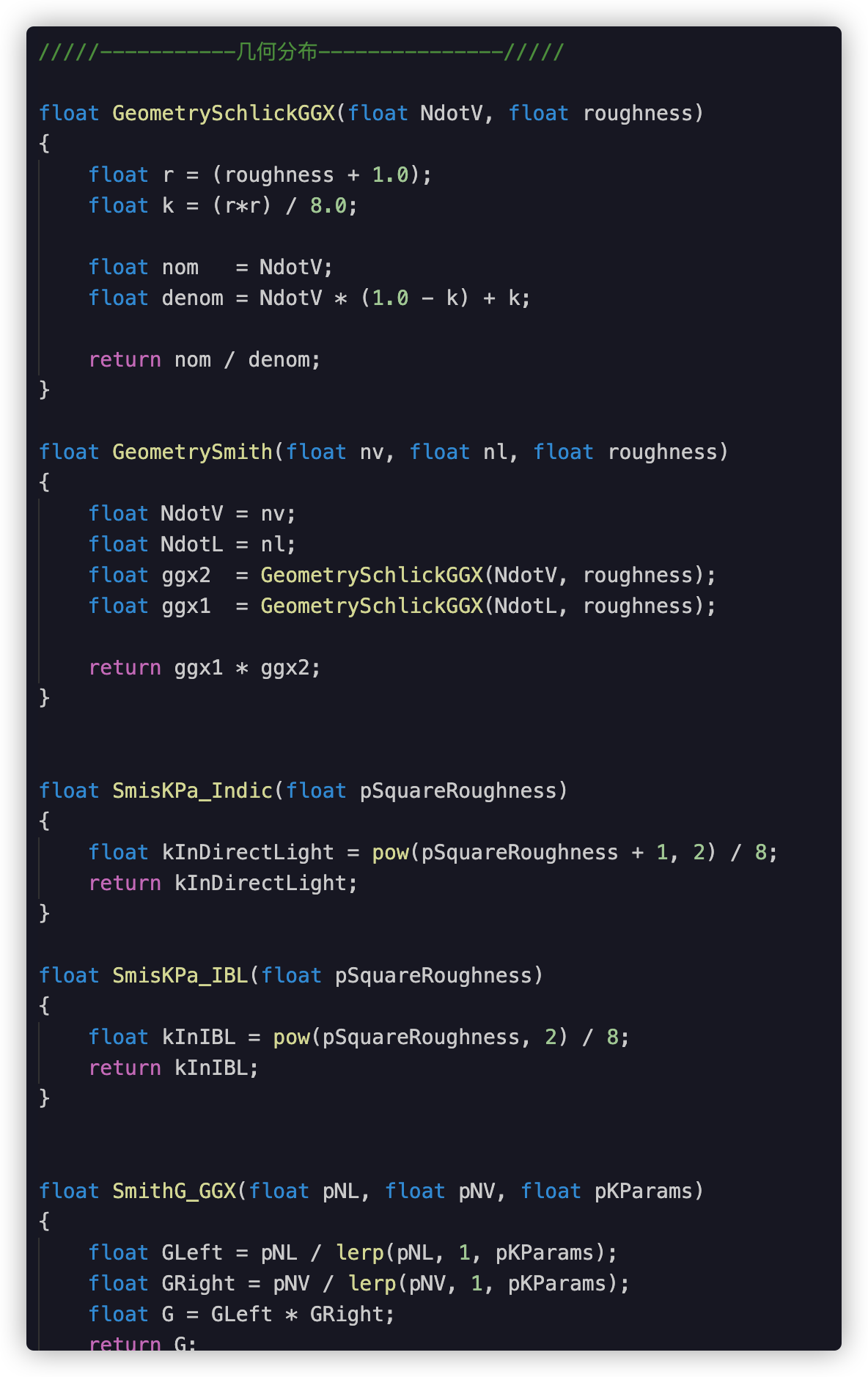
The Visibility Term
其中,在部分游戏引擎和文献中,几何函数G(l,v,h)和分母中的校正因子4(n·l)(n·v)会合并为可见性项(The Visibility Term),Vis项,简称V项
Unity(默认Render)和Unreal
Unity:
UnityStandardBRDF(感兴趣可以去看下这片Paper)
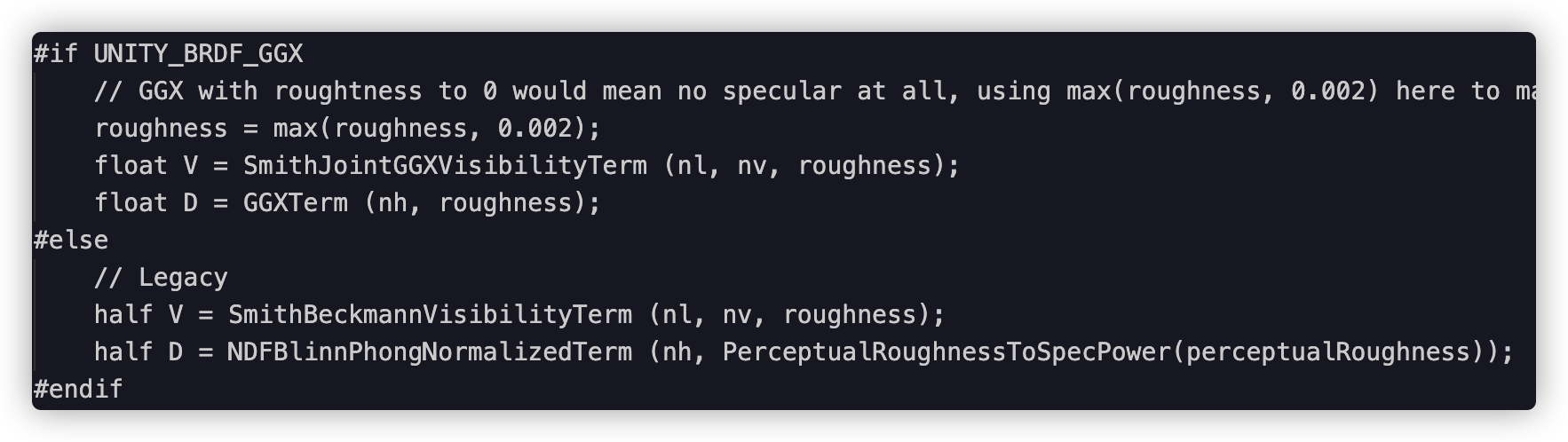
// Ref: http://jcgt.org/published/0003/02/03/paper.pdf
inline float SmithJointGGXVisibilityTerm (float NdotL, float NdotV, float roughness)
{
#if 0
// Original formulation:
// lambda_v = (-1 + sqrt(a2 * (1 - NdotL2) / NdotL2 + 1)) * 0.5f;
// lambda_l = (-1 + sqrt(a2 * (1 - NdotV2) / NdotV2 + 1)) * 0.5f;
// G = 1 / (1 + lambda_v + lambda_l);
// Reorder code to be more optimal
half a = roughness;
half a2 = a * a;
half lambdaV = NdotL * sqrt((-NdotV * a2 + NdotV) * NdotV + a2);
half lambdaL = NdotV * sqrt((-NdotL * a2 + NdotL) * NdotL + a2);
// Simplify visibility term: (2.0f * NdotL * NdotV) / ((4.0f * NdotL * NdotV) * (lambda_v + lambda_l + 1e-5f));
return 0.5f / (lambdaV + lambdaL + 1e-5f); // This function is not intended to be running on Mobile,
// therefore epsilon is smaller than can be represented by half
#else
// Approximation of the above formulation (simplify the sqrt, not mathematically correct but close enough)
float a = roughness;
float lambdaV = NdotL * (NdotV * (1 - a) + a);
float lambdaL = NdotV * (NdotL * (1 - a) + a);
#if defined(SHADER_API_SWITCH)
return 0.5f / (lambdaV + lambdaL + 1e-4f); // work-around against hlslcc rounding error
#else
return 0.5f / (lambdaV + lambdaL + 1e-5f);
#endif
#endif
}
Unreal:
这里我们注意一下,(引用:https://zhuanlan.zhihu.com/p/81708753)
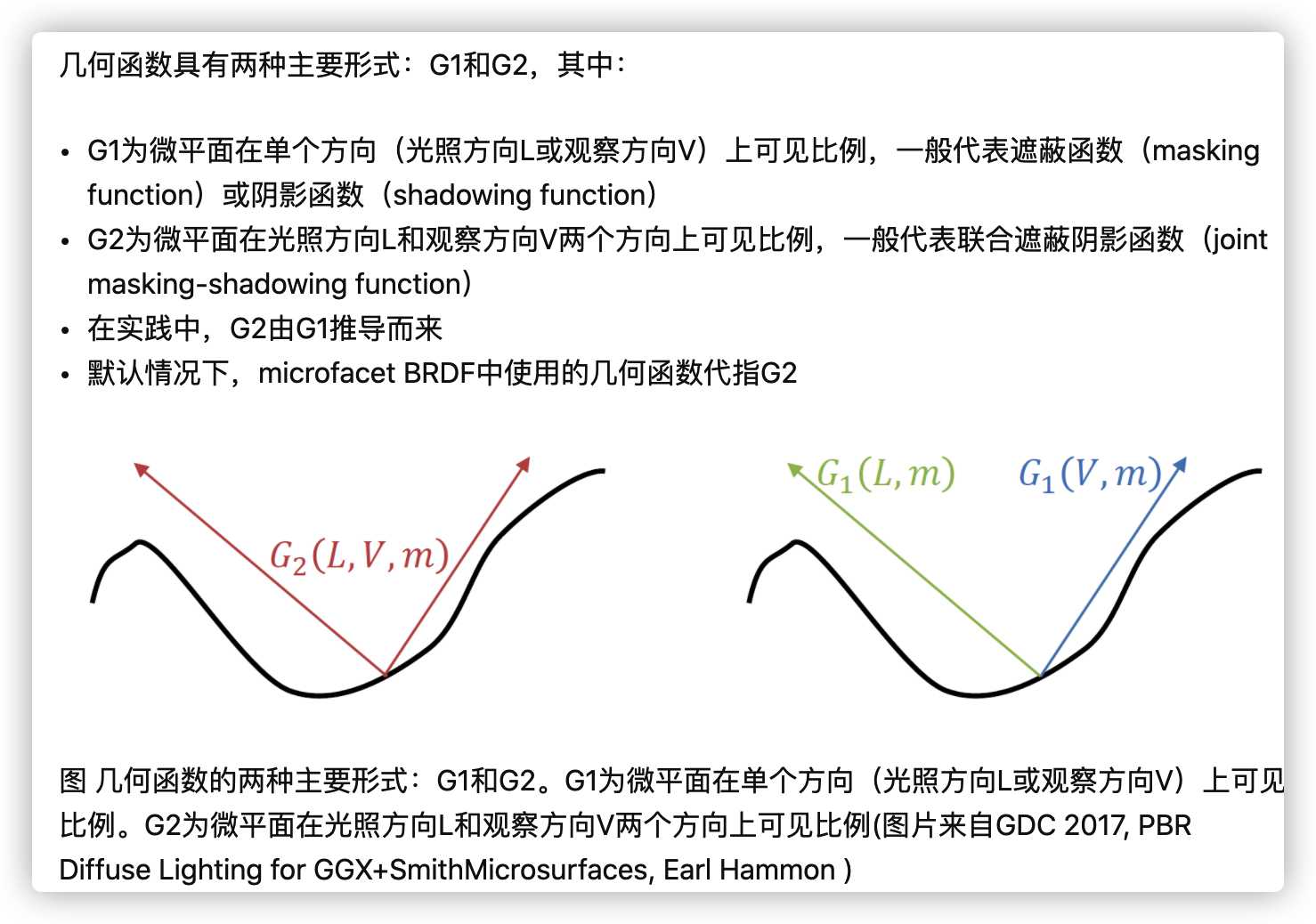
最后总结: 可以根据拟合程度选取.或近似实现. 这里要求选择合适的微表面轮廓(microsurface profile),从而对G项进行具象化建模。但G对BRDF的整体影响不大,但能保证能量守恒,在我们不断的分化过程会出现一定的比重.
具有相同法线分布但具有不同轮廓(profiles)的微表面导致不同的BRDF
-
分离的遮蔽阴影型(Separable Masking and Shadowing)
-
高度相关的遮蔽阴影型(Height-Correlated Masking and Shadowing)
-
方向相关的遮蔽阴影型(Direction-Correlated Masking and Shadowing)
-
高度-方向相关遮蔽阴影型(Height-Direction-Correlated Masking and Shadowing)
基本要求
- 标量性
- 对称性
- 同向可见性
- 拉伸不变性(Stretch Invariance)
最后给出一个测试的方法:
https://github.com/knarkowicz/FurnaceTest, 这部分会在接下来的HLSLLightFunction去实现,
F: 相对的菲涅尔反射方程结果
最后我们简单的实现一下
//法线分布: Input nh
float NDF = DistributionGGX(nh, pBRDF.roughness);
//几何: Input Nv, NL
float G = GeometrySmith(nv, nl, pBRDF.roughness);
float3 nominator = NDF * G * F;
float denominator = 4.0 * nv * nl + 0.001;
float3 specular = nominator / denominator;
5 积分部分
微表面模型的半球积分, 这里其实会涉及到蒙特卡洛积分(离散方式计算积分,概率搞一搞)
float3 DirectLightResult = (kD * diffcuseResult + specular) * lightColor * nl;
6 线性空间
还原现实世界方式的光与物质的交互的方式, 其中详细的颜色空间部分在后续说明.
1、我们输入的BaseColor(Diff), 金属度, 粗糙度需要转化到线性空间下, 保证后续的计算全部在线性空间.
2、完成后,需要再次将结果返回到伽马空间, 这里不一定是立马(关键看我们的Pipeline)
7 色调映射
Toonmap: 通过算法,将大于1的部分分散开来, 这样可以保证过亮部分得以在视觉上保留.(具体同理在后续)
8 对部分特性的处理
(具体同理在后续)
三、说明
这里梳理一下相关文件结构
XDArt_RenderLightFunction.hlsl: 函数库
XDArt_RenderLight_BRDF.hlsl : BRDF多个实现,BRDF输入结构定义
XDArt_RenderLight_BSSRDF.hlsl: BSSRDF多个实现,BSSRDF输入结构定义
XDArt_ShaderMode_DefaultLit.hlsl: 内置的多个LitMode实现
接下来就是具体使用, 和扩展
XDArt_ShaderMode_DefaultLit.shader
XDArt_ShaderMode_DefaultLit_RoughAO.shader
XDArt_ShaderMode_DefaultLit_Rough.shader
XDArt_ShaderMode_ClearCoat/Fab/Skin/Mon.shader.......等等



