Super max calculator(v2.0)

超级计算器2.0版本发布了

没想到第一次更新就更新了一个大版本。
图片预览：

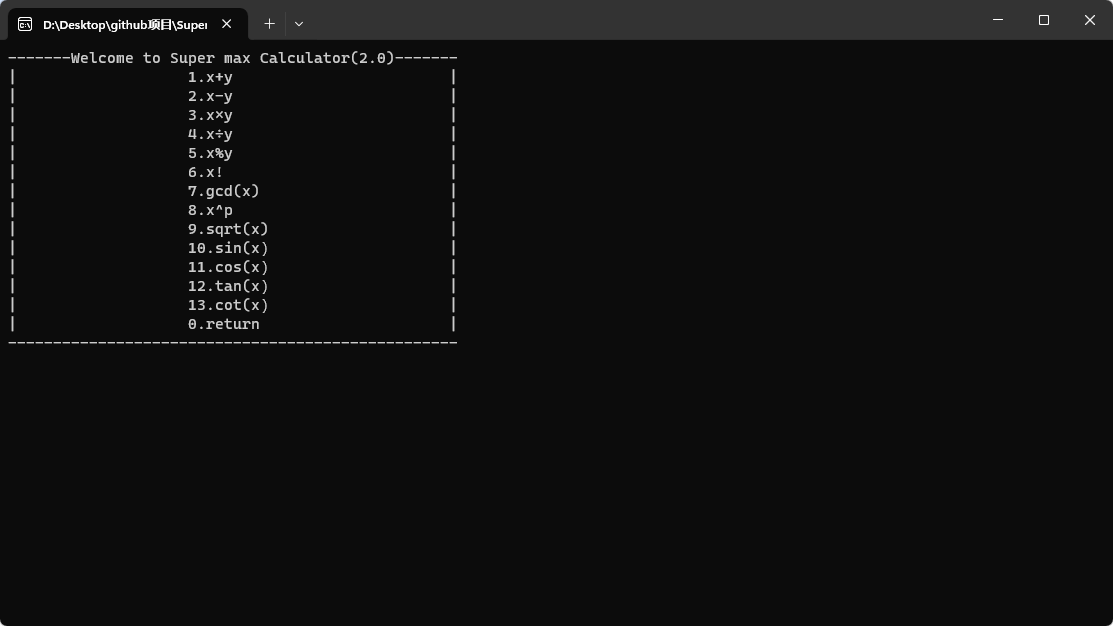
UI界面大改，新增了sin，cos等三角函数，并提供了一个程序可以运算多次结果的方法。
已在github上发布，
目前仅支持windows操作系统。
网址链接

源代码

/*
  Document name:Super max calculator(1.0)
  Language:Chinese
  Creator:Qiaochu Guo
 */
#include <bits/stdc++.h>
#include <windows.h>
using namespace std;
const int L=100005;
#define L(x) (1 << (x))
const double PI = 3.1415926;
const int Maxn = 133015;
double ax[Maxn], ay[Maxn], bx[Maxn], by[Maxn];
char sa[Maxn / 2], sb[Maxn / 2];
int sum[Maxn];
int x1[Maxn], x2[Maxn];
int revv(int x, int bits)
{
	int ret = 0;
	for (int i = 0; i < bits; i++)
	{
		ret <<= 1;
		ret |= x & 1;
		x >>= 1;
	}
	return ret;
}
void fft(double * a, double * b, int n, bool rev)
{
	int bits = 0;
	while (1 << bits < n) ++bits;
	for (int i = 0; i < n; i++)
	{
		int j = revv(i, bits);
		if (i < j)
			swap(a[i], a[j]), swap(b[i], b[j]);
	}
	for (int len = 2; len <= n; len <<= 1)
	{
		int half = len >> 1;
		double wmx = cos(2 * PI / len), wmy = sin(2 * PI / len);
		if (rev) wmy = -wmy;
		for (int i = 0; i < n; i += len)
		{
			double wx = 1, wy = 0;
			for (int j = 0; j < half; j++)
			{
				double cx = a[i + j], cy = b[i + j];
				double dx = a[i + j + half], dy = b[i + j + half];
				double ex = dx * wx - dy * wy, ey = dx * wy + dy * wx;
				a[i + j] = cx + ex, b[i + j] = cy + ey;
				a[i + j + half] = cx - ex, b[i + j + half] = cy - ey;
				double wnx = wx * wmx - wy * wmy, wny = wx * wmy + wy * wmx;
				wx = wnx, wy = wny;
			}
		}
	}
	if (rev)
	{
		for (int i = 0; i < n; i++)
			a[i] /= n, b[i] /= n;
	}
}
string mul(string a,string b)  
{  
	string s;  
	int na[L],nb[L],nc[L],La=a.size(),Lb=b.size();//na存储被乘数，nb存储乘数，nc存储积  
	fill(na,na+L,0);fill(nb,nb+L,0);fill(nc,nc+L,0);//将na,nb,nc都置为0  
	for(int i=La-1;i>=0;i--) na[La-i]=a[i]-'0';//将字符串表示的大整形数转成i整形数组表示的大整形数  
	for(int i=Lb-1;i>=0;i--) nb[Lb-i]=b[i]-'0';  
	for(int i=1;i<=La;i++)  
		for(int j=1;j<=Lb;j++)  
			nc[i+j-1]+=na[i]*nb[j];//a的第i位乘以b的第j位为积的第i+j-1位（先不考虑进位）  
	for(int i=1;i<=La+Lb;i++)  
		nc[i+1]+=nc[i]/10,nc[i]%=10;//统一处理进位  
	if(nc[La+Lb]) s+=nc[La+Lb]+'0';//判断第i+j位上的数字是不是0  
	for(int i=La+Lb-1;i>=1;i--)  
		s+=nc[i]+'0';//将整形数组转成字符串  
	return s;  
}  
int solve(int a[], int na, int b[], int nb, int ans[])
{
	int len = max(na, nb), ln;
	for (ln = 0; L(ln) < len; ++ln);
	len = L(++ln);
	for (int i = 0; i < len ; ++i)
	{
		if (i >= na) ax[i] = 0, ay[i] = 0;
		else ax[i] = a[i], ay[i] = 0;
	}
	fft(ax, ay, len, 0);
	for (int i = 0; i < len; ++i)
	{
		if (i >= nb) bx[i] = 0, by[i] = 0;
		else bx[i] = b[i], by[i] = 0;
	}
	fft(bx, by, len, 0);
	for (int i = 0; i < len; ++i)
	{
		double cx = ax[i] * bx[i] - ay[i] * by[i];
		double cy = ax[i] * by[i] + ay[i] * bx[i];
		ax[i] = cx, ay[i] = cy;
	}
	fft(ax, ay, len, 1);
	for (int i = 0; i < len; ++i)
		ans[i] = (int)(ax[i] + 0.5);
	return len;
}
string Pow(string a, int n)
{
	if (n == 1) return a;
	if (n & 1) return mul(Pow(a, n - 1), a);
	string ans = Pow(a, n / 2);
	return mul(ans, ans);
}
string fac(int n)
{
	int a[L];
	string ans;
	if (n == 0) return "1";
	fill(a, a + L, 0);
	int s = 0, m = n;
	while (m) a[++s] = m % 10, m /= 10;
	for (int i = n - 1; i >= 2; i--)
	{
		int w = 0;
		for (int j = 1; j <= s; j++) a[j] = a[j] * i + w, w = a[j] / 10, a[j] = a[j] % 10;
		while (w) a[++s] = w % 10, w /= 10;
	}
	while (!a[s]) s--;
	while (s >= 1) ans += a[s--] + '0';
	return ans;
}
string sub(string a, string b)
{
	string ans;
	int la = a.size();
	int lb = b.size();
	int lmax = max(la, lb);
	int na[L]={0},nb[L]={0}; 
	for (int i = 0; i < la; i++) na[la - 1 - i] = a[i] - '0';
	for (int i = 0; i < lb; i++) nb[lb - 1 - i] = b[i] - '0';
	for (int i = 0; i < lmax; i++)
	{
		na[i] -= nb[i];
		if (na[i] < 0) na[i] += 10, na[i + 1]--;
	}
	while (!na[--lmax] && lmax > 0)  lmax++;
	for (int i = lmax - 1; i >= 0; i--) ans += na[i] + '0';
	return ans;
}
string add(string a,string b)  
{  
	string ans;  
	int na[L]={0},nb[L]={0};  
	int la=a.size(),lb=b.size();  
	for(int i=0;i<la;i++) na[la-1-i]=a[i]-'0';  
	for(int i=0;i<lb;i++) nb[lb-1-i]=b[i]-'0';  
	int lmax=la>lb?la:lb;  
	for(int i=0;i<lmax;i++) na[i]+=nb[i],na[i+1]+=na[i]/10,na[i]%=10;  
	if(na[lmax]) lmax++;  
	for(int i=lmax-1;i>=0;i--) ans+=na[i]+'0';  
	return ans;  
}  

int sub(int *a,int *b,int La,int Lb)  
{  
	if(La<Lb) return -1;//如果a小于b，则返回-1  
	if(La==Lb)  
	{  
		for(int i=La-1;i>=0;i--)  
			if(a[i]>b[i]) break;  
		else if(a[i]<b[i]) return -1;//如果a小于b，则返回-1  
		
	}  
	for(int i=0;i<La;i++)//高精度减法  
	{  
		a[i]-=b[i];  
		if(a[i]<0) a[i]+=10,a[i+1]--;  
	}  
	for(int i=La-1;i>=0;i--)  
		if(a[i]) return i+1;//返回差的位数  
	return 0;//返回差的位数  
	
}  
string div(string n1,string n2,int nn)//n1,n2是字符串表示的被除数，除数,nn是选择返回商还是余数  
{  
	string s,v;//s存商,v存余数  
	int a[L],b[L],r[L],La=n1.size(),Lb=n2.size(),i,tp=La;//a，b是整形数组表示被除数，除数，tp保存被除数的长度  
	fill(a,a+L,0);fill(b,b+L,0);fill(r,r+L,0);//数组元素都置为0  
	for(i=La-1;i>=0;i--) a[La-1-i]=n1[i]-'0';  
	for(i=Lb-1;i>=0;i--) b[Lb-1-i]=n2[i]-'0';  
	if(La<Lb || (La==Lb && n1<n2)) {  
		//cout<<0<<endl;  
		return n1;}//如果a<b,则商为0，余数为被除数  
	int t=La-Lb;//除被数和除数的位数之差  
	for(int i=La-1;i>=0;i--)//将除数扩大10^t倍  
		if(i>=t) b[i]=b[i-t];  
	else b[i]=0;  
	Lb=La;  
	for(int j=0;j<=t;j++)  
	{  
		int temp;  
		while((temp=sub(a,b+j,La,Lb-j))>=0)//如果被除数比除数大继续减  
		{  
			La=temp;  
			r[t-j]++;  
		}  
	}  
	for(i=0;i<L-10;i++) r[i+1]+=r[i]/10,r[i]%=10;//统一处理进位  
	while(!r[i]) i--;//将整形数组表示的商转化成字符串表示的  
	while(i>=0) s+=r[i--]+'0';  
	//cout<<s<<endl;  
	i=tp;  
	while(!a[i]) i--;//将整形数组表示的余数转化成字符串表示的</span>  
	while(i>=0) v+=a[i--]+'0';  
	if(v.empty()) v="0";  
	//cout<<v<<endl;  
	if(nn==1) return s;  
	if(nn==2) return v;  
}
bool judge(string s)//判断s是否为全0串  
{  
	for(int i=0;i<s.size();i++)
		if(s[i]!='0')return false;  
	return true;  
}  
string gcd(string a,string b)//求最大公约数  
{  
	string t;  
	while(!judge(b))//如果余数不为0，继续除  
	{  
		t=a;//保存被除数的值  
		a=b;//用除数替换被除数  
		b=div(t,b,2);//用余数替换除数 
	}  
	return a;  
}  
double factorial(double n) {
	if (n <= 1) {
		return n;
	}
	else {
		return n * factorial(n - 1);
	}
}
double myabs(double num1)
{
	return((num1 > 0) ? num1 : -num1);
}
double snowsin(double num2)
{
	int i = 1, negation = 1;//取反
	double sum;
	double index = num2;//指数
	double Factorial = 1;//阶乘
	double TaylorExpansion = num2;//泰勒展开式求和
	do
	{
		Factorial = Factorial * ((__int64)i + 1) * ((__int64)i + 2);//求阶乘
		index *= num2 * num2;//求num2的次方
		negation = -negation;//每次循环取反
		sum = index / Factorial * negation;
		TaylorExpansion += sum;
		i += 2;
	} while (myabs(sum) > 1e-15);
	return(TaylorExpansion);
}

double snowcos(double x) {
	x = (PI / 2) - x;
	return sin(x);
}

double snowtan(double x) {
	return (snowsin(x) / snowcos(x));
}

double snowcot(double x) {
	return (1 / snowtan(x));
}
void cap()
{
	cout<<"-------Welcome to Super max Calculator(2.0)-------"<<endl;
	cout<<"|                   1.x+y                        |"<<endl;
	cout<<"|                   2.x-y                        |"<<endl;
	cout<<"|                   3.x×y                        |"<<endl;
	cout<<"|                   4.x÷y                        |"<<endl;
	cout<<"|                   5.x%y                        |"<<endl;
	cout<<"|                   6.x!                         |"<<endl;
	cout<<"|                   7.gcd(x)                     |"<<endl;
	cout<<"|                   8.x^p                        |"<<endl;
	cout<<"|                   9.sqrt(x)                    |"<<endl;
	cout<<"|                   10.sin(x）                   |"<<endl;
	cout<<"|                   11.cos(x）                   |"<<endl;
	cout<<"|                   12.tan(x）                   |"<<endl;
	cout<<"|                   13.cot(x）                   |"<<endl;
	cout<<"|                   0.return                     |"<<endl;
	cout<<"--------------------------------------------------"<<endl;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	while(1)
	{
		cap();
		int n;
		cin>>n;
		system("cls");
		string s,s1;
		int p;
		cap();
		if(n==0)
		{
			break;
		}
		if(n==6 or n==9 or n==10 or n==11 or n==12 or n==13)
		{
			cout<<"Please input x:"<<endl;
			cin>>p;
		}
		else if(n==8)
		{
			cout<<"Please input x:"<<endl;
			cin>>s;
			cout<<"Please input p:"<<endl;
			cin>>p;
		}
		else
		{
			cout<<"Please input x:"<<endl;
			cin>>s;
			cout<<"Please input y:"<<endl;
			cin>>s1;
		}
		system("cls");
		if(n==1)
		{
			cout<<s<<"+"<<s1<<"=";
			cout<<add(s,s1)<<endl;
		}
		else if(n==2)
		{
			cout<<s<<"-"<<s1<<"=";
			int la = s.size();
			int lb = s1.size();
			if(lb>la)
			{
				swap(s,s1);
				cout<<"-"<<sub(s,s1)<<endl;
				return 0;
			}
			cout << sub(s,s1)<<endl;
		}
		else if(n==3)
		{
			cout<<s<<"×"<<s1<<"=";
			cout << mul(s, s1)<<endl;
		}
		else if(n==4)
		{
			cout<<s<<"÷"<<s1<<"=";
			cout << div(s,s1,1)<<endl;
		}
		else if(n==5)
		{
			cout<<s<<"%"<<s1<<"=";
			cout << div(s,s1,2)<<endl;
		}
		else if(n==6)
		{
			cout <<p<<"!"<<"=";
			cout << fac(p)<<endl;
		}
		else if(n==7)
		{
			cout << "gcd("<<s<<","<<s1<<")"<<"=";
			cout << gcd(s,s1)<<endl;
		}
		else if(n==8)
		{
			cout << s << "^" << p <<"=";
			cout << Pow(s, p)<<endl;
		}
		else if(n==9)
		{
			cout<<"sqrt("<<p<<")"<<"=";
			cout << sqrt(p)<<endl;
		}
		else if(n==10)
		{
			cout<<"sin("<<p<<")"<<"=";
			cout<<snowsin(p * PI / 180.0)<<endl;
		}
		else if(n==11)
		{
			cout<<"cos("<<p<<")"<<"=";
			cout<<snowcos(p * PI / 180.0)<<endl;
		}
		else if(n==12)
		{
			cout<<"tan("<<p<<")"<<"=";
			cout<<snowtan(p * PI / 180.0)<<endl;
		}
		else if(n==13)
		{
			cout<<"cot("<<p<<")"<<"=";
			cout<<snowcot(p * PI / 180.0)<<endl;
		}
		else
		{
			cout<<"Wrong input, please input again!"<<endl;
		}
	}
	cout << "Thank you for using!\nPress any key to exit.\n";
	return 0;
}

有需自取。

有想法或有建议的可以在评论区留言或私信我。

我会将您的鼎鼎大名放在下面和Github上

特别鸣谢

空荡荡的……