欧拉回路(Eulerian Path)
1.定义
如果图\(G\)(有向图或者无向图)中所有边一次仅且一次行遍所有顶点的通路称作欧拉通路。
如果图\(G\)中所有边一次仅且一次行遍所有顶点的回路称作欧拉回路。
具有欧拉回路的图成为欧拉图(简称\(E\)图)。具有欧拉通路但不具有欧拉回路的图成为半欧拉图。
顶点可以经过多次
画个图分辨一下：
- 欧拉通路：
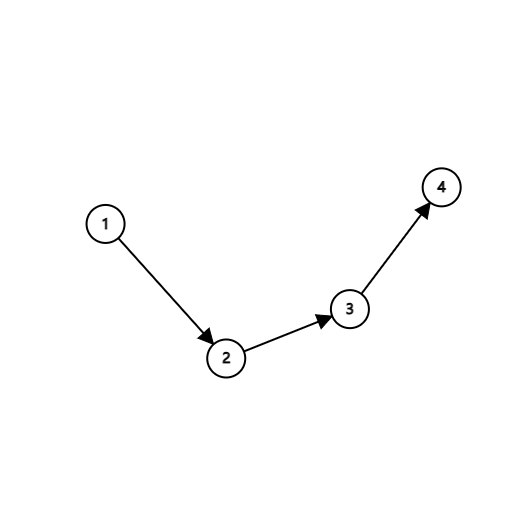
- 欧拉回路
简单来讲就是欧拉通路能够从起点到终点,欧拉回路能够回到起点
2.定理及推论
欧拉通路和欧拉回路的判定是很简单的
无向图\(G\)存在欧拉通路的充要条件是：
\(G\)为连通图，并且\(G\)仅有两个奇度节点(度数为奇数的顶点)或者无奇度节点
推论1：
- 当\(G\)是仅有两个奇度节点的连通图时，\(G\)的欧拉通路必以此两个节点为端点
- 当\(G\)是无奇度节点的连通图时，\(G\)必有欧拉回路
- \(G\)为欧拉图(存在欧拉回路)的充分必要条件是\(G\)为无奇度节点的连通图
有向图\(D\)存在欧拉通路的充要条件是：
\(D\)为有向图，\(D\)的基图联通，并且所有顶点的出度与入度都相等；或者除两个顶点外，其余顶点的出度与入度都相等，而在这两个顶点中一个顶点的出度与入度只为\(1\)，另一个顶点的出度与入度之差为\(−1\)
推论2：
- \(当D除出、入度之差为1，−1的两个顶点之外，其余顶点的出度与入度都相等时，D的有向欧拉通路必以出、入度之差为1的顶点作为始点，以出、入度之差为−1的顶点作为终点\)
- \(当D的所有顶点的出、入度都相等时，D中存在有向欧拉回路\)
- \(有向图D为有向欧拉图的充分必要条件是D的基图为连通图，并且所有的顶点的出、入度都相等\)
3.欧拉通路回路存在的判断
根据定理和推论，我们可以很好的找到欧拉通路回路的判断方法
A.判断欧拉通路是否存在的方法#
- \(有向图：图连通，有一个顶点出度大于入度1，有一个顶点入度大于出度1，其余都是出度=入度\)
- 无向图：图联通，只有两个顶点是奇数度，其余都是偶数度
B.判断欧拉回路是否存在的方法
- 有向图：图联通，所有的顶点出度=入度
- 无向图：图联通，所有的顶点都是偶数度
4.欧拉回路的应用
- 哥尼斯堡七桥问题
- 一笔画问题
- 旋转鼓轮的设计
5.欧拉回路的判断
\(DFS\)
邻接矩阵的时间复杂度为\(O(n^2)\)
邻接表的时间复杂度为\(O(n+e)\)
如果，重边太多的话，邻接表会挂掉:）
请看这篇文章
6.欧拉回路的求解
板子题：骑马修栅栏
传送门
题目保证有解。
A.DFS搜索求解欧拉回路
基本思路：利用欧拉定理判断出一个图存在欧拉回路或欧拉通路后，选择一个正确的起始顶点，用DFS算法遍历所有的边(每条边只遍历一次)，遇到走不通就回退。在搜索前进方向上将遍历过的边按顺序记录下来。这组边的排列就组成了一条欧拉通路或回路。
#include <bits/stdc++.h>
using namespace std;
int bian[510],n,m,ans[510];
int mapp[510][510],c=0;
void dfs(int j){
for(int i=1;i<=n;i++){
if(mapp[j][i]>0){
mapp[i][j]--;mapp[j][i]--;
dfs(i);
}
}
ans[c++]=j;
}
int main(){
cin>>m;
int a,b;
for(int i=0;i<m;i++){
cin>>a>>b;
mapp[a][b]++;mapp[b][a]++;
bian[a]++;bian[b]++;
n=a>n?a:n;
n=b>n?b:n;
}
int flag=1;
for(int i=n;i>=1;i--){
if(bian[i]%2==1){
flag=i;
}
}
dfs(flag);
for(int i=c-1;i>=0;i--){
cout<<ans[i]<<endl;
}
}
B.Fleury(佛罗莱)算法
- Fleury算法是对DFS爆搜的一种改进，使用DFS漫不经心的随意走效率是不高的，Fleury是一种有效的算法
ps:其实我也不会,这里就只介绍一下吧
我个人感觉是把大连通块分成了零散的几个小连通块然后分块连接
关键是能不走桥就不走桥，实在无路可走了才会去走桥
代码就不给了,估计给了也是错的
