数学笔记(2)-根式及其运算
调和平均 \(\leq\) 几何平均 \(\leq\) 算数平均 > \(\leq\) 平方平均
\(\frac {2}{\frac {1}{a}+\frac {1}{b}} \leq \sqrt{ab} \leq \frac {a+b}{2} \leq \sqrt{ \frac {a^2+b^2}{2}}\)
\(\sqrt{\frac{ab+\frac{1}{2}(a^2+b^2)}{2}}=\frac{1}{2}\)根式,是数学的基本概念之一,是一种含有开方(求方根)运算的代数式,即含有根号的表达式。按根指数是偶数还是奇数,根式分别称为偶次根式或奇次根式,零次根号几无意义。
根式的性质
运算法则
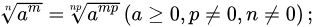

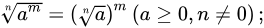
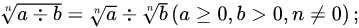
 ,其中
,其中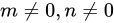
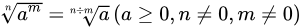
最简根式的定义
当根式满足以下三个条件时,称为最简根式。
- 被开方数的指数与根指数互质;
- 被开方数不含分母,即被开方数中因数是整数,因式是整式;
- 被开方数中不含开得尽方的因数或因式。
根式有理化
在进行二次根式计算时,一般通过找有理化因式的方法化去分母中的根号,常用方法为凑出平方差公式,如:
\((\sqrt a +\sqrt b)(\sqrt a -\sqrt b)=a-b\)
\(\frac{k}{\sqrt{n}+\sqrt{n-k}}=\sqrt n-\sqrt{n-k}\)
例题
\(\frac{2}{\sqrt 5 +\sqrt 3}\)
= \(\frac{2(\sqrt 5 -\sqrt 3)}{(\sqrt5 +\sqrt 3)(\sqrt 5 -\sqrt 3)}\)
= \(\frac{2(\sqrt 5 -\sqrt 3)}{2}\)
= \(\sqrt 5 -\sqrt 3\)


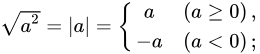
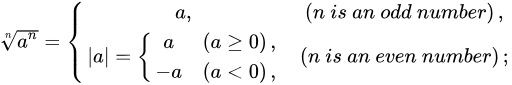
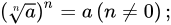
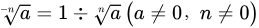



 浙公网安备 33010602011771号
浙公网安备 33010602011771号