寒假day4 2.5
讲师:钟皓曦,NOI2012Au,from 成都七中
dp
树形dp
核心:在树上做的 dp
给定一棵 \(n\) 个点的树,求这棵树有几个点。
对于树形 dp,第一个维度是 \(f_i\),代表以 \(i\) 为根的子树内的信息(有几个点)
树形 dp 的转移方法是把所有儿子信息整合
所有儿子的 dp 值 \(\rightarrow\) 自己。
转移:\(f_i=f_{son1}+f_{son2}+\ldots +f_{son_n}+1\)
答案:\(f_1\)
树形dp利用dfs实现
给定一棵 \(n\) 个点的树,每条边有边权,定义 \(dist(i,j)\) 代表 \(i\rightarrow j\) 的路径长度,求 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^ndist(i,j)\),数据范围 1e6。
\(f_i\) 代表 \(i\) 这棵子树内的答案。
考虑一条边被经过几次。什么时候会经过这条边?显然,\(i,j\) 一定要一个在外面,一个在里面。
令 \(f_i\) 代表子树大小,一条边连接 \(i\) 与其父亲的边被经过的次数就是 \(2\times f_i\times (n-f_i)\)。(乘法原理)
注意两个点可以换顺序,所以应 \(\times 2\)。
给定一棵 \(n\) 个点的树,有边权,求 \(max_{i,j}dist_{i,j}\),1e6。
其实是求树的直径。
如果边权非负,两点一定都是叶子节点。
令 \(f_i\) 代表子树内**距离 \(i\) **最远的距离,\(g_i\) 代表次远的距离。
树上路径组成:起点+终点+LCA
答案:\(\max_{1\le i\le n}(f_i+g_i)\),这里做的是枚举 LCA。
如何考虑转移?
画一个数轴,观察当前值 dis 与 \(f_{now}\) \(g_{now}\) 的位置关系。
求树的最大独立集,没有上司的舞会。
最大独立集:选出尽量多的点,使得它们不相邻。
把根节点染成黑色,子节点染成异色,不断染,统计黑白数量,这是错误的,但告诉我们树是二分图。
证明一件事错误是很困难的,但举出反例是容易的
令 \(f_i\) 代表子树内根节点染色的情况下最大独立集,\(g_i\) 代表不染色的情况下最大独立集。
发现 \(i\) 是否染色,会根据儿子是否染色。
dp中可以把所有想知道的事记到状态里
考虑 \(f_i\) 的转移。
此时儿子肯定都不能选,\(f_i=1+\sum\limits_{k=1}^mg_{son_k}\)
对于 \(g_i\),儿子可选可不选,所以 \(g_i=\sum\limits_{k=1}^m\max(f_{son_k},g_{son_k})\)
ppt 41 P5 poj463
利用上一题的思想。令 \(f_i\) 代表没有士兵,由儿子守护。
对于 \(i\) 点,如果不放士兵,所以要不是儿子保护它,要不然就是父亲守护它,增加 \(h_i\) 代表没有士兵,但是由父亲守护。
对于 \(f_i\) ,至少一个儿子要有士兵。
令 \(p_{i,0/1}\) 代表前 \(i\) 个儿子,是否有士兵,————————————。
建议看代码,讲的有点快。
树形dp常见手段——将所有儿子信息合并时,往往需要另一个dp辅助合并
\(f_i=\sum\limits_{k=1}^m\)
\(g_i=1+\sum\limits_{k=1}^m\min(f_{son_k},g_{son_k},h_{son_k})\)
\(h_i=\sum\limits^mf_k\)
状压dp
核心思路:把 \(n\) 个数压缩成一个数
二进制状态压缩——只有 0/1 两种取值
ppt 60 P1 吃奶酪
用 \(n\) 位的二进制数表示每个点是否走过,这个二进制数 \(\le 2^n\)。
令 \(f_{S,i}\) 代表每个点状态集合为 \(S\) 时终点是 \(i\) 的情况下的最小距离。
初始化:一开始把所有值标记成 double_inf ,\(f_{1,0}=0\)
判断集合中的状态:i&(1<<j)
合并状态:chkmin(f_{1|(1<<k),k},f_{i,j}+dis_{j,k})
把 bool 数组变成一个数
注意最后加答案要走回 \(0\) 号点。
复杂度 \(O(2^N\times N^2)\)
状压的题范围不会很大 \(\rightarrow\) 范围不是很大的题可能会是状压。
ppt 61 P2 P1879
一个格子能不能种草:上一行种没种,这一行有没有相邻的种草。
\(f_{i,j}\) 表示前 \(i\) 行已经种好草,第 \(i\) 行的种草情况为 \(j\) 时的方案数。
枚举下一行的种草情况,统计方案数。
K 国王问题 P1896
与上题的不同——国王数量
多一个条件 \(\rightarrow\) 加一个维度
\(f_{i,j,k}\) 代表前 \(i\) 行种草情况为 \(j\) ,已经用了 \(k\) 个国王的方案数。
剩下一致。
ppt 118 P6 CodeChef LEMOUSE
令 \(f_{i,j}\) 代表走到 \((i,j)\) 最少老鼠数。
经典题,方格取数。
但是显然不对。
令 \(f_{i,j,0/1,0/1}\) 代表走到 \((i,j)\) 时,上一步是向右/下,上两步向右/下走。
考虑到被同一只老鼠反复吓到中间过程最多走两步。
复杂度 \(O(4n^2)\)
ppt 124 P9 P2051
放炮要规定一个顺序——一行一行放
讨厌计数题
令 \(f_{i,j,k}\) 代表放到第 \(i\) 行时,有 \(j\) 列放了 \(0\) 个炮,有 \(k\) 列放了 \(1\) 个炮。
显然,有 \(m-j-k\) 列放了两个炮。
对于第 \(i\) 行,可以放 \(0\sim 2\) 个炮。
\(0:f_{i,j,k}+=f_{i-1,j,k}\)
\(1:f_{i,j,k-1}+=f_{i-1,j,k}\times k,f_{i,j-1,k+1}+=f_{i-1,j,k}\times j\)
对于放两个炮的情况,有三种情况进行转移。
博弈论dp
\(n\) 个点,\(M_{i,j}=0/1\) 代表 \(i\rightarrow j\) 是否右有边,求从 \(1\) 号点出发走 \(t\) 步到 \(n\) 号点的方案数。
怎么又是计数题
令 \(f_{i,j}\) 代表走了 \(i\) 步走到 \(j\) 的方案数。
\(M_{j,k}==1\rightarrow f_{i+1,k}+=f_{i,j}\)
时间复杂度 \(O(TN^2)\)
另一种写法:\(f_{i,j}=\sum\limits_{k=1}^Nf_{i-1,k}\times M{k,j}\)
范围 \(N\le 100,T\le 10^9\)
dp常见优化技巧:把二维变成三维后利用矩阵乘法优化
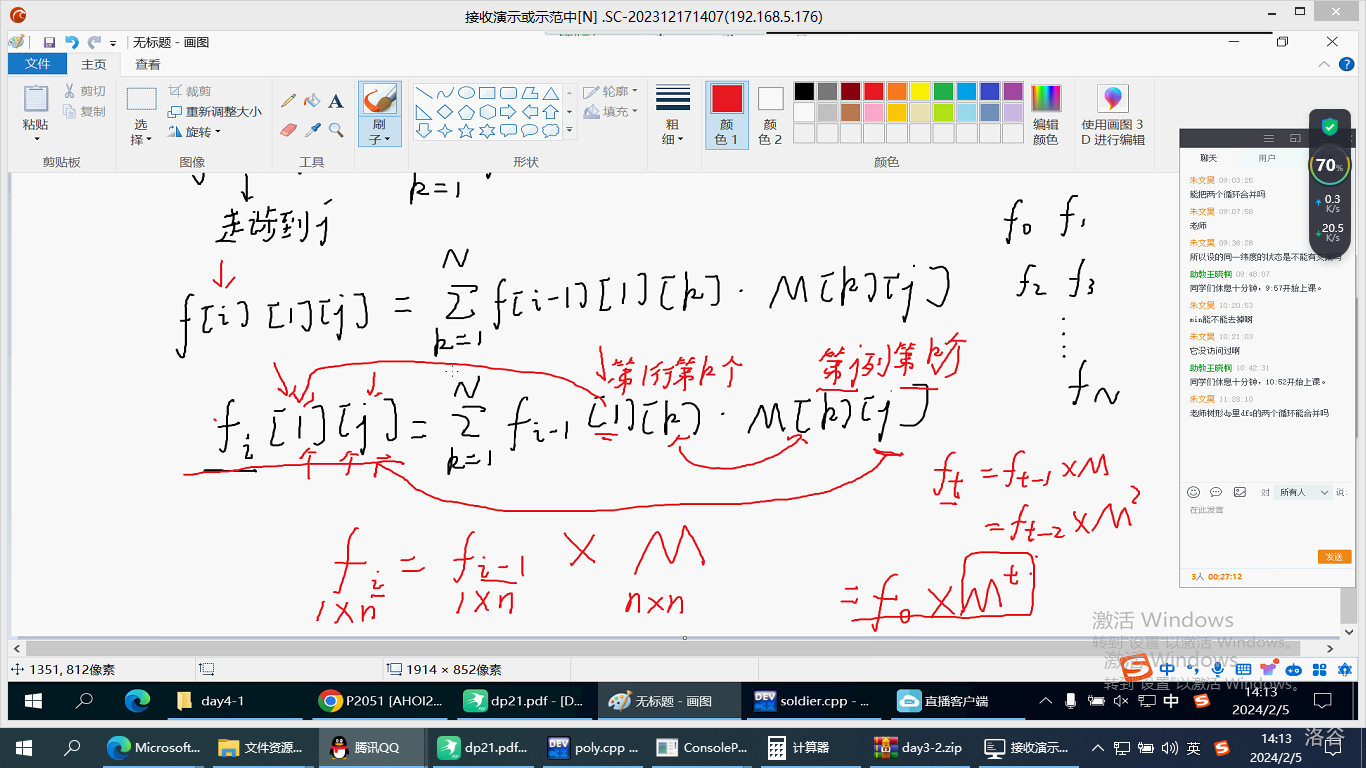
\(f_i[1][j]=\sum\limits_{k=1}^Nf_{i-1}[1][k]\times M[k][j]\)
发现 \(f_i=f_{i-1}\times M\)
复杂度 \(O(N^3\log T)\)
用矩阵乘法优化的 dp 题的特点:\(f_i\) 只和 \(f_{i-1}\) 有关;转移系数 \(M\) 与 \(i\) 无关。
复杂度:\(O(n^2\times t)\rightarrow O(n^3\log t)\)
迷路 P4159
本题的不同是存在边权——拆点。
但发现拆完以后存在 \(800\) 个点,会 T。
考虑删去一下无用的边。
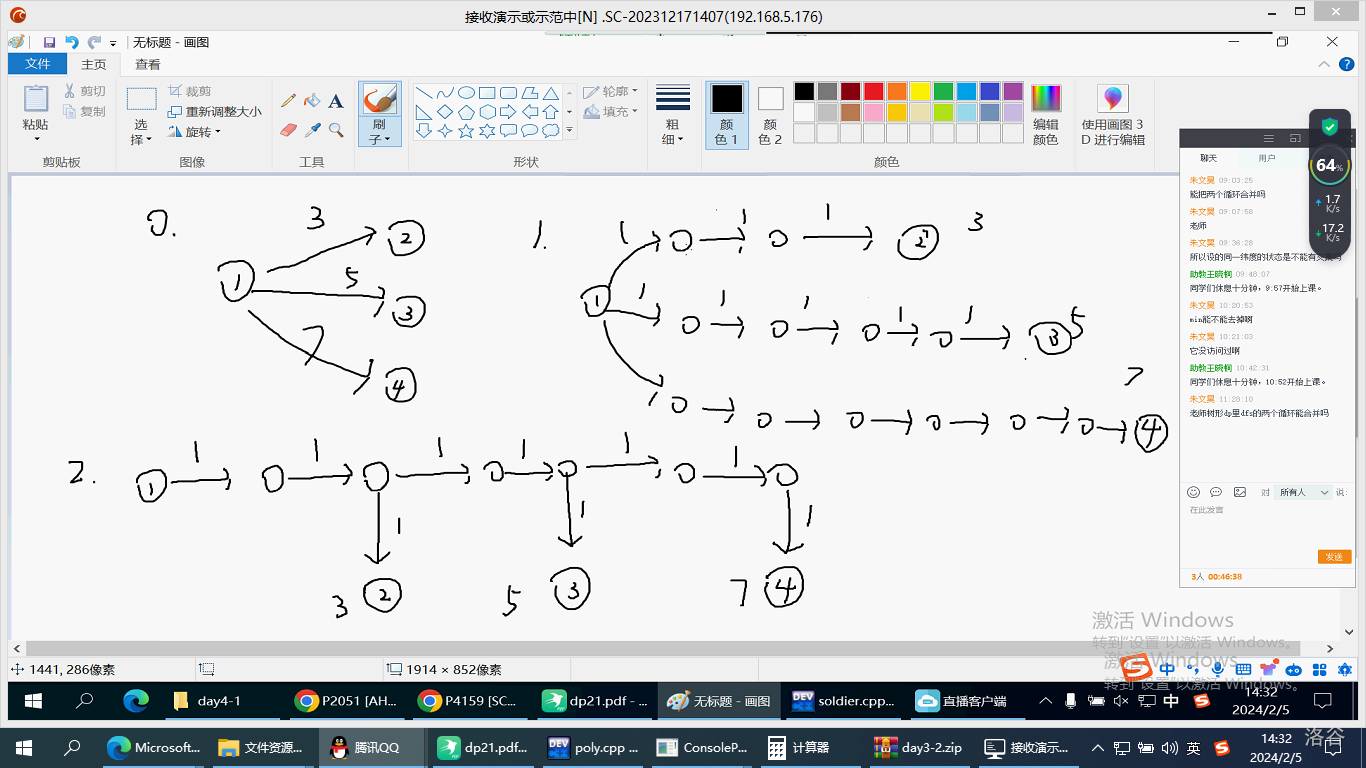
发现只有 \(9n\) 个点,可以接受。
有一张 \(n\) 个点的图,给出 \(T\),求从 \(1\) 号点走 \(T\) 步到 \(n\) 号点的方案数,\(M_{i,j}\) 表示从 \(i\) 到 \(j\) 有几条边,\(in_{i,j}\) 表示第 \(i\) 个点的第 \(j\) 个入度,给出 \(in_{i,j},out_{i,j}\),\(N\le 1000,T\le 10^9,r\le 20\)。BZOJ 3583
发现 dp 式子和前面题一样,可恶的计数题。
观察到 \(r\) 很奇怪,考虑把 \(r\) 作为突破口。
\(M_{i,j}=\sum\limits_{k=1}^rout{i,k}\times in_{j,k}\)
考虑在读入时更换 in 数组的第一个和第二个维度,看做矩乘。
\(M=out\times in\)
复杂度变成了 \(O(r^3\log T)\),总之很抽象。
发现三道题都是变成第一道题,所以要把未知问题变成已知问题。
博弈论dp
给定 \(N\) ,可以将其变为 \(N-1,N-2,N-4,N-8\),谁先变成 \(\le 0\) 谁输。
\(f_i\) 代表数为 \(i\) 时,先手必胜还是必败。
显然,\(f_{-7\sim 0}=1\),是先手的对手把 \(N\) 变成非法了,所以先手必胜。
考虑对 \(i\) 一次操作后的取值,设 \(f_{i-1}=T,f_{i-2}=F,f_{i-4}=T,f_{i-8}=T\),此时显然应该选择 \(i-2\),因为对手必败。
可以发现,所有能转移到的状态中如果存在必败态,则 \(i\) 为必胜态;否则 \(i\) 为必败态。
存在一步操作使得对手必败,则自己必胜;若所有操作使得对手必胜,则自己必败
能用记搜最好用记搜
状态=游戏的状态
表示当前状态是否必胜
转移根据规则操作
要看能否转移到必败态
\(S\),每次减去一个正整数,但不能超过上一轮减去的数的 \(k\) 倍,问必胜/必败。
\(f_{S,i}\),减去 \(i\)。
初始 \((x=1,y=0)\),操作:\((1,x+y),(2x,y),(3x,y)\),如果 \(x+y\ge n\) 只能用 \(1\),\(y\ge n\) 输。BZOJ 2798
令 \(f_{x,y}\) 代表两个数为 \((x,y)\) 时的先手状态。
根据规则转移。发现时空限制不可以,\(O(n^2)\)。
发现 \(x\) 一定可以表示成 \(2^{d1}\times 3^{d2}\),将状态变为 \(f_{a,b,y}\)。
\(n\) 个数,每个数 \(\le 100\),取数,取完 GCD 变成 1 就输。CodeChef Sereja ans Game
\(f_{i,j}\) 代表取了 \(i\) 个数,GCD 为 \(j\) 时的状态。
转移时,把 \(n\) 个数分为两类,是/不是 \(j\) 的倍数。
在不是倍数的那堆里,一定可以随便选。\(f_{i,j}\rightarrow f_{i+1,\gcd{j,c_k}}\)
另外一堆,随便选也都行(除非 \(i\ge m\))\(f_{i,j}\rightarrow f_{i+1,j}\)。
可以感性理解。
\(n\) 个数,每次可以把某一个数变为 \(x-1,x-2,x-4,x-8\),把 \(a_i\le 0\),输
SG 值:对于一个必败态的 SG 值,一定为 \(0\)。一个数 \(i\) 的 SG 值为 \(\operatorname{mex}{\operatorname{SG}(i-1),\operatorname{SG}(i-2),\operatorname{SG}(i-4),\operatorname{SG}(i-8)}\)
SG(1)=0
SG(2)=mex(SG(1))=1
SG(3)=mex(0,1)=2
SG(4)=mex(2,3)=0
求 \(\operatorname{mex}(z_0,z_1,z_2,\ldots,z_{m-1})\)
先排序,再去重,再用指针求 mex
z[m]=-1,sg[i]=0;
while(z[sg[i]]==sg[i])
sg[i]++;
return sg[i];
去重前一定要排序
SG(必败态)=0
SG(必胜态)不等于0
SG 定理:\(n\) 个游戏组合在一起的 SG 值,等于每个游戏的 SG 值异或起来
第一类博弈论:针对单个游戏,利用必胜/必败进行 dp
第二类博弈论:针对多个游戏,利用 SG值 进行 dp
Nim 石子游戏问题
选一堆石子,每次对一堆取走至少一个石子。
答案就是看 \(a_1\oplus a_2\oplus\ldots\oplus a_n\) 是否为 \(0\)。
所有第二类博弈论问题做法——用 SG值 进行dp or 转换为 Nim
ppt 78 P4
在长度为 \(i\) 的空格子中染第 \(j\) 个,发现 SG(i)=mex(SG(j-3)\(\oplus\) SG(i-j-2))
二类套二类。
ppt 82 P6
发现子游戏互相影响。
在博弈论中,如果操作可以被对手模仿,那这就是没有意义的
答案:\(a_1\oplus a_3\oplus a_5\ldots\) 是否为 \(0\)。
对于偶数层的石子,只要先手怎么移,后手就跟着怎么移。
对于奇数层的石子,搬一次后就没有意义了。
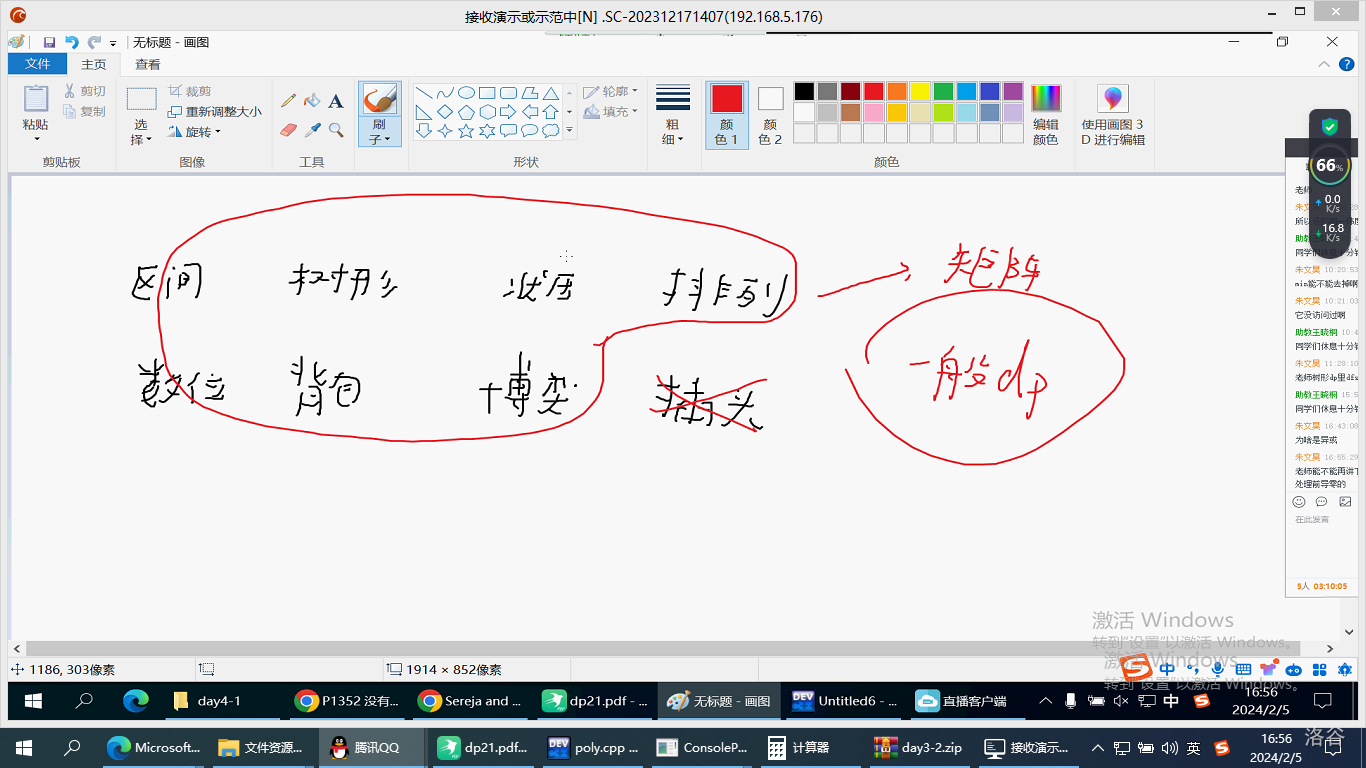
关键——状态的设计
最难的——看出这个题要 dp
网络流和 dp 非常容易混淆,两者都属于线性规划问题
状态设计套路——题目中什么量在变化




