寒假day3 2.4
讲师:钟皓曦,NOI2012Au,from 成都七中
听课能听懂 30% 就算成功
dp
关键:状态、转移、初始化
转移:状态与状态之间的关系
初始化:状态的边界条件
数字三角形
状态:\(f_{i,j}\) 表示走到 \(a_{i,j}\) 这个位置的最大价值。
如何设计状态?
题目要你干什么——从第一行走到最后一行
该过程中什么在变化——位置、价值
题目求什么——最大价值
一般情况下状态表示形式:\(f[\text{除题目所求外所有在变化的量}]=\text{题目所求}\)。
如果每次走还有能量的花费,怎么定义状态?
再加一维,表示能量(能量在变化)。
先不要管维度是不是太多,先扔进去
维度少了,是做不了题的;维度多了,可以慢慢删
数字三角形2 noip.ac 2106
设定基本类似,目标:使得经过的所有数之和 %100 之后最大。
考虑刚才的状态能不能做这道题。
显然不能。不满足最优子结构。
反例:
1
50 97
1
2
dp 本质上类似贪心。
发现做不了——维度不够。
维度从哪找——变化的量。
先不要关注时空限制,保证答案正确。
变化的量——位置、%100 之后的价值
状态:\(f[i][j][k]\) 表示走到 \((i,j)\) 这个位置是否能达到 \(k\) 的价值。
斐波那契数列
求 \(f_n\% (10^9+7)\),\(n\le 100\)。
有几种暴力写法?
两种——用别人更新自己(递推),用自己更新别人
dp 时要根据题目选择用哪一种。
比如,\(f(i)=\max\limits_{l\le j\le r}f_j+a_i\),只能用别人更新自己。
除了数据结构优化 dp 的题,大部分两种写法都可以。
第三种写法——记搜,博弈论dp中常用
f[n]=dfs(n-1)+dfs(n-2)
复杂度 \(O(f(n))\)。
从组成表示来理解。
利用记忆化优化,用 \(g_i\) 表示是否已经求出 \(f_i\)。
复杂度 \(O(n)\)。
\(g_i\) 只会有一次 \(0\rightarrow 1\)。
前置知识结束
对 dp 分类——背包、区间、树形、数位、状压、插头、排列、博弈、一般
除了一般 dp 外,都有固定的状态设计和转移方程的写法。
最难的——一般 dp,没有套路。
ppt 108 P1 HDU5009
发现对一个位置修改多次没有意义,并且先染左边和先染右边没有区别。
于是定义从左到右进行染色。
顺序在 dp 上很重要。
\(f_i\) 表示 \(1\sim i\) 全都染完色的最小代价。
\(f_i=\min\limits_{1\le j<i}(f_j+diff(j+1,i)^2)\)。
时间复杂度 \(O(n^2)\)。
\(ans\le n\)(一个一个改)。
换句话说,选择的区间中不同颜色数不能超过 \(\sqrt{n}\)。
即 \(diff(j+1,i)\le \sqrt{n}\)。
枚举 \(\sqrt{n}\) 个位置。
发现决策单调性。
用 \(\sqrt{n}\) 个双指针维护这 \(\sqrt{n}\) 个位置。
时间复杂度 \(O(n\sqrt{n})\)。
排列dp
指 \(1\sim n\) 的排列。
总共有 \(n!\) 种。
所有排列中,满足某个条件的 dp 称为排列 dp 。
\(1\sim n\) 的所有排列中逆序对个数为偶数的有多少个?
排列dp的转移方法:把所有数从小到大或从大到小一个一个插入。
状态:\(f_i\) 代表 \(i\) 已经被插入。
对于本题,变化的除了 \(i\) 还有逆序对个数。
\(f_{i,j},j\le \frac{i(i-1)}{2}\) 代表插入 \(i\) 后当前有 \(j\) 个逆序对的方案数。
设插入后为 \(a_1\ldots a_i\)。
将 \(i+1\) 可以插入的位置从 \(0\sim i\) 标号。
考虑插入将 \(i+1\) 插入到第 \(k\) 个位置,会增加 \(k\) 个逆序对。
\(f_{i+1,j+i-k}+=f_{i,j},1\le i<n,\le j\le\frac{i(i-1)}{2},0\le k\le i\)
用自己更新别人。
时间复杂度 \(O(n^4)\)。
考虑优化。题目只需要求偶数逆序对的个数,所以把 \(f_{i,j},0\le j\le 1\),代表奇偶性。
所以转移时枚举 \(j\) 时只需要枚举 \(0/1\)。
时间复杂度 \(O(n^2)\)。
答案是 \(\frac{n!}{2}\)。
方法:第一个维度代表已经插入 \(i\),转移方法:把所有数从小到大/从大到小插入,枚举插入的位置。
定义一个数在排列中激动代表比它前面的数都大,排列的激动值代表有多少个激动的数。求 \(1\sim n\) 排列中激动值为 \(k\) 有多少个。
codechef FEB 114 LEMOVIE
发现从小到大插入,如果插入 \(i+1\),可能会导致激动值减小。
所以从大到小插入。
\(f_{i,j}\) 代表已经把 \(n\sim i\) 插入,激动值为 \(j\) 的方案数。
发现只有当 \(i-1\) 插入到最前面时才会导致激动值+1,否则不变。
\(f_{i-1,j+1}+=f_{i,j}\),插入到最前面。
\(f_{i-1,j}+=f_{i,j}\times (n-i+1)\),不插入到最前面,还需要乘上方案数。
背包dp
采药 01背包
有 \(N\) 个物品,两个属性,价值 \(w_i\),体积 \(v_i\)。要放入一个容积为 \(M\) 的背包,求最大价值。
什么在变化——背包体积、背包价值、选到第几个物品
\(f[\text{第几个}][\text{体积}]=\text{价值}\)
表示前 \(i\) 个物品考虑完毕,用掉了 \(j\) 的体积,所能获得的最大价值。
对于每个物品——选 或 不选
选——\(f_{i,j}=f_{i-1,j-v_i}\)
不选——\(f_{i,j}=f_{i-1,j}\)
用别人更新自己。
如果 \(f_{i,j}=0\) 代表不存在这一种情况。
发现满足最优子结构。
01背包:只有两种可能性,选或不选
时间复杂度 \(O(nm)\)。
无穷背包/完全背包
每个物品有无数个。
考虑枚举第 \(i\) 种物品放几个。
\(f_{i,j}=\max(f_{i,j},f_{i-1,j-k\times v_i}+k\times w_i)\)
最坏时间复杂度 \(O(n^2m)\),\(n\) 与 \(m\) 同阶。
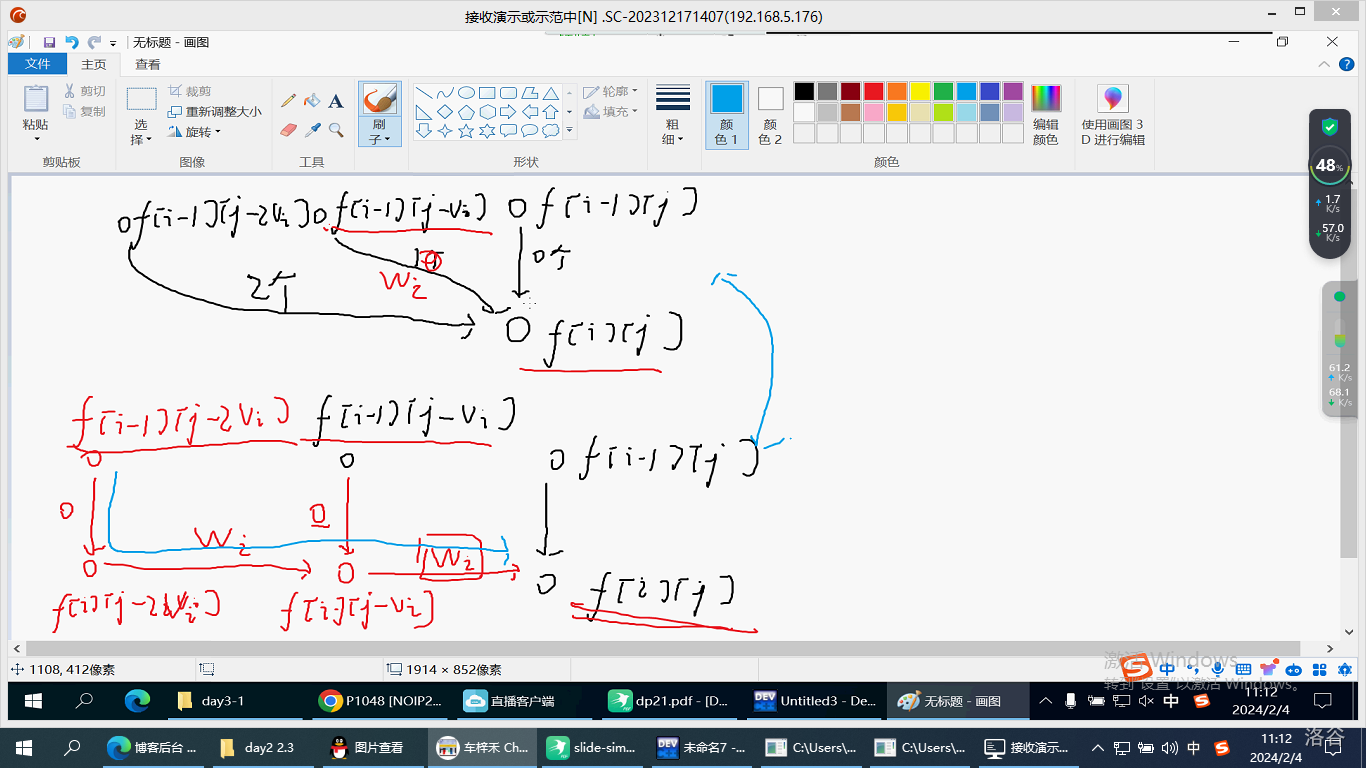
上图即为优化。竖着的箭头代表要开始选第 \(i\) 个,横着的箭头代表又选了一个。
更具体的解释。我们考虑 \(f_{i,j}\) 本质上就是要求在 \({i,j}\) 的情况下,价值的最大值。在 AcWing 的 dp 课程中,提到过 dp 本质上是状态的集合,指的就是 \({i,j}\) 在多种选择方法所构成的集合中价值最大的那一个,于是我们设这一个选择方案是 \(a_0\times num_0+a_1\times num_1\ldots a_i\times num_i\),其中 \(num_i\) 代表第 \(i\) 种选了 \(num_i\) 个。现在考虑关于第 \(i\) 种选几个的问题。假如说不选,自然就是从 \({i-1,j}\) 这个状态转移过来。如果选,我们只考虑要不要多选一个的问题,如果要多选一个,最优的转移方案一定是 选这一个之前最优的+这一个的价值,显然是 \(f_{i,j-v_i}+w_i\),因为根据刚才的“闫氏dp法”,我们发现 \(f_{i,j-v_i}\) 就是在第 \(i\) 种选了 \(num_i\) 个后体积达到 \(j-v_i\) 的最优方案,现在体积为 \(j\),多选一个之前的体积显然为 \(j-v_i\),所以就说明了我们这个转移。
dp的一个要点就是关注当下。
时间复杂度 \(O(nm)\)。
有限背包/多重背包
每个物品有有限个。
多增加的量——每种物品有多少个。
如果采用无穷背包的思想,根本不知道物品选了多少个。
在考场上做出来一个基本没见过的东西基本不可能,要把考场上的问题变成见过的问题,每一个部分变成已经做过的题
原始方法是枚举选多少个。
考虑把 \(num_i\) 拆成 \(2^0+\ldots +2^j+k\)。
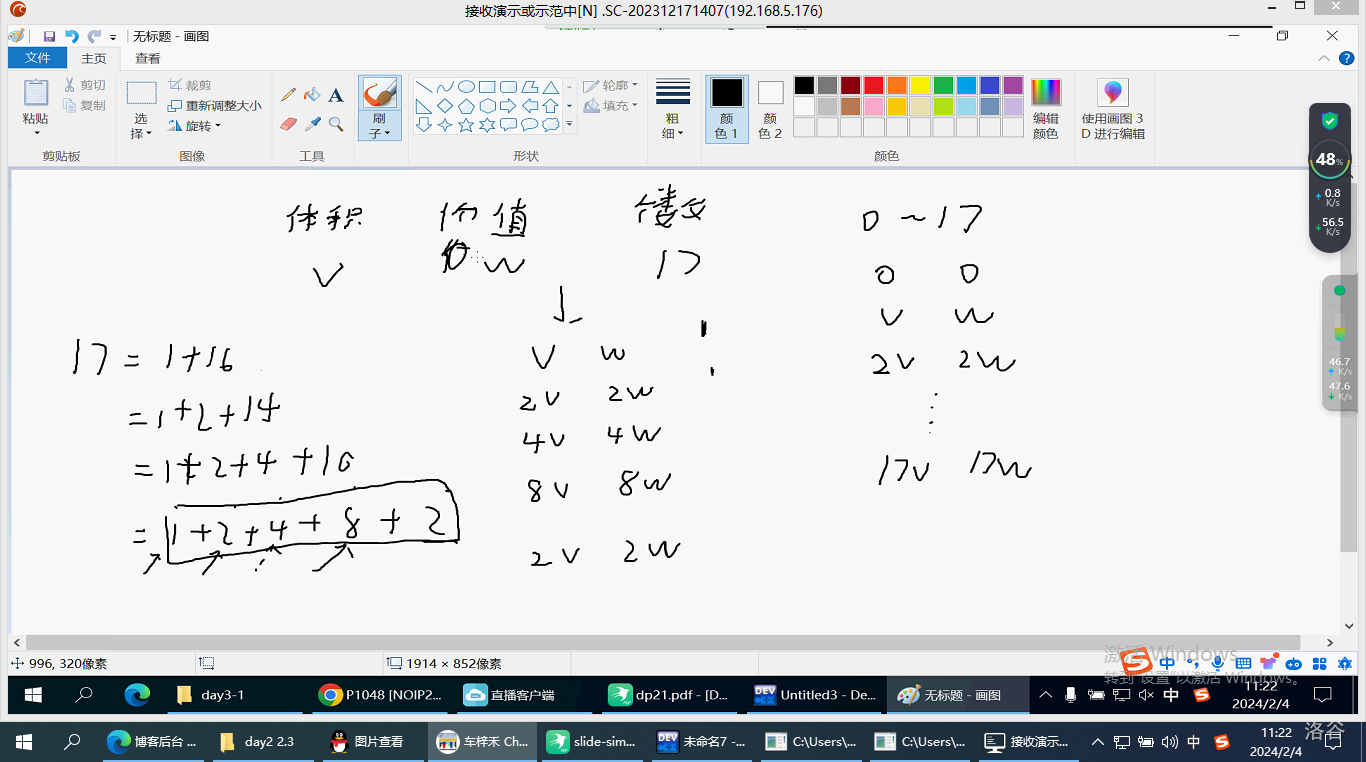
发现两种方法是等价的。
因为都可以枚举出所有选择的个数。
因为无论一个一个选还是按照新的方法选都可以组合出选 \(0\sim 17\) 个的情况。
如果仍不理解,可以从旧的dp与新的dp本质上是否有什么不同的方向进行考虑。
但是现在每个物品只有一个,一个物品会拆出来 \(\log n\) 个物品。
所以就变成了 \(n\log n\) 个物品。
直接 01 背包。
复杂度 \(O(nm\log n)\)。
//01背包问题
//每个物品只有选或者不选两种情况
f[i][j]:前i个物品用了j的体积所能获得的最大价值
for (int i=1;i<=n;i++)
for (int j=0;j<=m;j++)//要求f[i][j]
{
f[i][j] = f[i-1][j];//不选
if (j>=v[i]) f[i][j]=max(f[i][j], f[i-1][j-v[i]]+w[i]);//选
}
//无穷/完全背包问题
//每个物品有无数个
f[i][j]:前i个物品用了j的体积所能获得的最大价值
for (int i=1;i<=n;i++)
for (int j=0;j<=m;j++)//要求f[i][j]
{
f[i][j] = f[i-1][j];
if (j>=v[i]) f[i][j]=max(f[i][j], f[i][j-v[i]]+w[i]);
}
//有限/多重背包问题
//每个物品有有限个
//二进制拆分
cin >> cnt;//原始总共有cnt个物品
for (int i=1;i<=cnt;i++)
{
int tiji,jiazhi,geshu;
cin >> tiji >> jiazhi >> geshu;
int k=1;
while (k<=geshu)
{
n++;
v[n] = tiji*k;
w[n] = jiazhi*k;
geshu -= k;
k=k*2;
}
if (geshu != 0) {
n++;
v[n] = tiji * geshu;
w[n] = jiazhi * geshu;
}
}
//跑01背包
Eden 的新背包问题
考虑将一个物品去掉,可以看做前面和后面拼起来,于是正着一遍背包,倒着一遍背包,最后答案 \(\max_{0\le x\le V}(f_{i-1,x}+g_{i+1,V-x})\)。
问题:如果最优方案的前者体积和后者体积加起来小于 \(V\) 怎么办?
等待解答。
数位dp
给定 \(l,r\),求 \(l\sim r\) 有几个数。
数学的角度,显然有 \(r-l+1\) 个数。
\(f(l,r)=f(0,r)-f(0,l-1)\)
实际上要解决 \(f(0,x)\)。
即求有多少 \(0\le y\le x\)。
设 \(x\) 有 \(n\) 位。
假设允许前导0,\(y\) 也有 \(n\) 位。
转移方法:从高位开始一位一位去填 \(y\) 的值。
状态:\(f_{i,0/1}\) 代表从高到低填完第 \(i\) 位,0 代表填 \(y\) 之前的数位小于 \(x\),否则等于 \(x\),的方案数
一般情况下,\(0\sim 9\) 都可以填。
考虑什么时候不合法,就是前面都等于 \(x\) 的情况。
枚举该数位上能填的数 \(k\)。
转移:\(f_{i,(j==1)&&(k==up)}+=f_{i+1,j}\)。
为什么不能 \(f_{i,0}\) 从 \(f_{i+1,1}\) 转移过来?
等待解答。,ok。
初始化:\(f_{n+1,1}=1\)
数位dp和其它dp最不一样的一点:进行前缀和转换,需要注意清空。
一次复杂度大概为 \(O(n)\),其中 \(n\) 为位数,常数极大。
通用转移方法:枚举下一位填什么
给定 \(l,r\),求 \(\sum\limits_l^rf(i)\)。
其中,\(f(x)\) 代表 \(x\) 数位上所有数字之和。
令 \(w_{i,0/1}\) 代表已经填完 \(w\sim i\),此时价值。
转移:\(w_{i,(j==1)&(k==up)}+=f_{i+1,j}\times k+w_{i+1,j}\)。
\(f\) 用来计算方案数,\(w\) 用来记录数位之和,互相转移。
windy 数
dp做不了——加维度
增加维度 \(k\) 代表第 \(i\) 为 \(k\) 时的方案数。
转移时需要合法。
统计答案时需要枚举最低位填什么。
初始化解决前导0的方法:手动把最高位填好
后面听不懂。
Blinker 的仰慕者
黑
加维度——当前重要度为 \(j\)。
发现开不下。
发现 \(k\) 的质因数只能有 \(2,3,5,7\),考虑记录 \(2,3,5,7\) 出现的次数。
把一个维度拆成四个维度。
鉴于一点听不懂能力所限,建议看第一篇题解。
区间dp
合并石子
合并相邻是区间dp的关键词
状态:\(f_{l,r}\) 代表把第 \(l\sim r\) 堆石子合并为一堆的最小代价。
任意一个时刻合并出来的石子堆都对应原来的一段区间。
初始化:\(f_{l,l}=0\)
转移:\(f_{l,r}=\min\limits_{k=l}^{r-1}(f_{l,k}+f_{k+1,r}+sum_r-sum_{l-1})\)
\(sum_i\) 代表 \(\sum\limits_^ia_i\)。
注意合并要加上两堆石子的数量。
注意转移是从区间短的向区间长的转移。
区间dp需要从区间长度开始枚举
时间复杂度 \(O(n^3)\)。
环形石子合并
区间dp解决环形情况
会合并 \(n-1\) 次,但有 \(n\) 条边。
发现一定有一条边不用,就等价于这条边不需要,直接断开环。
将序列复制一遍后接在原序列后面,对这个序列做区间dp,发现对于每条边断开后的情况都能及时取出答案。
时间复杂度 \(O(n^3)\)。
- 能量项链
给定字符串,求回文子序列个数,1000 hdu4632
令 \(f_{l,r}\) 表示 \(l\sim r\) 中有多少个回文子序列。
状态设计显然。
发现一个比较显然的转移:\(f_{l,r}=f_{l+1,r}+f{l,r-1}-f{l+1,r-1}\)。
发现如果有新的回文子序列,开头结尾一定是 \(l\) 和 \(r\),所以如果 \(s_l=s_r\),\(f_{l,r}+=f_{l+1,r-1}\)。
为什么不+1?
等待解答。
状态:维护 \(l\sim r\) 的某些信息
转移:
- 枚举断点,关键:合并||相邻
- 扔掉最左边或者最右边,关键:子序列



