椭圆曲线加密笔记
数学知识
域:一组元素的集合,以及在集合上的四则运算,构成一个域。其中加法和乘法必须满足交换、结合和分配的规律。加法和乘法具有封闭性,即加法和乘法结果仍然是域中的元素。域中必须有加法单位元和乘法单位元,且每一个元素都有对应的加法逆元和乘法逆元。但不要求域中的 0有乘法逆元。单位元:单位元和其他元素结合时,并不会改变那些元素。 通常使用e来表示。逆元:若ab=ba=e,则称a为b的逆元,b为a的逆元。本原多项式:域中不可约多项式是不能够进行因子分解的多项式,本原多项式 (primitive polynomial)是一种特殊的不可约多项式。当一个域上的本原多项式确定了,这个域上的运算也就确定了。通过将域中的元素化为多项式形式,可以将域上的乘法运算转化为普通的多项式乘法再模本原多项式。
椭圆曲线定义
实数域上一组点集(x,y)满足
就是一条椭圆曲线。\(4a^3+27b^2 \neq0\) 是为了保证曲线不包含奇点。
奇点:尖点或自相交。
奇点示例:
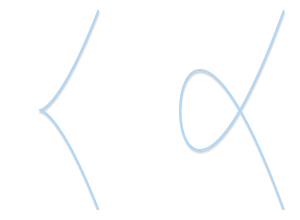
另外,无穷远点也是椭圆曲线的一部分,以0表示无穷远点。
运算
加法运算:取一条直线与椭圆曲线相交,这条直线和椭圆曲线相交的三点为P, Q, R(皆非零)。定义他们的总和等于0,\(P+Q+R=0\)。这里的0前述提到的单位元。
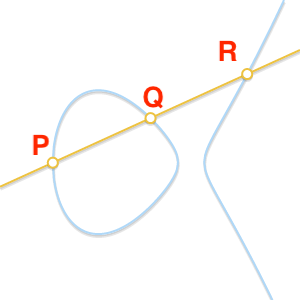
PQR同一直线上三点的顺序任意交换不影响加法运算总和,椭圆曲线上的点集属于阿贝尔群,也就是可交换群。
逆元
由\(P+Q+R=0\) 可以推知 \(-Q=P+R\)
那么-Q又是什么呢?-Q+Q=P+R+Q=0,容易想到,给定一个椭圆曲线上点Q,经Q画一条直线,这条直线与椭圆曲线仅交于两个点,一个点是Q,另一个自然就是-Q了。
这样的直线有两种情况,一种是直线经此点相切,另一种就是过此点作垂直于x轴的直线。
先讨论作垂线的情况,由$y^2 =x^3 +ax+b $可知,椭圆曲线关于x轴对称。那么另外一点,也就是-Q,自然就是Q关于x轴对称的另一点了。也就是这条直线与椭圆曲线相较于无穷远点0。
倍点运算
那么切线的情况呢?于切线我们可以通过渐进的方式,即P不断接近Q,直到P与Q重合,直线也就成了切线。
在这种情况下,可以写成\(Q+Q+R=0\),也就是\(R=(-Q)+(-Q)\)。
是的,虽然很难理解,但是在直线与椭圆曲线相切的情况下,另一点是-2Q。
这就是倍点运算。
既然有了 -2Q,很容易我们就能得到2Q,也就是-R。有了2Q与Q,把他们连起来,-3Q与3Q也是手到擒来。
以此类推,对于已知参数的椭圆曲线,给定点Q,得到它的n倍点,只需要按部就班计算即可。得益于计算机的算力,这并不复杂。
注意,n的取值应当使nQ不为无穷远点。
验证点
现在我们已知两个非零非对称的椭圆曲线点\(P(x_P,y_P)\)和\(Q(x_Q,y_Q)\),过此两点的直线交椭圆曲线于点\(R(x_R,y_R)\)。
非常容易验证点R是否与P,Q处于同一直线和椭圆曲线上,不再赘述。
有限域实践
以上阐述和图形都建立在坐标连续的情况下,实践中我们常用有限域(伽罗华域, Galois Field)上的椭圆曲线。有限域又可分为素数域\(GF(P)\)与二进制域\(GF(2^m)\)。
之所以要引入有限域,是因为有限域中的加法和乘法具有封闭性,即加法和乘法结果仍然是域中的元素,实践中我们不可能对变量取无穷多的值进行计算,
\(GF(P)\)上的椭圆曲线:
a,b,x,y均在有限域\(GF(p)\)中取值,即取值在\({0,1,2,3...,p-1}\)。p为大于3的素数。
p为素数时,才能保证集合中的所有的元素都有乘法逆元(0除外)。即对于域中的任一个元素a,总能在域中找到另外一个元素b,使得a*b mod p 等于1。
说明:假如p等于10,其乘法单位元为1。对于元素2,找不到一个数a,使得2*a mod 10 等于1,即2没有乘法逆元。这时,在域上就不能进行除2运算。
实例:在\(GF(23)\)上的椭圆曲线\(y^2\equiv x^3+x(mod 23)\)。
点\((1,5)\)在该椭圆曲线上,因为:
\(5^2=25\),
\(1+1=2\),
\(25(mod 23)=2\)。
二进制域\(GF(2^m)\)上的椭圆曲线:
\(a,b,x,y\)均在有限域\(GF(2^m)\)中取值
当 b = 1 时 , 方程表示的曲线称Koblitz曲线,是椭圆曲线密码体制实现中速度最快的曲线。
为了保证单位元性质,\(GF(2^w)\)上的加法运算和乘法运算,不再使用一般的加法和乘法,而是使用多项式运算。
在实践中,为了保证安全强度,有限域常常取得很大,当前来说\(GF(2^m)\)中m取160是合适的,即2的160次方这么大。
椭圆曲线公私钥
给定已知椭圆曲线上一点G和倍数k,计算k倍点 K,即
\(K=kG\)
知道G和k, 计算K是容易的,但是已知K和G,得到k却是困难的。所以我们可以将G和K 发送出去,k保留。K就是我们常说的公钥 , k则是私钥。
加解密
选定已知椭圆曲线E,其上一点G。生成私钥k,计算得到公钥K。
现在用户Alice可以将椭圆曲线E的参数和基点G, 公钥K发送给用户Bob。
Bob收到这些参数后,将需要加密的信息m编码到这个椭圆曲线上一点M,并产生随机数r。计算两个参数。
\(C1=M+rK=M+rkG=M+kC2\),
\(C2=rG\),
这里的M点是未经加密的信息,C1则是信息经过了公钥加密的点,C2点则是Bob的随机数r倍G点。
可以看到,Bob也生成了一个r倍点C2, 并利用r乘以Alice的公钥,本质上实现了Alice和Bob的两个随机数r和k一起对M点进行加法运算。
Alice收到C1和C2后,进行计算
\(C1-kC2=M+kC2-kC2=M\)
现在,Alice得到了信息m,这个过程中,即使攻击者获得了C1,C2,椭圆曲线E,基点G,也无法破解加密信息。
参考资料:
1.《应用密码学》胡向东等。
2. 伽罗华域(Galois Field)上的四则运算
3. 椭圆曲线加密算法原理解析(ECC)
4. 椭圆曲线加密原理与应用


 浙公网安备 33010602011771号
浙公网安备 33010602011771号