匹配与网络流学习笔记（在学习中）

\(upd:\)删去了某些读者认为很繁琐的笔者的思考过程

匹配与网络流学习笔记

基本概念

匹配

给定二分图\(G=(V,E)\)的一个子图\(G'=(V',E')\)，如果任取\(E'\)中的两条边\((u_1,v_1),(u_2,v_2)\)，有\(u_1,v_1,u_2,v_2\)两两互不相同，或者\(E'\)中仅有一条边，则称\(G'\)是\(G\)的一个匹配。

最大匹配

\(G'=(V',E')\)是原图的一个匹配，且不存在原图的另一个匹配\(G''=(V'',E'')\)，使得\(|E''|>|E'|\)，则\(G'\)是原图的一个最大匹配。

点覆盖

\(G=(V,E)\)，取其点集的一个子集\(V'\),如果对任意边\((u,v)\in E\)，有\(u\in V'\)或者\(v\in V'\)，则称\(V'\)是原图的一个点覆盖。

路径覆盖

有向图\(G=(V,E)\)，取若干条路径，使得图上每个点都至少在一条路径上，则称为原图的一个路径覆盖。单个点也是一条路径。

最大独立集

选择最多的点，满足两两之间没有边相连。

源点

有向图中入度为\(0\)的一个点，只出不进。

汇点

有向图中出度为\(0\)的一个点，只进不出。

交错路

始于非匹配点，且由匹配边和非匹配边交错而成。

增广路

在匹配问题中：始于非匹配点且终于非匹配点的交错路。显然，增广路上非匹配边比匹配边多\(1\)。

在网络流问题中：从源点\(s\)到汇点\(t\)的一条路，且这条路上每条边的容量\(-\)实际流量\(>0\)。

增广

在匹配问题中：把增广路上的非匹配边变成匹配边，匹配边换成非匹配边的过程。

增广路定理

当找不到增广路时，得到最大匹配。

最大匹配=最小点覆盖

显然最小点覆盖\(\geq\)最大匹配数，因为最小点覆盖需要把所有的边都覆盖了，而最大匹配并非需要用到所有边，所以可能需要更多的点。

下面考虑使得最小点覆盖\(=\)最大匹配数的策略。

对于一个在最大匹配中的边，它两侧的点至多有一个连接了未被匹配的点。否则，我们设这个边为\((u,v)\)，并且设\(u\)和\(v_1\)相连，\(v_1\)未被匹配，\(v\)和\(u_1\)相连，且\(u_1\)未被匹配，那么显然我们可以用\((u,v_1)\)和\((u_1,v)\)来代替\((u,v)\)，这样得到的匹配更优（比原来多\(1\)）。

现在，最大匹配中的边变成了两类，一类是连接了\(1\)个不在匹配中的点的边，一类是\(2\)个端点都在匹配中的点的边。对于第一类边，在取最小覆盖的时候，我们直接取这条边上的匹配点即可，在这部分中有几条边就得选几个点，然后我们把这些边删去。

现在就只需要考虑两端点都匹配的边了。显然，由于已经没有只有一个点匹配的边了，所以剩下的图里面的边要么是两个端点都匹配了，要么是都没匹配。经过分析可知，两个点都没匹配的边不可能存在，如果存在，我们就可以直接再把它匹配了，这样更优了，所以图里面所有的边应该都是两个端点都匹配了的，只不过是匹配的边和没匹配的边交替出现罢了。显然，有几条匹配边，我们还得选几个点去覆盖，这样我们便构造出来了一组覆盖使得最小点覆盖\(=\)最大匹配数。

综上，最小点覆盖\(=\)最大匹配数。

最大独立集=总结点数-最小点覆盖=总结点数-最大匹配数

由于最大匹配=最小点覆盖，所以最小点覆盖可以是一个独立集，最小点覆盖的补集也是一个独立集（考虑二分图的特点），并且，最小点覆盖中少任何一个点都会使得有边没被覆盖，这导致补集就不能是独立集了，所以最小点覆盖的补集就是最大独立集。

有向二分图中，最小路径覆盖=总结点数-最大匹配数？

没搞懂证明呢。

基本算法与实现

匈牙利算法

我们考虑把二分图分成左右两部分，每次枚举左边集合里的一个点\(u\)，然后枚举右边集合内的点\(v\)，如果\(v\)还没有被匹配，则可以完成匹配；否则，考虑之前与\(v\)匹配的那个点\(x\)，看看\(x\)还能不能和\(v\)之外的点\(y\)匹配，如果能的话，就让\(x\)与\(y\)匹配，\(u\)和\(v\)匹配，可以看出来这样的话就相当于把一条增广路上的匹配边和未匹配边取反了，和原来相比是多匹配了一条边。算法执行完之后，得到二分图的最大匹配。
代码实现请先看该题

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int M=1e5+9;
const int N=1e3+9;
ll n,m,e;
vector<ll> graph[N];
bool match[N],vis[N];
ll raw[N];
ll ans=0;
ll read();
bool dfs(ll now);
int main(){
//	freopen("in.txt","r",stdin);
	n=read();
	m=read();
	e=read();
	ll u,v;
	for(int i=1;i<=e;i++){
		u=read();
		v=read();
		graph[u].push_back(v);
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			vis[j]=false;
		}
		dfs(i); 
//		printf("i:%d\n",i);
	}
	printf("%lld\n",ans);
	return 0;
}
bool dfs(ll now){
	vector<ll>::iterator i;
	bool flag;
	for(i=graph[now].begin();i!=graph[now].end();i++){
		ll tmp=*i;
		if(vis[tmp]) continue; //防止匹配到原配 
		vis[tmp]=true;
		if(!match[tmp]){ //如果tmp没匹配 
			match[tmp]=true;
			ans++; 
			raw[tmp]=now; //记录原配 
			return true; //匹配成功 
		} else { //如果tmp匹配过了 
			flag=dfs(raw[tmp]); //看一下原配还能不能和别的匹配 
			if(flag){ //如果可以，就找到了增广路 
				match[tmp]=true;
				raw[tmp]=now;
				return true;
			} 
			//否则失配 
		}
	}
	return false;
}
inline ll read(){
	ll ret=0,f=1;
	char ch=getchar();
	while(ch<'0' || ch>'9'){
		if(ch=='-'){
			f=-1;
		}
		ch=getchar();
	}
	while(ch>='0' && ch<='9'){
		ret=10*ret+ch-'0';
		ch=getchar();
	}
	return ret*f;
}

一般图匹配的带花树算法

可能这辈子都不一定学会了

EK（Edmond-Karp）算法

该算法用于解决最大流问题，即从\(s\)注水，问最多有多少水能到\(t\)。

考虑能从\(s\)到\(t\)的所有路径，对于每一条路径来说，它能流到\(t\)的流量，最大不会超过这条路径上的最小边权。

以此为基本目标，我们不断在网络中找增广路，每找到一条增广路，就把这条路上所有的边的边权减去该路径上最小的边权\(minweight\)，意味着这些"管道"都已经被占用了\(minweight\)的流量了，在找其他路时就不能按照原边权去流了。当找不到增广路时，流量就"应该"最大了。

但是很容易想到，这种方法与搜索的顺序有关系，很有可能有一个本能流过很大流量的管道被其他很多小流占用，而这些小流本可以走其他的流量小的管道，这导致真的大流来的时候反而流不动了（这个问题和在做背包问题时用贪心策略出的问题是一个道理），请参考下面前两张图来感性理解这种情况，看过之后请回来看解决方案。

那么这个问题怎么解决呢？在背包问题中，最暴力的暴搜做法虽然效率低，但保证了正确性，原因是它可以回溯，回溯之后相当于把物品从背包中又拿了出来，以消除当时决策的影响。在这里我们可不可以用类似的方法来做呢？感觉这样需要\(dfs\)套\(bfs\)，实现起来很麻烦，效率的话，由于所有的情况都被枚举了，所以效率也不太好。

那么怎么做能效率更高地解决正确性问题呢？我们再回顾一下出现问题的原因：小流量不小心流到了大流量的管道里面，使得大流量管道在之后没法让大流量通过那么多了。我们当然不可能主动地让小流量往小管道里跑，但是我们可以这样做：假如我的小流量真的不小心流到你的大流量管道里面了，我可以做一个标记：虽然我占用了您的大流量管道，但是现在我的小流量管道是空着的，您但用无妨。

\(EK\)算法就是用一个很巧妙的方式来实现这个标记的：在图中加反向边。初始时对于每条原图中的边，我们都加一条容量为\(0\)的反向边。当找到一条增广路时，除了让每条路径上的边减去\(minweight\)之外，我们让这条路上所有的反向边加上\(minweight\)。

比如，原网络是这样的：

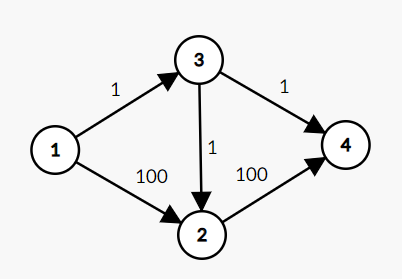
我们找到了\(1->3->2->4\)这条路，并且让流量流过去了，则图变成了这样：

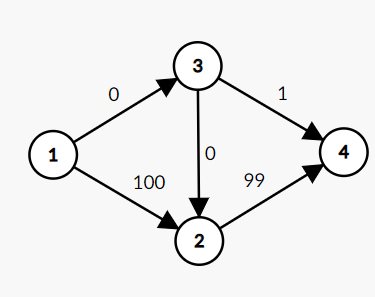
显然，原本能最大流\(101\)的网络，现在只能流\(99+1=100\)了，因为上面的小流走错路了，为了修正，我们考虑按照\(EK\)算法过程加反向边之后的结果（\(upd:\)手画反向边修复了边权重叠的问题）：

这样的话，再找增广路时，我们可以找到\(1->2->4\)以及\(1->2->3->4\)，其中后者就是上面所说的"虽然我占用了您的大流量管道，可因此现在我的小流量管道是空着的，您但用无妨"。显然，如果没有反向边，第二条路在原图中是不可能走的，所以一系列反向边就是给后来流过的流的标记。

反向边最开始就应该全部加上。如果用链式前向星存图，假如当前边的编号是\(now\)，则\(now\ xor\ 1\) 就是反向边的编号了，原理不难理解：我们一次加两条相反的边，假如边下标从\(0\)开始存，一个为奇数边，一个为偶数边，异或正好就是这两个互相转化。

总结一下，\(EK\)算法的过程就是这样了：不断寻找从\(s\)到\(t\)的增广路（这里就是最小边权\(>0\)的路径），找到之后就把路径上的正向边的边权都减去\(minweight\)，反向边边权都加上\(minweight\)，\(ans+=minweight\)，最后直到找不到增广路，那么\(ans\)就是最大流了。

下面考虑代码实现。我先是经历了一番自己的思考和实现，写出了个大概，通过了一定数量的测试点，练了练代码能力，但是因为实现太差而爆空间和时间，故不再展开说自己的尝试了，我们直接看别人的优秀的设计与实现。

一种实现是这样的，存储路径时这样设计结构体：

struct Pre{
    ll v; //当前点的前一个点
    ll edgenum; //v与当前点的边的编号
};

实现代码时，大佬的思路是先\(bfs\)一次，找到最短的一条增广路（如果能的话），增广路的信息存储在了一个公用的数组中，然后我们往前扫一遍走过的边，找到最小值，然后再重新扫一遍走过的边，加减相应的权值。

\(EK\)算法的复杂度是\(O(nm^2)\)的，并不能通过本题，但是作为几乎最简单的最大流算法，还是要学会的。

代码如下：

#include <bits/stdc++.h>
#define ll long long
#define INF 999999999999
using namespace std;
const int N=205;
const int M=1e4+9;
typedef struct{
	ll v;
	ll edgenum;
}NB;
typedef struct{
	ll from,to,nxt,weight;
}Edge;
Edge edge[M];
ll head[N],cnt,n,m,s,t,ans;
NB pre[M];
bool inqueue[N];
int bfs();
void EK();
void add(ll x,ll y,ll w);
int main(){
	ll x,y,w;
	scanf("%lld %lld %lld %lld",&n,&m,&s,&t);
	for(int i=1;i<=n;i++){
		head[i]=-1;
	}
	for(int i=1;i<=m;i++){
		scanf("%lld %lld %lld",&x,&y,&w);
		add(x,y,w);
		add(y,x,0);
	}
	EK();
	return 0;
}
void EK(){
	while(bfs()){
		ll minweight=INF;
		for(ll i=t;pre[i].v>0;i=pre[i].v){ //找到最小边权 
			minweight=min(minweight,edge[pre[i].edgenum].weight);
		}
		for(ll i=t;pre[i].v>0;i=pre[i].v){ //依次加上或者减去 
			edge[pre[i].edgenum].weight-=minweight;
			edge[pre[i].edgenum^1].weight+=minweight;
		}
		ans+=minweight;
	}
	printf("%lld\n",ans);
}
int bfs(){
	queue<ll> q;
	ll now;
	for(int i=0;i<M;i++){
		pre[i].edgenum=0;
		pre[i].v=0;
	}
	for(int i=0;i<N;i++){
		inqueue[i]=false;
	}
	q.push(s);
	inqueue[s]=true;
	while(!q.empty()){
		now=q.front();
		q.pop();
		for(ll i=head[now];i>=0;i=edge[i].nxt){
			if(!inqueue[edge[i].to] && edge[i].weight>0){ //之前没加入到队列中，且是增广路 
				pre[edge[i].to].edgenum=i; //记录这条边的编号 
				pre[edge[i].to].v=now; //记录上一个点
				inqueue[edge[i].to]=true; //入队 
				q.push(edge[i].to); 
			}
		}
		if(now==t){//如果当前点是终点，那么说明找到了增广路 
			return 1;
		}
	}
	return 0;
} 
inline void add(ll x,ll y,ll w){
	edge[cnt].from=x;
	edge[cnt].to=y;
	edge[cnt].nxt=head[x];
	edge[cnt].weight=w;
	head[x]=cnt++;
}

Dinic算法

前面所讲的\(EK\)算法，除了加反向边以外，可以说思路还是比较自然的。但是，\(EK\)算法并不高效。为什么呢？假设网络中有很多条增广路，然而我们做一次\(bfs\)，只是找到最短的一条，然后把边权修改完之后还要重新\(bfs\)，这样是一种浪费。如果我们能在一次完整的\(bfs\)之后，找到很多条网络中的增广路就好了，这样我们就通过减少\(bfs\)的次数而提高了效率。

\(Dinic\)算法的基本想法就是上面我们所说的那样。我们考虑到\(EK\)中一次\(bfs\)求出来一条网络里的最短增广路就草草return了，但我们不满足呀，要是它能找到当前网络中所有的最短增广路就好了。基于此，我们用\(bfs\)对图进行分层，即标记\(s\)到每个点的最短步数，把步数相同的点看成同层点。如果每次我们都从某一层往下一层跳，并最终能跳到\(t\)的话，那它显然就是一条最短增广路。并且，我们容易发现满足这样的跳跃条件的路一般都不只一条，所以通过分层\(bfs\)就相当于找到了所有的从\(s\)到\(t\)的最短增广路。

别高兴得太早，虽然我们一次\(bfs\)就找到了好几条最短增广路，但是我们还得想想怎么快速修改这些增广路的边权。以前在\(EK\)算法中，我们可以通过记录每个点的上一个经过点来记录路径，现在有好多路，都存下来太费空间了，得想个办法。这时候，我们想到刚才说的每次往下一层跳，如果这样能跳到\(t\)，就一定是最短增广路，所以我们根本没必要记录路径，只需要进行一次\(dfs\)，每次到一个点的时候，我们就让它强制往比它深一层的点去跳，\(dfs\)过程中记录最小边权，走到头就回溯回去减掉最小边。

考虑到\(dfs\)的性质，我们可以想到这么一个实现方案：对于一个点\(u\)来说，它可能在多条增广路上，也就是说它可能有多个前驱和后继。考虑一下之前怎么求一个子树的大小，我们是每算完一棵子树的大小，然后加到父亲结点上，最终算出树的大小。在这里我们可以用类似的思想，先统计这个点到底要减去多少流量，统计完之后在回溯时一步到位直接减掉。这样的话，一次\(dfs\)就修改了多条增广路，真正实现了加速。用代码描述就是这样：

while(bfs()){
    ans+=dfs();
}

按照这个思路写出代码，提交一次之后会惊奇地发现，\(TLE\ on\ case\ 9\) ，虽然这个已经比\(EK\)优秀了，但是似乎还可以继续优化的样子。

没错，还可以继续优化的。

先讲第一个优化：剪枝。我们考虑\(dfs\)中的这句话：

ll k=dfs(edge[i].to,min(edge[i].weight,sumflow));

如果\(k=0\)，那么意味着后面的全都消耗完了，所以\(edge[i].to\)这个点以及之后的点在本次\(dfs\)中再次被走到时就不能再走了，所以我们可以令\(depth[edge[i].to]=-1\)，破坏层次关系，一行代码就能加速。洛谷模板题加上该优化之后即可\(AC\)。

下面就是喜闻乐见的代码实现了(不加优化和优化一只差一行，在\(dfs\)函数里面，仅多了一行剪枝)：

#include <bits/stdc++.h>
#define ll long long 
#define INF 999999999999999
using namespace std;
const int N=205;
const int M=1e4+9;
typedef struct{
	ll from,to,nxt,weight;
}Edge;
typedef struct{
	ll head[N],cnt,n,m,s,t,depth[N],maxflow; //定义图相关数据
	Edge edge[M];
	bool inqueue[N];
    
    //定义操作图的方法
	
	inline void init(){ //图的初始化 
		n=read();
		m=read();
		s=read();
		t=read();
		for(int i=0;i<=n;i++){
			head[i]=-1;
			inqueue[i]=false;
		}
		cnt=0;
		maxflow=0;
	}
	
	inline void fresh(){ //每次bfs前都要调用一次，消除掉上一次bfs的结果 
		for(int i=0;i<=n;i++){
			inqueue[i]=false;
			depth[i]=-1; 
		}
	}
	
	inline void add(){ //加边，同时加0反向边
		ll x,y,w;
		x=read();
		y=read();
		w=read();
		edge[cnt].from=x;
		edge[cnt].to=y;
		edge[cnt].weight=w;
		edge[cnt].nxt=head[x];
		head[x]=cnt++;
		edge[cnt].from=y;
		edge[cnt].to=x;
		edge[cnt].weight=0;
		edge[cnt].nxt=head[y];
		head[y]=cnt++;
	}
	
	inline bool bfs(){ //对残量网络进行bfs，找到最短的增广路，并且对图进行分层 
		queue<ll> q;
		ll now;
		fresh(); //把上一轮bfs的pre和depth消除了 
		q.push(s);
		depth[s]=0;
		inqueue[s]=true;
		while(!q.empty()){
			now=q.front();
			q.pop();
			for(ll i=head[now];i>=0;i=edge[i].nxt){
				if(!inqueue[edge[i].to] && edge[i].weight>0){ //找没访问过的且有剩余流量的边 
					inqueue[edge[i].to]=true; //入队标记防止重复访问 
					depth[edge[i].to]=depth[now]+1; //分层 
					q.push(edge[i].to);
				}
			}
		}
		if(depth[t]==-1) { //对整个图bfs完了之后再看能否到t 
			return false;
		}
		return true;
	}
	
	
	ll dfs(ll now,ll sumflow){
		//sumflow可以认为是流入这个点的流量 
		ll useflow=0; //统计流出的流量 
		if(now==t){
			return sumflow;
		}
		for(ll i=head[now];i>=0 && sumflow>0;i=edge[i].nxt){ //注意流量不能变成负的
			if(depth[edge[i].to]==depth[now]+1 && edge[i].weight>0){ //既不能超过边的容量，也不能超过剩下的没流走的流量
				ll k=dfs(edge[i].to,min(edge[i].weight,sumflow));
				if(k==0) depth[edge[i].to]=-1; //重要的剪枝 
				edge[i].weight-=k;
				edge[i^1].weight+=k;
				useflow+=k;
				sumflow-=k;
			}
		}
		
		return useflow;
	} 
	
	void dinic(){ //图的最大流算法
		while(bfs()){
			maxflow+=dfs(s,INF);
		}
	}
	
	inline ll read(){ //快读，可以不要
		ll ret=0,f=1;
		char ch=getchar();
		while(ch<'0' || ch>'9'){
			if(ch=='-'){
				f=-1;
			}
			ch=getchar();
		}
		while(ch>='0' && ch<='9'){
			ret=10*ret+ch-'0';
			ch=getchar();
		}
		return ret*f;
	}
}Graph;
Graph graph;
int main(){
//	#define DEBUG
	
	#ifdef DEBUG
		freopen("in.txt","r",stdin);
	#endif
	graph.init();
	for(int i=0;i<graph.m;i++){
		graph.add();
	}
	graph.dinic();
	printf("%lld\n",graph.maxflow);
	return 0;
}

第二个优化叫做当前弧优化。\(dfs\)中，先被遍历到的边肯定是已经增广过了，并且已经确定无法继续增广了，这条边以后必然不会走。那么下次我们再到达该节点时，就可以在循环起始就设置不遍历这些边。在实现上，我们就记\(cur[i]\)为\(i\)结点当前已经走过的最后一条边的编号，其作用类似于链式前向星中的\(head[i]\)，然后，我们每次\(dfs\)就从\(cur[now]\)而不是\(head[now]\)开始走就好了。

代码如下，请注意比较和上一份代码的不同，您可以把两份代码拷贝到这里迅速看出他们的不同：

#include <bits/stdc++.h>
#define ll long long 
#define INF 999999999999999
using namespace std;
const int N=205;
const int M=1e4+9;
typedef struct{
	ll from,to,nxt,weight;
}Edge;
typedef struct{
	ll head[N],cnt,n,m,s,t,depth[N],maxflow; //定义图相关数据
	Edge edge[M];
	bool inqueue[N];
	ll cur[N]; 
    
    //定义操作图的方法
	
	inline void init(){ //图的初始化 
		n=read();
		m=read();
		s=read();
		t=read();
		for(int i=0;i<=n;i++){
			head[i]=-1;
			cur[i]=-1;
			inqueue[i]=false;
		}
		cnt=0;
		maxflow=0;
	}
	
	inline void fresh(){ //每次bfs前都要调用一次，消除掉上一次bfs的结果 
		for(int i=0;i<=n;i++){
			inqueue[i]=false;
			depth[i]=-1; 
		}
	}
	
	inline void add(){ //加边，同时加0反向边
		ll x,y,w;
		x=read();
		y=read();
		w=read();
		edge[cnt].from=x;
		edge[cnt].to=y;
		edge[cnt].weight=w;
		edge[cnt].nxt=head[x];
		head[x]=cnt++;
		edge[cnt].from=y;
		edge[cnt].to=x;
		edge[cnt].weight=0;
		edge[cnt].nxt=head[y];
		head[y]=cnt++;
	}
	
	inline bool bfs(){ //对残量网络进行bfs，找到最短的增广路，并且对图进行分层 
		queue<ll> q;
		ll now;
		fresh(); //把上一轮bfs的pre和depth消除了 
		q.push(s);
		depth[s]=0;
		inqueue[s]=true;
		cur[s]=head[s];
		while(!q.empty()){
			now=q.front();
			q.pop();
			for(ll i=head[now];i>=0;i=edge[i].nxt){
				if(!inqueue[edge[i].to] && edge[i].weight>0){ //找没访问过的且有剩余流量的边 
					inqueue[edge[i].to]=true; //入队标记防止重复访问 
					depth[edge[i].to]=depth[now]+1; //分层 
					cur[edge[i].to]=head[edge[i].to];
					q.push(edge[i].to);
				}
			}
		}
		if(depth[t]==-1) { //对整个图bfs完了之后再看能否到t 
			return false;
		}
		return true;
	}
	
	
	ll dfs(ll now,ll sumflow){
		//sumflow可以认为是流入这个点的流量 
		ll useflow=0; //统计流出的流量 
		if(now==t){
			return sumflow;
		}
		for(ll i=cur[now];i>=0 && sumflow>0;i=edge[i].nxt){
			cur[now]=i;
			if(depth[edge[i].to]==depth[now]+1 && edge[i].weight>0){ //既不能超过边的容量，也不能超过剩下的没流走的流量
				ll k=dfs(edge[i].to,min(edge[i].weight,sumflow));
				if(k==0) depth[edge[i].to]=-1; //重要的剪枝 
				edge[i].weight-=k;
				edge[i^1].weight+=k;
				useflow+=k;
				sumflow-=k;
			}
		}
		
		return useflow;
	} 
	
	void dinic(){ //图的最大流算法
		while(bfs()){
			maxflow+=dfs(s,INF);
		}
	}
	
	inline ll read(){ //快读，可以不要
		ll ret=0,f=1;
		char ch=getchar();
		while(ch<'0' || ch>'9'){
			if(ch=='-'){
				f=-1;
			}
			ch=getchar();
		}
		while(ch>='0' && ch<='9'){
			ret=10*ret+ch-'0';
			ch=getchar();
		}
		return ret*f;
	}
}Graph;
Graph graph;
int main(){
//	#define DEBUG
	
	#ifdef DEBUG
		freopen("in.txt","r",stdin);
	#endif
	graph.init();
	for(int i=0;i<graph.m;i++){
		graph.add();
	}
	graph.dinic();
	printf("%lld\n",graph.maxflow);
	return 0;
}

最小费用最大流算法

这个问题就是，我们的网络中的管道不仅有流量这一属性，还有单位流量流经的花费的属性（比如您可以理解为买票坐车，每个人走的时候都要买票，不同路的票价同）。我们想在保证最大流的情况下，消耗最小费用（注意不要把问题描述错了）。

显然，不管它每条路花费怎么样，我们都得先保证最大流，所以肯定还是要找增广路不断增广，直到没法增广为止。只不过，在求增广路的时候，我们想让费用最小。对于一条增广路来说，其从\(s\)到\(t\)经过的管道中的流量都是一样的，都是最小的那个流量值，所以在流量一定的情况下，为了让花费最少，我们只需要让这条路从\(s\)到\(t\)的流量的单位花费之和最小就好了。为了让单位花费之和最小，相当于求最短路，另外别忘了我们现在是在找增广路，所以我们要用最短路算法来代替\(bfs\)的过程。在这里我使用了\(spfa\)算法，因为在加边的时候，我们的反向边会设置\(cost_{reverse}=-cost\) ，原因可以理解为反向走要退钱。在这里我使用了\(EK\)最大流算法，这足以\(AC\)（\(2020/7/18\)）洛谷最小费用最大流模板题，当然，您也可以用\(dinic\)做。