决策树与集成

Decision Tree

目录

• Decision Tree
  • Classification Tree
  • Regression Tree
  • Regularization
  • Pros and cons
  • Assemble Method
    • Bagging
    • Boosting
  • Takeaway

Greedy, Top-down, Recurrent

Classification Tree

misclassification loss is not suitable for decision tree loss, because

\[L(R_p) - (\lambda L(R_1)+(1-\lambda) L(R_2)) \]

can not always be guaranteed > 0.

we usually use Cross-Entropy Loss.

\[L_{misclass}(R)=1-\max(\hat{p},1-\hat{p}) \\ L_{cross}(R)=L_{cross}(\hat{p})=-\hat{p}\log \hat{p} - (1-\hat{p})\log (1-\hat {p}) \]

the \(L_{misclass}\) is not strictly concave uniformly.

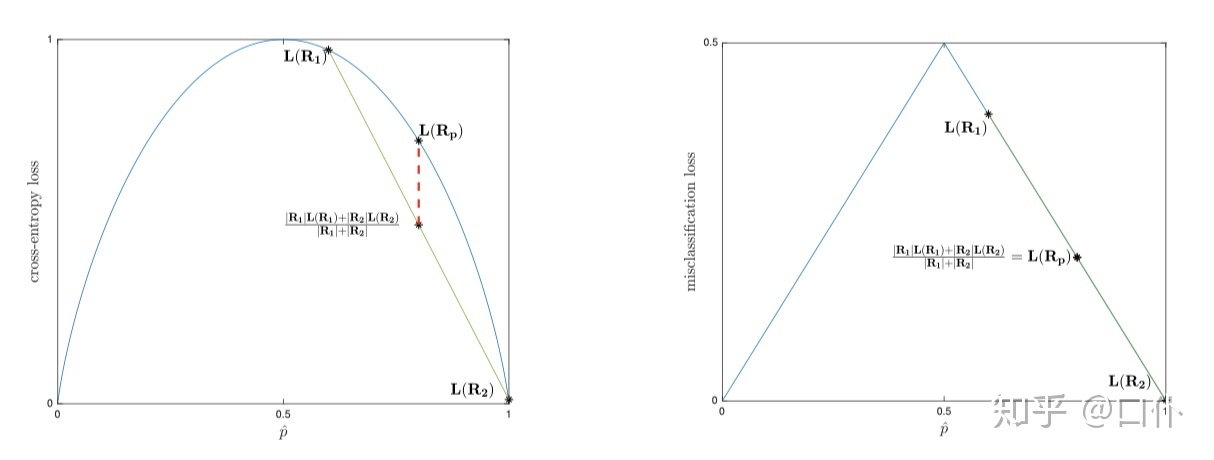
( from https://zhuanlan.zhihu.com/p/146964344 )

\[p_{parent}=\frac {R_1 \hat{p_1}+R_2 \hat{p_2}}{R_1+R_2} \]

Regression Tree

Output the average value of region R.

We use Square Loss

\[L = \frac{\sum(y_i-\hat{y})}{|R|} \]

Regularization

• 「最小化叶子规模」：当区域的基数低于某个阈值时，停止分割该区域
• 「最小化深度」：如果某个区域进行的分割次数超过了某个阈值，则停止分割
• 「最小化节点数量」：当一个树拥有了超过某个阈值的叶子节点，则停止生长

Prune after building the tree.

( from https://zhuanlan.zhihu.com/p/146964344 )

Pros and cons

cons: High variance, not support additive model very well

Assemble Method

\[Var(\bar{X})=\rho \sigma^2+\frac{1-\rho}{n}\sigma^2 \]

so if we want to reduce the Var, we can increase the number of models or cut down \(\rho\)

Bagging

bagging is Bootstrap Aggregation. Decrease Var

• bootstrap

  P is total population, S is the training set

  suppose that S=P, sample Z from S to guide a sub model.

  bootstrap samples \(Z_1,Z_2,...,Z_M\) train \(G_m\) on \(Z_m\)

  reduce \(\frac{1-\rho}{M}\) bias is larger

• aggregation

  \[G(x)=\frac{\sum_{m=1}^M G_m(x)}{M} \]

• Random Forest

  at each split, consider only a fraction of your total features

  decrease the correlation(\(\rho\)) between models

Boosting

Decrease Bias

the assemble is additive(not average).

the misclassified cased will be weighted more in the next tree's training process.

Adaboost:

\[G(x)=\sum_{m} \alpha_m G_m \]

\(\alpha_m\) for \(G_m\) is \(\log (\frac{1-err_m}{err_m})\)

Takeaway

( from https://zhuanlan.zhihu.com/p/146964344 )