强化学习
Reinforcement Learning
目录
Background
Credit Assignment Problem: Explore how actions in an action sequence contribute to the outcome finally.
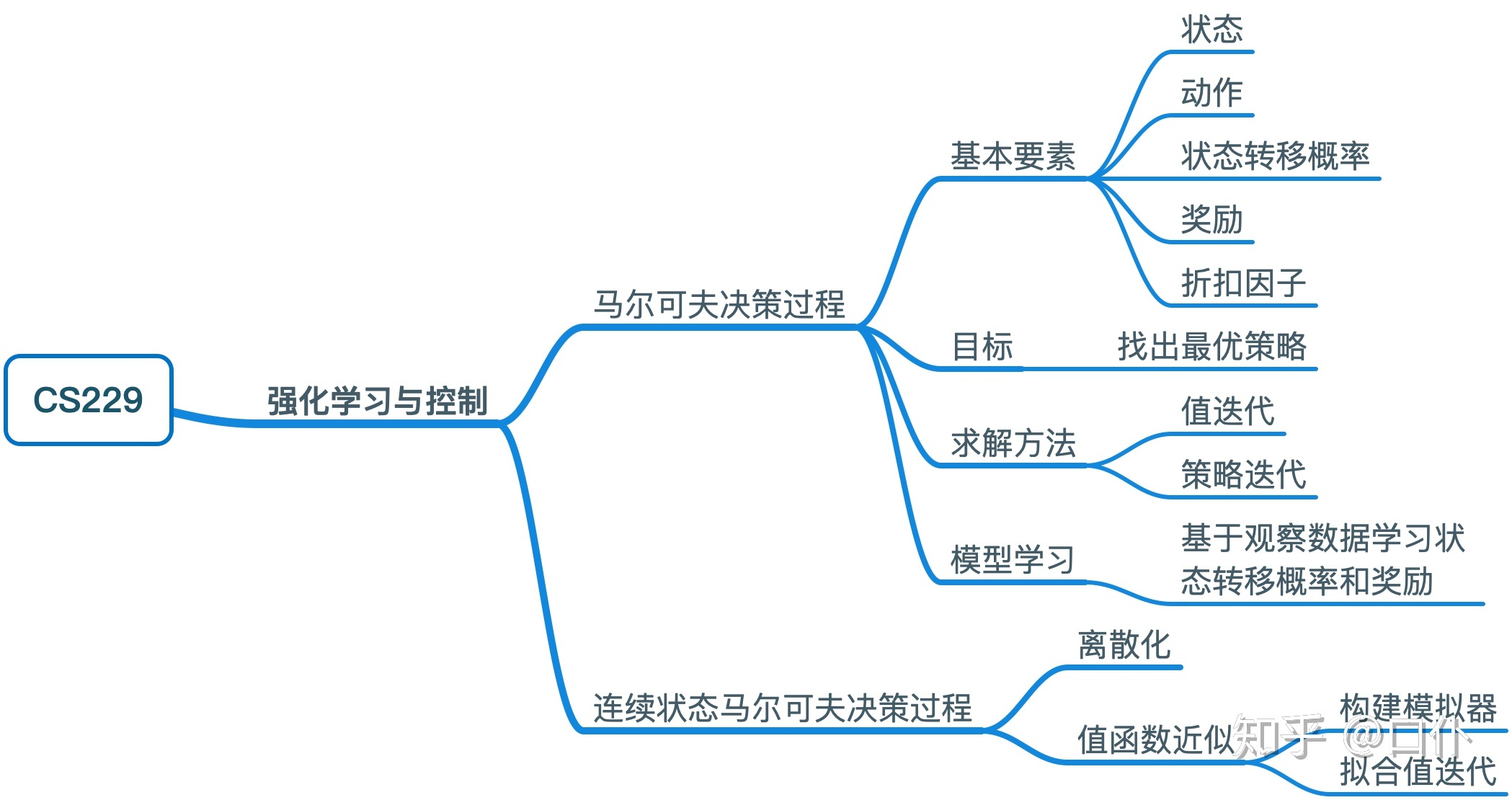
MDP(Markov Decision Process)
Formulation: \((S,A,\{P_{sa}\},\gamma,R)\)
Goal: choose actions over time so as to maximize the expected value of the total payoff.
Bellman Equation
\[V^\pi(s)=R(s)+\gamma\sum_{s'\in S}P_{s,\pi(s)}(s')V^\pi(s')
\]
Value and Policy Iteration
Skip.
Learning a model for MDP
We are not given state transition probabilities and rewards explicitly.
Finite-horizon MDPs
Formulation: \((S,A,\{P_{sa}^{(t)}\},\gamma,R^{(t)})\), the \(T>0\) is time horizons, the payoff id defined as
\[R(s_0,a_0)+...+R(s_T,a_T)
\]
in finite cases, \(\gamma\) is not necessary anymore.
the policy \(\pi\) sometimes is non-stationary in finite-horizon setting.
can be solved by dynamic programming
LQR
Linear Quadratic Regulation
linear transitions:
\[s_{t+1}=A_t s_t+B_t a_t+w_t
\\\text{where}\,\,
w_t \sim \mathcal{N}(0,\Sigma_t)
\]
quadratic rewards
\[R^{(t)}(s_t,a_t)=-s_t^T U_t s_t - a_t^T W_ta_t
\]
U and W are positive definite matrices.