面向对象第一单元总结——表达式求导
前言
经过轻松愉悦紧张刺激的学习，终于完成了OO第一单元的全部程序设计部分，相比于不温不火的pre，第一单元作业令我倍感折磨。第一单元中完成了理解需求、设计架构、代码书写、测试构造、程序调试的一整套的软件开发的流程，并且参加了一次探讨课，和同学们分享了我的第一次作业设计思路，高效的表达在真实的软件协作开发中非常重要。通过第一单元作业，我完整体验了一把软件开发的微缩版。
本门课程为面向对象设计与构造，我在完成作业的过程中也是有一定刻意地使自己按照对象的思维来思考，并多多使用继承和多态，来实现类与类之间的作用关系，完成之后回顾第一次作业，有很多地方还有待提高，所以通过本文总结优缺点，并思考改进方向。
复杂度度量预备知识
第一次使用代码复杂度度量工具MetricsReload，在此梳理一下几个复杂度数值的含义：
方法复杂度[1]
ev(G)基本复杂度衡量程序非结构化程度，基本复杂度高意味着非结构化程度高，难以模块化和维护。
iv(G)模块设计复杂度衡量模块判定结构，即模块和其他模块的调用关系；模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。
v(G)圈复杂度衡量一个模块判定结构的复杂程度，根据程序从开始到结束的线性独立路径数量计算得到，圈复杂度越高，代码越复杂越难维护。
类复杂度[2]
OCavg 类方法的平均循环复杂度
WMC 类方法权重，可粗略理解为方法数量等
程序设计思路与度量分析
第一次作业
总体思路
第一次作业表达式的形式比较简单，求导规则非常单一，没有嵌套等涉及递归的计算规则。我是用正则表达式对表达式进行提取，只需要按照指导书的表达式的形式化定义依次写出正则表达式即可。之后对每一项匹配得到系数和幂指数，执行求导操作，之后进行同类项的合并，这里我使用TreeMap<exponent,coefficient>结构来进行化简，最后就是关于0、1、-1、x**2等化简技巧的事情了。
以下是我的正则匹配过程（第二、三次作业基本沿用了这一过程）：使用find()、group()对表达式依次匹配项，对项依次匹配因子，之后按照不同种类的因子进行解析。
类图分析
U1A1Main：主函数入口，负责表达式字符串的传入，调用解析和求导方法，并输出求导结果。
Polynomial：多项式类，这个类内置TreeMap<exponent,coefficient>来存储每一项的幂次与系数，根据功能多项式类需要表达式字符串完成解析，并调用单项式类解析单项式，用于构建多项式，并完成求导、化简和输出。
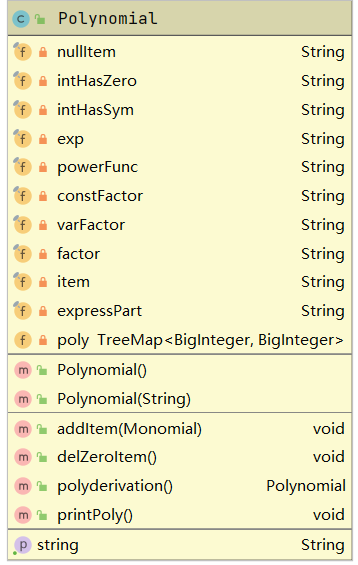
Monomial：单项式类，利用多项式类中切割得到的项字符串解析，得到幂指数和系数，返回给多项式类，单项式类中也需要实现求导和输出操作。
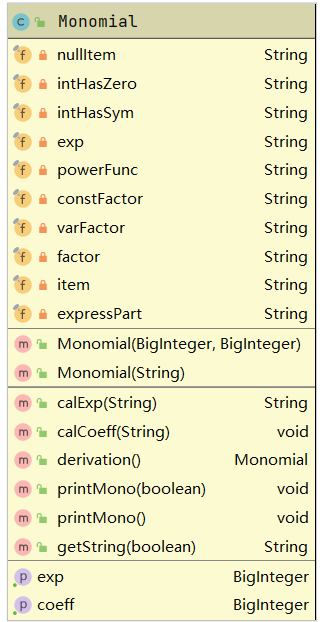
优缺点分析
优点：
①本次作业比较简单，分成了两个类实现起来比较简洁，而且类之间通过解析和求导联系起来，耦合度比较低。
②正则表达式按照形式化定义有层次地写出，结构清晰便于调试。
缺点：
①有些功能的实现不够分离，解析的部分分别粘附在Polynomial、Monomial类中，优化分散在不同的层次，toString()、delZeroItem中均有优化相关代码，不易调试。
②每个类方法数量过多，抽象层次不够深，没有抽象到因子层面，只能在单项式层面处理幂函数，在后期支持三角函数和表达式嵌套时无法扩展。
③final类型的字符串重复存储，浪费空间，增加了维护的工作量，更说明字符串解析功能应当单独成模块。
度量分析
第一次作业度量分析中每个方法的三种复杂度都控制在10以下，方法复杂度不高，但是Monomial类复杂度过高。
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| Monomial | 3.20 | 7 | 32 |
- 总体分析
分析本次作业，我的Monomial和Polynomial类都将字符串解析过程放在其中作为对象的创建方法，更好的策略应当把字符串解析单独作为一个类，然后只需要把解析好的多项式和单项式传递给相应的类。本次作业中出现了许多冗余的方法，大量的化简分散在两个类中，toString方法较为复杂，寻找正的项的过程放入了toString方法中，显然这个可以通过重写TreeMap排序方法解决这个问题，或者将这个寻找正项的过程单独形成一个方法。
Monimial类：
属性个数：12
方法个数：10
方法规模：从代码行数看，方法规模较大的为getString calExp calCoeff方法，这些方法与单项式信息提取、字符串处理相关，这也是bug出现较多的方法。
方法控制分支数目：从圈复杂度看，toString等字符串构造方法分支较多，与递归输出的结构相关。
类总代码规模：133行，属于一个比较合理的范围。
Polymial类：
属性个数：11
方法个数：7
方法规模：从代码行数看，toString等字符串构造方法规模较大，主要是各种特殊情况的化简使得这些方法较为复杂。
方法控制分支数目：所有的方法圈复杂度均较低，分支数目不算太多。
类总代码规模：87行，属于一个比较合理的范围。
- 内聚耦合情况：字符串解析与化简均耦合在
Monomial和Polynomial类中，且分布比较分散。其中Monimial类的WMC指标比较高，循环依赖性较高，与其调用关系复杂关系密切。
第二次作业
总体思路
第二次作业引入了三角函数并支持了表达式因子，我第一次的结构只对于幂函数有效，考虑到第一次的代码量也不是很多，也为了更好地拓展第三次作业，于是我重写了一份代码。
第二次作业中我仍然沿用了正则表达式，为了支持表达式因子的识别，我采取了如下策略：对表达式扫描确定最外层括号，并用&、%对其进行标记，最坏情况会带来\(O(n^2)\)的算法复杂度。
本次作业的求导环节要求支持嵌套求导，于是我采用了二叉表达式树来进行求导，为此我对于每一种运算建立了“运算门”：Const Var Power Sin Cos Multiply Add，在每一种运算门中定义了节点的创建方法和求导方法，解析表达式的过程即完成二叉树的建构，求导时只需要执行根节点的求导便可得到导函数的二叉树。
相比于第一次作业，本次作业化简显得非常重要，化简可以使长度取得显著的缩短。受制于二叉树的结构，我只在节点的创建中进行了部分优化，力图减少节点的数量，如当创建操作数为x与1的Multiply节点返回x的Var节点，在Add、Power节点的创建中也进行了类似的优化。对于幂的合并与同类项的合并，我借鉴了“三元组”的策略，从二叉树的叶子结点自底向上进行创建，使用HashMap<Triple,Coefficient>进行化简，通过Add、Multiply进行乘法与加法的合并化简，从而在自动地拆开了表达式中所有的括号，最终得到每一项都是\(a*x**b*sin(x)**c*cos(x)**d\)的标准形式的表达式，本次优化做的非常彻底，性能分基本上都能拿到99+的分数。
类图分析
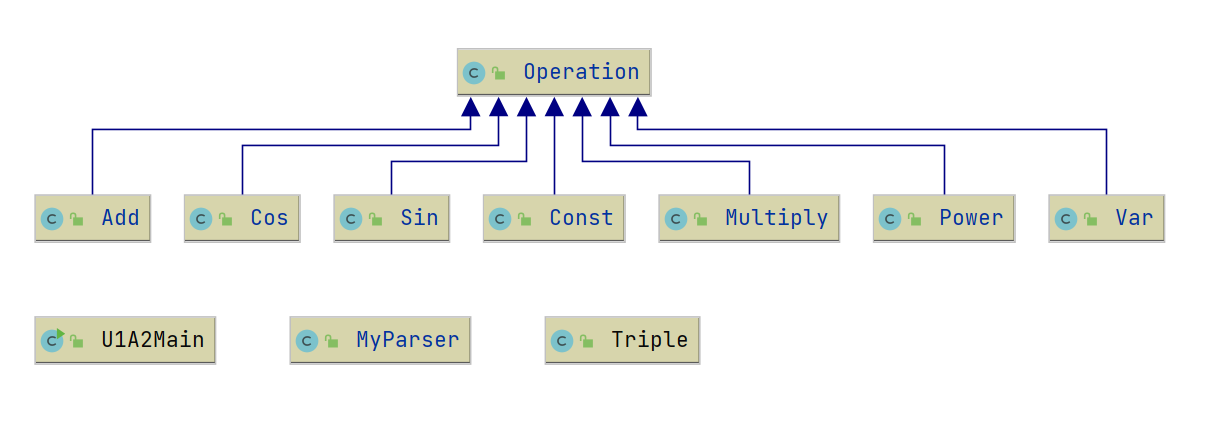
总体来看类与类之间层次关系非常清晰。
U1A2Main：主函数入口。
MyParser：传递字符串，使用层次化定义的正则表达式对表达式进行表达式、项、因子的解析，并得到一棵二叉树。
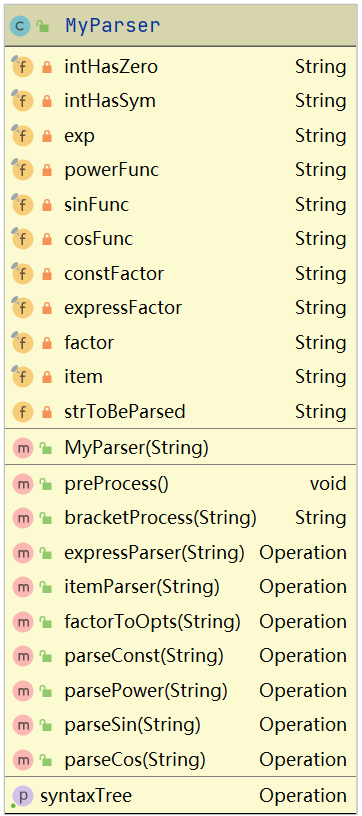
如输入\(sin(x)*(x+5)+x**-8\)，可以返回如下一棵二叉树的根节点。
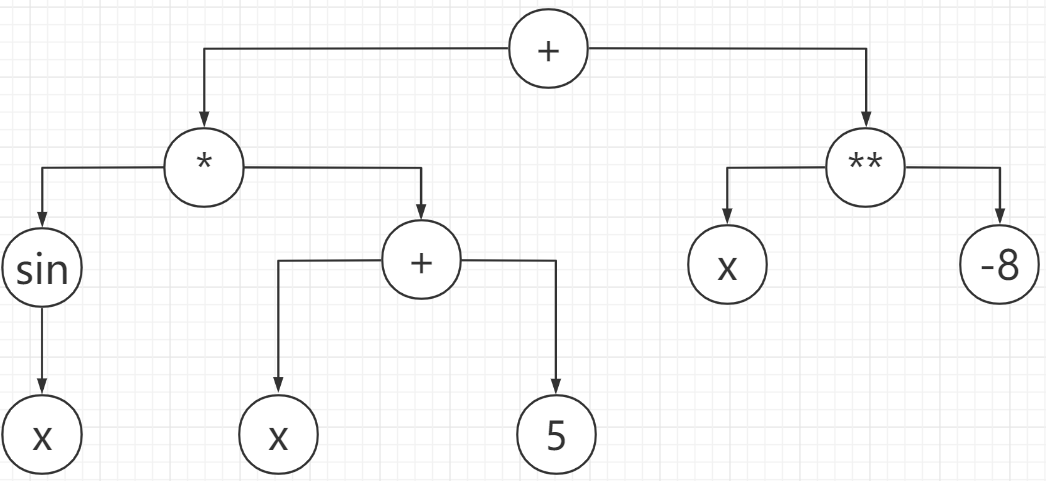
Triple：三元组类型，存储幂函数、三角函数的幂指数，将合并操作转换为三元组的加、乘运算。
Operation：抽象运算符类，实现了求导等方法，将各种运算符统一起来。
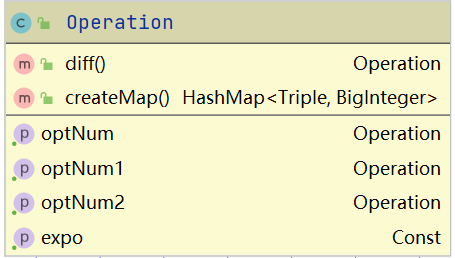
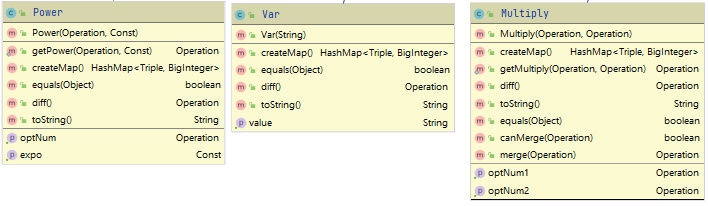
Const Var Power Sin Cos Multiply Add：具体的运算符类，实现了创建和求导方法，有的实现了getXXX静态方法，用于建树过程中的化简，可以实现希望创建类型与实际返回类型的不一致，如使用getPower()创建操作数为x与1的Multiply节点返回x的Var节点。
优缺点分析
优点：
①抽象深度深，将每一种运算抽象出来，建立了二叉树结构，其创建、维护与求导操作均较多叉树优越。
缺点：
①二叉树结构化简较为困难，所以另外组织了基于HashMap存储的三元组结构，但是三元组结构对嵌套的支持能力较弱，仅能支持普通表达式的嵌套处理，在三角函数嵌套面前无能为力。
②HashMap的处理方法耦合在每一个运算门类，耦合度较高。
度量分析
第二次作业许多大量方法的ev(G)复杂度过高，主类U1A2Main、Triple的复杂度过高。
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Add.getAdd(Operation,Operation) | 6.0 | 4.0 | 4.0 | 7.0 |
| Multiply.equals(Object) | 6.0 | 5.0 | 3.0 | 7.0 |
| Multiply.getMultiply(Operation,Operation) | 10.0 | 8.0 | 6.0 | 9.0 |
| Triple.createTriple(Operation) | 11.0 | 9.0 | 5.0 | 9.0 |
| Triple.equals(Object) | 4.0 | 4.0 | 3.0 | 6.0 |
| Triple.toString() | 13.0 | 1.0 | 8.0 | 11.0 |
| U1A2Main.makeItem(String,HashMap) | 19.0 | 3.0 | 5.0 | 8.0 |
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| U1A2Main | 4.33 | 8 | 13 |
| Triple | 3.33 | 11 | 30 |
- 总体分析
makeItem、toString、createTriple、getMultiply方法复杂度显著地高，U1A2Main、Triple类复杂度较高，由于在主函数中用比较冗长的makeItem方法进行字符串的化简导致主函数比较复杂，应当将化简进一步内聚为单独模块；由于二叉树相较于多叉树的递归深度较深，递归调用时某些方法会被重复调用，所以导致toString、createTriple、getMultiply方法调用次数较多，要将部分方法从运算门类、Triple类中抽离开来，另外建立一个二叉树类，将递归操作集成到其中。
对复杂度较高的类进行进一步细致分析：
U1A2Main类：
属性个数：0
方法个数：3
方法规模：makeItem mapToString 方法行数在20行以上，功能为实现将存放三元组的hashMap转化为字符串，主类处理输入输出只应该停留在调用层面，细节性方法应该单独形成功能类。
方法控制分支数目：分支数目均较为合理。
类总代码规模：76行
Triple类：
属性个数：3
方法个数：9
方法规模：toString createTriple方法函数超过了20行，toString方法与化简输出有关，createTriple方法内部进行了大量的类型判断语句用于创建合适的节点类型，应当将这一部分集成到工厂，createTriple只负责调用即可。
方法控制分支数目：toString方法v(G)达到11，原因是要处理x、sin(x)、cos(x)各自的化简。
类总代码规模：121行
Multiply类：
属性个数：2
方法个数：8
方法规模：getMultiply较长，原因是getMultiply处理所有创建乘法节点时的简化规则。
方法控制分支数目：本类中各方法控制分支数目均在合理范围。
类总代码规模：99行
- 内聚耦合情况：本次作业中，没有出现
iv(G)数值过高的方法，说明模块之间的调用关系比较简单，耦合度较低。在Triple、Add、Triple中有许多方法的ev(G)数值较高，说明模块化不够好，许多功能并不能做到更好地抽象，内聚还有待提高。
第三次作业
总体思路
第三次作业相较于第二次作业难点是引入了格式检查与三角函数的嵌套，实现三角函数的嵌套对于我的二叉表达树结构来说非常容易，我只做了简单的修改变实现了这一功能。本次作业的难点是格式检查和引入三角函数嵌套的化简。
习惯了正则表达式简单清晰的优点，我不忍放弃这一简单的做法，所以我单独建立了一个SyntaxCheck类，学习了递归下降法进行格式检查，并没有把格式检查与表达式的解析一同完成，虽然会花费两倍的时间，但是实现了两个功能的解耦，毕竟格式检查是一个非常容易出错的环节。另外使用单独的SyntaxCheck类还可以方便地对自己的输出再进行格式检查，方便两个部分互相检查。
我的递归下降通过scanner实现对特定符号的识别，通过回滚机制实现对不同部分的解析，只需要把文法翻译一遍就可以实现功能，完全不需要考虑+++x、+++1等问题，正确的文法就可以识别出这些。我的方法需要很多数组索引的操作，非常繁杂要十分注意，我为了确定其中的一个回滚的bug花费了我两个小时的时间，这是一个缺点，但是这样实现就是逐个翻译文法，如果文法变化可以轻松地修改代码。
三元组的存储方法不再适用于含有三角函数嵌套的情形，并且在本次作业中，由于三角函数形式的多样化，拆开括号大概率不是良策，于是我仍然使用类似HashMap的结构，建立了叶子容器、乘法容器、加法容器来存储表达式并实现幂次与同类项的合并，本次作业我希望实现有某种特征的表达式因子括号的拆开，例如两个“多项式”相乘时把括号拆开并合并，同时对1、-1，0等进行优化，但是在最终提交前的两个小时中我测试出了化简的bug，于是权衡之下优先确保正确性，去掉了优化。最终某一些测试点性能分爆0了，虽然感到非常遗憾，但是考虑到我得到了全部的正确性，这也是当前情形下的贪心最优解了。
类图分析
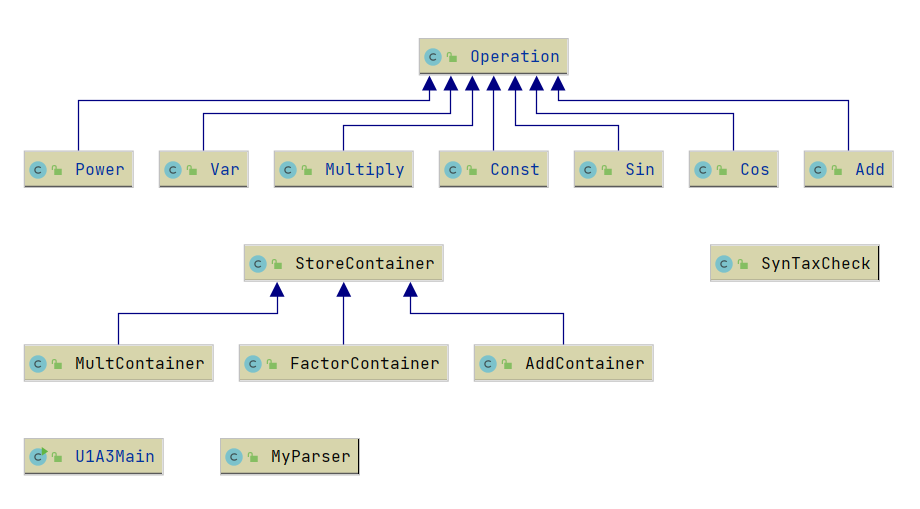
可以看出，第三次作业最大变化时新添加了StoreContainer和SynTaxCheck类。
U1A3Main：主函数入口。
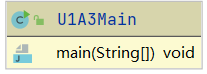
SynTaxCheck：语法检查类。将待检查字符串加上一层括号后，表达式具有统一形式用于处理。p1作为全局指针，用于扫描待检查字符串，scanner方法从p1所指字符串位置出扫描关键字符[0-9] + * ** x sin cos ( )，通过scanner的扫描结果，实现不同匹配方法的切换检查。
MyParser：解析类。除了创建节点时支持了三角函数的嵌套，其余与第二次作业相同。
Operation：运算门类。
Const Var Power Sin Cos Multiply Add：具体的运算门，支持了Sin Cos节点的嵌套功能，其余同第二次作业。
StoreContainer：存储容器类。作为抽象对象方便通过HashMap统一管理各个容器类，定义了创建与合并方法。因为需要使用HashMap结构，所以要为每一种子类重写equals()与hashCode()方法。
FactorContainer：基础节点容器类。使用tag属性标记节点容器类型，tag可以为“basic”，“sin”，“cos”，container容器用于存储嵌套内容，对于“basic”容器container为空。
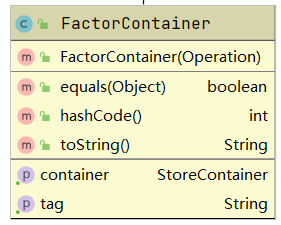
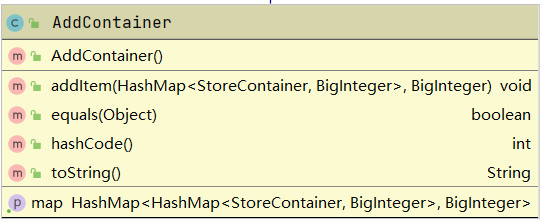
MultContainer：乘法容器类。使用HashMap存储项的常数部分与其余部分，并添加了因子的添加规则以实现幂指数的合并。
AddContainer：加法容器类。类似于乘法容器类，使用了hashMap存储项的系数与其余部分，其余部分也是用HashMap存储。添加了项的添加规则以实现同类项的合并。
优缺点分析
优点：
①最大程度利用了第二次作业已有的功能，做到了”在原有基础上扩展而不修改“的原则。
②存储层次独立为一个大类，摆脱了存储与节点的耦合，结构更加清晰。
缺点：
①语法检查与表达式解析分离，导致语法正确的情况下时间性能下降，语法检查过程中产生的信息没有被及时地利用。
②大量的HashMap嵌套使得存储量非常庞大，时间性能较差。
③没有使用工厂模式，在节点、存储容器的创建与合并中使用了大量的类型判断语句，代码不够精炼，判断逻辑复杂。
度量分析
第三次作业语法检查和化简的相关方法复杂度过高，存储类StoreContainer复杂度显著高；大量方法的ev(G)过高说明模块化做的依旧不够好，难以维护。
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Add.getAdd(Operation,Operation) | 6.0 | 4.0 | 4.0 | 7.0 |
| AddContainer.equals(Object) | 3.0 | 4.0 | 1.0 | 4.0 |
| AddContainer.toString() | 25.0 | 1.0 | 8.0 | 9.0 |
| FactorContainer.equals(Object) | 9.0 | 6.0 | 3.0 | 6.0 |
| FactorContainer.toString() | 3.0 | 4.0 | 3.0 | 4.0 |
| MultContainer.equals(Object) | 4.0 | 4.0 | 2.0 | 5.0 |
| MultContainer.toString() | 20 | 3.0 | 7.0 | 8.0 |
| Multiply.equals(Object) | 6.0 | 5.0 | 3.0 | 7.0 |
| Multiply.getMultiply(Operation,Operation) | 10.0 | 8.0 | 6.0 | 9.0 |
| Power.getPower(Operation,Const) | 12.0 | 7.0 | 4.0 | 7.0 |
| StoreContainer.createContainer(Operation) | 7.0 | 8.0 | 8.0 | 8.0 |
| StoreContainer.mergeAdd(StoreContainer,StoreContainer,AddContainer) | 20.0 | 4.0 | 8.0 | 8.0 |
| StoreContainer.mergeMult(StoreContainer,StoreContainer,MultContainer) | 20.0 | 4.0 | 8.0 | 8.0 |
| SynTaxCheck.isDigit(String) | 4.0 | 3.0 | 10.0 | 11.0 |
| SynTaxCheck.scanner() | 11.0 | 6.0 | 5.0 | 16.0 |
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| StoreContainer | 6.25 | 8 | 25 |
| SynTaxCheck | 4.36 | 14 | 48 |
| MyParser | 2.62 | 7 | 34 |
- 总体分析
SyntaxCheck类中逐个字符读取并回滚的机制使得scanner、IsDigit等方法v(G)过高，存储层次依托HashMap进行嵌套的存储使得存储深度非常深，插入并合并同类项时equals进行大量的操作使得时间复杂度较高。
对复杂度较高的类作进一步分析：
MyParser类：
属性个数：12
方法个数：13
方法规模：factorToOpts和bracketProcess方法代码行数均超过了30行，factorToOpts中大量代码用于因子种类判断的分支，bracketProcess方法建了一个栈扫描字符串对最外层括号进行处理，分支语句占据了较多代码。
方法控制分支数目：该类中所有方法的控制分支数目均处于较低水平。
类总代码规模：187行
StoreContainer类：
属性个数：0
方法个数：4
方法规模：mergeAdd mergeMult createContainer代码规模均到达40行以上，比较复杂。createContainer方法中大量的分支控制代码，有大量创建类有关代码，这些应当集成到工厂中比较好。mergeAdd mergeMult分支中有大量冗余和强制类型转换。
方法控制分支数目：这个类中分支控制地还算合理。
类总代码规模：145行
- 内聚耦合分析：在本次作业中，
SynTaxCheck类中isDigit(String)方法耦合度较高，其余的各个类中方法的耦合度较低。StoreContainer类中大量方法的ev(G)数值较高，说明存储类中模块化做的不够好，一个功能的实现需要手动调用多个方法，增加了编程的困难度。
BUG分析
第一次作业
在解析幂函数的指数时使用了字符串替换，导致要替换的串如果是别的串的前缀时，会直接替换破坏别的串。可见字符串处理中应尽量使用非破坏性操作。由下图可以看到Monomial方法数量过多，并未进行很好地整合，使得难以精准调试定位这个bug，循环次数也比较多。
- 复杂度分析
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| Monomial | 3.2 | 7.0 | 32.0 |
从引发bug的方法看，在Momomial类中calExp操作中出现了bug,该方法代码行数为19，从ev(G) iv(G) v(G)可以看到该方法的分支数目较少，与其他模块调用与被调用关系简单，结构化合理，该方法执行单一功能，较为独立。但是内部由于对类内部的公有属性进行了修改并修改不慎考虑情况不周全，所以导致了bug的出现。由于复杂度不高，所以很容易被忽视，所以在之后的作业中，对于情况比较复杂的方法，还是应以方法为单位进行测试。
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Monomial.calExp(String) | 4.0 | 1.0 | 3.0 | 3.0 |
第二次作业
第二次作业强测与互测均未出现bug
第三次作业
第三次作业强测与互测均未出现bug。但是第三次作业的语法检查部分使用了大量的数组索引操作，花费了大量时间用于调试，可以参考同学的建议局部使用正则表达式减轻工作量。由下图可见大量的判断与回滚使得如下方法圈复杂度较高，恰恰也是回滚的数组索引操作比较繁琐。
- 复杂度分析
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| SynTaxCheck.isDigit(String) | 4.0 | 3.0 | 10.0 | 11.0 |
| SynTaxCheck.scanner() | 11.0 | 6.0 | 5.0 | 16.0 |
测试环节
第一次作业
使用python的Xeger库根据我的正则表达式自动生成样例，使用sympy库进行符号运算比较求导结果。Xeger自动生成过程完全随机，难以做到高覆盖，也无法调整每次测试的侧重点，为了避免自己的正则表达式出错，还需要使用参考同学的正则表达式进行交叉验证。
第一次互测环节基本上使用自己的测评机进行轰炸，并没有仔细地阅读room中的代码。
第二次作业
按照表达式的层次表达式、项、因子分别设计了python数据生成器，并且针对特殊数字设计了数据池，可以控制生成项的数目，嵌套的深度，各类因子的构成比例等，有效的实现了样例的覆盖。
第二次作业开始读他人的代码，对代码中逻辑混乱的部分设计测试用例进行攻击。如看到一名同学为了切割表达式字符串进行了反复的符号替换，并且前后之间有大量的关联，于是我使用所有的符号进行测试，发现其在-+-情况下的bug。
第三次作业
第三次作业我根据不同的测试点设计了一份样例清单，列举了格式错误类型、表达式化简结果为0等诸多我认为可能易出错的地方，并且进行了一定程度的组合，并在互测环节成功hack了一人。通过阅读代码，发现他在多层嵌套的表达式处理时出现了合并错误的bug。
重构经历总结
从上述三次作业的类图中可以清晰地看到程序结构的变化。
第一次作业完全没有预测需求的意识，仅仅考虑其为一个幂函数处理，所以抽象层次不够深刻，仅仅分为了Polynomial和Monomial类，并没有形成表达式、项、因子的递归式处理方法。
第二次作业有了一定预测意识，提前考虑了嵌套的处理，第二次作业相较于第一次可以说是重写而不是重构，建立了二叉树的表达式存储，使用三元组来辅助化简。
第三次作业保留了二叉树，放弃三元组结构重构了存储形式，使用支持嵌套的HashMap来进行层次化的存储，由于基于正则的方法在格式检查上难以奏效，于是构造递归下降的格式检查单元。
提升方向
学习使用设计模式，在更高层面上做到归一化处理。本次作业中调用方法的层面上出现了大量的类型判断语句，根据对象类型判断结果调用不同的方法，下一次可以考虑工厂模式，将对类型的判断集成到工厂类，并且尽量简化接口，尽量传递原始数据，将数据的任何处理集成到单独的数据处理模块。
模块还需要进一步解耦，每一个独立的模块可以写调试输出代码，进一步做到模块化调试。模块的功能比较单一，建立模块单元的测试树对单个模块进行独立测试，可以减轻构造整体测试树的复杂程度。
本次作业中随着我对代码的不断修改产生了大量冗余，已经学习了强大的git工具为什么不使用呢？通过git做好版本管理，此时可以大胆地删去其中冗余的代码，让自己的作业看起来赏心悦目。
心得体会
最大的感觉是最初一定要想好架构再写代码，必要时在纸上画一画帮助自己理清思路，也可以和同学们交流探讨，借鉴他人的优秀架构，也可以针对各种架构未来可能要应对的情况做一个预测，进而不断调整自己的架构，整个过程会多花费一些时间，但是这是一个加速型的回报，在第三次作业中体现的尤为明显。
完成作业后复盘才能够让自己的面向对象的思想得到提升，否则是纸上谈兵。第一单元可以说是试错的过程，终于知道了哪些行为是不好的行为。虽然感觉第一次的架构写起来还算比较舒服，但是有些不好的类让我每次使用的时候都要写很多辅助代码并且要十分注意接口，而且没有使用工厂模式，用了大量的switch、instanceof等让代码十分冗长，以至于这些思维含量不高的代码占据了大量篇幅，反而让精髓代码不够突出。
对JAVA语言使用地更加熟练了，至少作为一门编程语言可以说是大致掌握了。
参考文献
[1] https://blog.csdn.net/Dkangel/article/details/106279052
[2] https://blog.csdn.net/weixin_30635053/article/details/96879703
