2021.8.19 模拟赛 T4 题解

题目传送门

首先让我们一起痛骂数据！它给了个超过数据范围的数据！

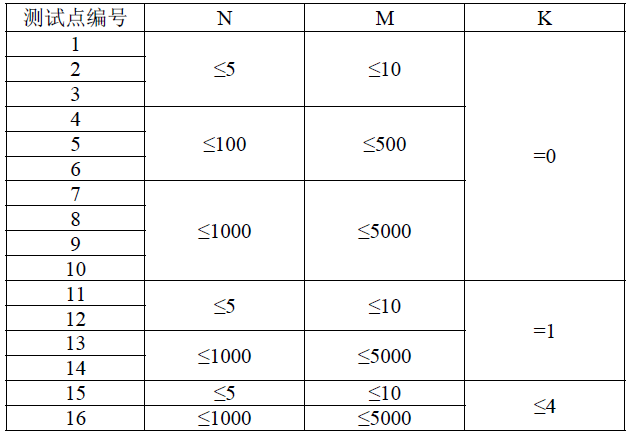
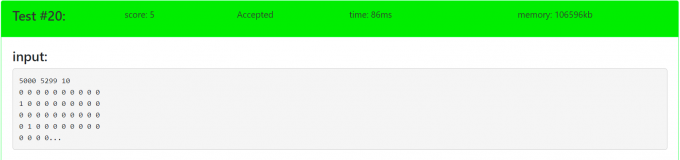
由于我习惯于建图时开二倍空间（即使是有向图），所以我侥幸过了……

实际上这道题的思路非常的简单。

用分层的思想，将钥匙视为状态，\(k<10\)，因此考虑将状态进行二进制的压缩。每条边的权值都为 \(1\)，因此可以直接用 BFS 进行转移，复杂度为 \(O(n\times2^k)\)，就可以了

#include<algorithm>
#include<bitset>
#include<cctype>
#include<cerrno>
#include<clocale>
#include<cmath>
#include<complex>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<limits>
#include<list>
#include<map>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<utility>
#include<vector>
#include<cwchar>
#include<cwctype>
#include<chrono>
#include<random>
#include<unordered_map>
using namespace std;

//#define int long long
#define ll long long
#define ull unsigned long long
#define rll register long long
#define ri register int
#define il inline

const int INF=0x3f3f3f3f,N=5e3+10;
int n,m,k,ans=INF;
int key[N],dis[N],f[N][N];
bool vis[N][N];
int cnt,head[N];
struct Edge{
    int to,nxt,val;
}e[N<<1];
struct node{
    int id,v;
};
queue<node> q;

il ll read(){
    ll x=0,y=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')
            y=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=x*10+c-'0';
        c=getchar();
    }
    return x*y;
}

il void add(int u,int v,int w){
    e[++cnt]={v,head[u],w};
    head[u]=cnt;
}

signed main(){
    n=read(),m=read(),k=read();
    for(ri i=1;i<=n;i++){
        for(ri j=1;j<=k;j++){
            key[i]<<=1;
            int h=read();
            key[i]+=h;
        }
    }
    for(ri i=1;i<=m;i++){
        int x=read(),y=read(),z=0;
        for(ri j=1;j<=k;j++){
            z<<=1;
            int h=read();
            z+=h;
        }
        add(x,y,z);
    }
    memset(f,63,sizeof(f));
    f[key[1]][1]=0;
    q.push((node){1,key[1]});
	vis[key[1]][1]=1;
    while(q.size()){
        node now=q.front();
        q.pop();
        vis[now.v][now.id]=0;
        for(ri i=head[now.id];i;i=e[i].nxt){
            int v=e[i].to,mid=now.v|key[v];
            if((e[i].val&now.v)==e[i].val&&f[mid][v]>f[now.v][now.id]+1){
                f[mid][v]=f[now.v][now.id]+1;
                if(!vis[mid][v]){
                    vis[mid][v]^=1;
                    q.push((node){v,mid});
                }
            }
        }
    }
    for(ri i=0;i<(1<<k);i++)
        ans=min(ans,f[i][n]);
    if(ans==INF)
        printf("No Solution");
    else
        printf("%d",ans);
    return 0;
}