匈牙利算法小讲

又名：匈牙利算法的封建

$ (bushi$

匈牙利增广路算法，简称匈牙利算法

原理：反转一条交错路径之后匹配边数\(+1\)，找增广路

我们先来假设一个通篇都要用到的前提：

现在有 \(n\) 名男生， \(m\) 名女生。其中有 \(k\) 对男女互有好感，保证不出现gay或百合

一人不一定只有一个人与之配对（即一个女生可以与多个男生互有好感，反之亦然）。

若一对互有好感，那么我们作为中介可以让两人原地结婚。但是不可重婚，那是犯罪

好了，请问我们最多能撮合出最多几对夫妻呢？

那么显然，我们应用二分图的知识解决问题，方法如下图：

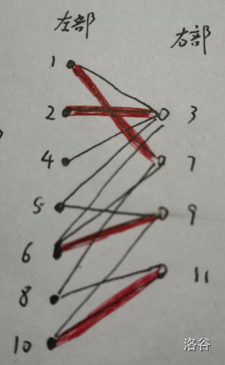
显然，假定男生们为主动方，如果他能找到的女生中有暂时没结婚的，就跟她结婚

但是我们会遇到一个问题：你得到的是否是最多对？

下图就是一个例子：

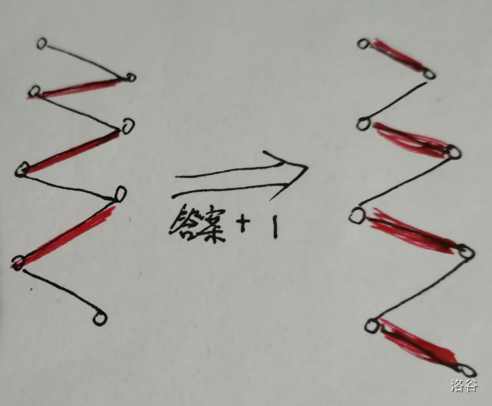
这时，我们所讲的匈牙利算法就派上用场了！

让我们以此图为例：

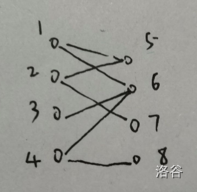
我们首先让 \(1\) 、 \(5\) 结婚，再给\(2\)介绍对象。

但我们经过查询发现： \(2\) 有一心仪对象 \(5\) 结了婚了！

我们再看一看 \(1\) ，发现他其实还可以和 \(6\) 结婚且 \(6\) 未婚。

邪恶的匈牙利算法便强制让 \(1\) 、 \(5\) 离婚以此给 \(2\) 找老婆！

太邪恶了！赤裸裸的包办婚姻！！！

再看 \(3\) ，却不曾想 \(3\) 有一心仪对象 \(6\) 结了婚了！

我们再看一看 \(1\) ，发现他其实和 \(5\) 还可以破镜重圆且 \(2\) 还可以和 \(7\) 结婚。

邪恶的匈牙利算法便又动了手脚：

\(1\)、\(5\)结婚，\(2\)、\(7\)结婚，\(3\)、\(6\)结婚

接下来到 \(4\) 了。很幸运，他可以直接和 \(8\) 结婚。

拆散婚姻什么的已经无所谓了，因为不再有姻缘，值得去拆了。——匈牙利算法

好了你已经掌握了匈牙利算法是个什么东西了。

接下来，也是最后一部分，就是喜闻乐见的上代码时间了：

(注：代码参考了我校一个老二刺猿学长 \(shadowice1984\)，即 \(tbl\) 的 )

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int N=510;
int n,m,e;
int mp[N][N],match[N];
bool book[N];
  
bool dfs(int x){
    for(int i=1;i<=m;i++){
	if(book[i]||!mp[x][i])
	    continue;
	book[i]=true;
	if(match[i]==0||dfs(match[i])){
	    match[i]=x;
	    return true;
	}
    }
    return false;
}
int main(){
	scanf("%d%d%d",&n,&m,&e);
	for(int i=1;i<=e;i++){
		int j;int k;
		scanf("%d%d",&j,&k);
		mp[j][k]=1;
	}
	int ans=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++)
			book[j]=false;
		ans+=dfs(i);
	}
	printf("%d",ans);
	return 0;
}