[洛谷P1600] 天天爱跑步
洛谷题目链接:天天爱跑步
题目描述
小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一一棵包含 \(n\)个结点和 \(n-1\)条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从\(1\)到\(n\)的连续正整数。
现在有\(m\)个玩家,第\(i\)个玩家的起点为 \(S_i\),终点为 \(T_i\) 。每天打卡任务开始时,所有玩家在第\(0\)秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)
小c想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点\(j\)的观察员会选择在第\(W_j\)秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第\(W_j\)秒也理到达了结点 \(j\) 。 小C想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点\(j\)作为终点的玩家: 若他在第\(W_j\)秒前到达终点,则在结点\(j\)的观察员不能观察到该玩家;若他正好在第\(W_j\)秒到达终点,则在结点\(j\)的观察员可以观察到这个玩家。
输入输出格式
输入格式:
第一行有两个整数\(n\)和\(m\) 。其中\(n\)代表树的结点数量, 同时也是观察员的数量, \(m\)代表玩家的数量。
接下来 \(n- 1\)行每行两个整数\(u\)和 \(v\),表示结点 \(u\)到结点 \(v\)有一条边。
接下来一行 \(n\)个整数,其中第\(j\)个整数为\(W_j\) , 表示结点jjj出现观察员的时间。
接下来 \(m\)行,每行两个整数\(S_i\),和\(T_i\),表示一个玩家的起点和终点。
对于所有的数据,保证\(1\leq S_i,T_i\leq n, 0\leq W_j\leq n\) 。
输出格式:
输出1行 \(n\)个整数,第\(j\)个整数表示结点\(j\)的观察员可以观察到多少人。
输入输出样例
输入样例#1:
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
输出样例#1:
2 0 0 1 1 1
输入样例#2:
5 3
1 2
2 3
2 4
1 5
0 1 0 3 0
3 1
1 4
5 5
输出样例#2:
1 2 1 0 1
说明
【样例1说明】
对于\(1\)号点,\(W_i=0\),故只有起点为1号点的玩家才会被观察到,所以玩家\(1\)和玩家\(2\)被观察到,共有\(2\)人被观察到。
对于\(2\)号点,没有玩家在第\(2\)秒时在此结点,共\(0\)人被观察到。
对于\(3\)号点,没有玩家在第\(5\)秒时在此结点,共\(0\)人被观察到。
对于\(4\)号点,玩家\(1\)被观察到,共\(1\)人被观察到。
对于\(5\)号点,玩家\(1\)被观察到,共\(1\)人被观察到。
对于\(6\)号点,玩家\(3\)被观察到,共\(1\)人被观察到。
【子任务】
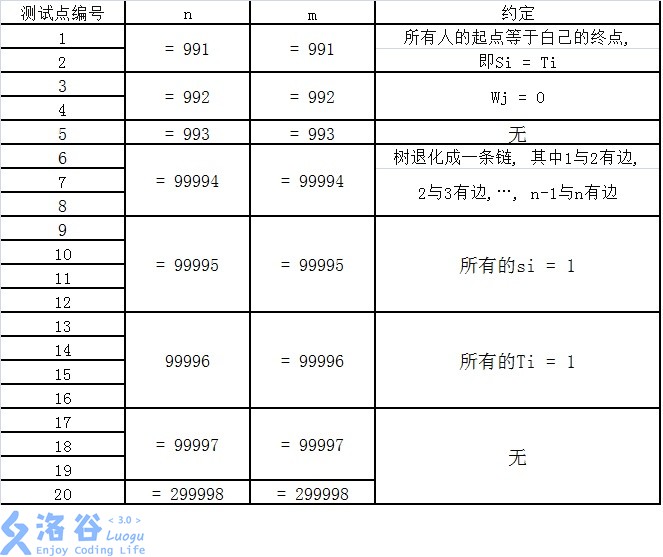
每个测试点的数据规模及特点如下表所示。 提示: 数据范围的个位上的数字可以帮助判断是哪一种数据类型。
题意: 一颗\(n\)个点的树上有\(m\)条路径,每条路径的起点有一个玩家,并且会在\(0\)时刻开始向终点走.每个点有一个观察员,他能观察到这个玩家当且仅当这个玩家在观察员出现的时候经过这个点.问每个观察员能观察到的玩家数量.
题解: 这道题我们先针对每一个部分分数据点来考虑.
pts10:所有人的起点等于终点
直接统计所有有玩家的位置,每个位置观察员出现时间为\(0\)就输出答案,否则输出\(0\).
pts10:\(W_j=0\)
直接统计所有玩家初始位置.
pts5:\(n=993,m=993\)
模拟玩家在路径上走的过程,对于一条路径,计算路径上每个观察员能否观察到这个玩家.
namespace pts25 {
int ans[N], dep[N], fa[N];
void dfs(int x, int f, int deep) {
dep[x] = deep, fa[x] = f;
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != fa[x]) dfs(e[i].to, x, deep+1);
}
int lca(int x, int y) {
if(dep[x] < dep[y]) swap(x, y);
while(dep[x] > dep[y]) x = fa[x];
while(x != y) x = fa[x], y = fa[y];
return x;
}
void check(int x, int y) {
int LCA = lca(x, y), size = dep[x]+dep[y]-dep[LCA]*2+1, cnt = 0, cnt1 = 0;
for(; x != LCA; x = fa[x], cnt++, cnt1++)
if(come[x] == cnt) ans[x]++;
if(come[LCA] == cnt++) ans[LCA]++;
size = size-cnt+cnt1;
for(; y != LCA; y = fa[y], size--)
if(come[y] == size) ans[y]++;
}
void work() {
dfs(1, -1, 1);
for(int i = 1; i <= m; i++) check(a[i].x, a[i].y);
for(int i = 1; i <= n; i++) printf("%d ", ans[i]);
printf("\n");
exit(0);
}
}
pts15:树退化成一条链
将向左走和向右走分开统计(下面默认向右走).
考虑对于一个观察员\(i\)观察到某个玩家\(j\)的条件,发现只有当玩家的出发点\(st_j=i-come[i]\)的时候才能被观察到,其中\(come[i]\)为第\(i\)个观察员观察的时间.可以自己画图理解一下.
namespace pts_chain {
int b[N], ans[N], cnt1 = 0, cnt2 = 0;
struct node {
int pos, upd, val;
} upd1[N*2], upd2[N*2];
bool cmp1(node a, node b) { return a.pos < b.pos; }
bool cmp2(node a, node b) { return a.pos > b.pos; }
void work() {
for(int i = 1; i <= m; i++)
if(a[i].x == a[i].y && come[a[i].x] == 0) ans[a[i].x]++;
for(int i = 1; i <= m; i++) {
if(a[i].x < a[i].y) {
upd1[++cnt1] = (node) { a[i].x, a[i].x, 1 };
upd1[++cnt1] = (node) { a[i].y+1, a[i].x, -1 };
}
if(a[i].x > a[i].y) {
upd2[++cnt2] = (node) { a[i].x, a[i].x, 1 };
upd2[++cnt2] = (node) { a[i].y-1, a[i].x, -1 };
}
}
sort(upd1+1, upd1+cnt1+1, cmp1), sort(upd2+1, upd2+cnt2+1, cmp2);
for(int i = 1, pos = 1; i <= n; i++) {
for(; pos <= cnt1 && upd1[pos].pos <= i; pos++)
b[upd1[pos].upd] += upd1[pos].val;
ans[i] += b[i-come[i]];
}
for(int i = n, pos = 1; i >= 1; i--) {
for(; pos <= cnt2 && upd2[pos].pos >= i; pos++) {
b[upd2[pos].upd] += upd2[pos].val;
}
ans[i] += b[i+come[i]];
}
for(int i = 1; i <= n; i++) printf("%d ", ans[i]);
printf("\n");
exit(0);
}
}
所有的\(S_i=1\)
因为所有起点都是\(1\),所以所有玩家可以看作是同时从\(1\)节点出发,这样他们的时间轴就是统一的了.一个观察员要观察到一个玩家,那么这个观察员所在的深度\(dep[i]=come[i]\),其中\(1\)节点的深度为\(0\).如果不满足这个条件,一定是没有玩家可以被他观察到的,因为所有玩家的起点都是\(1\),并都会向下走,所以到达某个深度的时间就是这个深度.
那么这样我们就可以用树上差分来统计一下树上的路径被经过了多少次,然后一次\(dfs\)统计差分,最后如果深度等于观察时间的观察员就输出统计的次数,否则输出\(0\).
namespace pts_si1 {
int ans[N], dep[N];
void dfs(int x, int f, int deep) {
dep[x] = deep;
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs(e[i].to, x, deep+1), ans[x] += ans[e[i].to];
}
void work(path a[], int m) {
for(int i = 1; i <= m; i++) ans[a[i].y]++;
dfs(1, -1, 0);
for(int i = 1; i <= n; i++) {
if(come[i] == dep[i]) printf("%d ", ans[i]);
else printf("0 ");
}
exit(0);
}
}
所有的\(T_i=1\)
其实这个部分分的做法像是暴力模拟的做法和所有\(S_i=1\)的做法的组合.
同样的我们考虑统计一个观察员\(i\)如何才能观察到玩家\(j\).要使\(i\)能观察到\(j\),则有\(dep[j]-dep[i]=come[i]\),将\(i,j\)分开放,则有\(dep[i]+come[i]=dep[j]\),也就是说,我们在统计差分数组的时候,对于某一个点\(i\),它能观察到的所有节点是它子树中深度为\(dep[i]+come[i]\)的个数.这个统计我们同样可以用树上差分实现.
但是在统计的过程中,因为我们需要将一个节点子节点的桶的状态传向父节点,而这样就会有可能在统计的时候统计到别的子树中去,所以我们需要先减去之前状态所造成的贡献,然后在统计完这个节点后再给答案加上这颗子树的贡献.
namespace pts_ti1 {
int ans[N], dep[N], b[N], upd[N];
void dfs(int x, int f, int deep) {
dep[x] = deep, ans[x] -= b[come[x]+dep[x]];
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs(e[i].to, x, deep+1);
b[dep[x]] += upd[x];
ans[x] += b[come[x]+dep[x]];
}
void work(path a[], int m) {
for(int i = 1; i <= m; i++) upd[a[i].x]++;
dfs(1, -1, 0);
for(int i = 1; i <= n; i++) printf("%d ", ans[i]);
printf("\n");
exit(0);
}
}
下面来讲一下满分做法.
其实如果所有部分分都会写了,正解就很简单了
其实对于一个玩家的路径,我们可以拆成一条向上的路径和一条向下的路径,只不过它的起点/终点不是\(1\).这时候,我们就需要给树上的贡献差分一下.也就是对于一条路径(默认向上走)\((x->y)\),我们需要在\(x\)点加入这条路径的贡献,然后需要在\(fa[y]\)的地方减去这个贡献,防止贡献被多次统计.
而这样统计的话,我们就会有一个问题:在\(fa[y]\)修改的贡献仍然是\(x\)点所造成的贡献,也就是说,一个点可能有多条路径作贡献,所以这里我们可以采用一个\(vector\)存下一个点的所有贡献.然后在\(dfs\)统计差分数组的时候将一个点的贡献全部加入差分数组中,其他的操作和之前写部分分的方法是一样的.
如果有过程不太理解的可以重新看一下各部分分的解法,最后整合的时候注意一下细节,这道题码量感觉还是有点大的,要耐心打.
namespace pts100 {
int ans[N], anss[N], anst[N], dep[N], gup[N][25], bs[N*2], bt[N];
struct node { int pos, val; };
vector <node> upds[N], updt[N];
void dfs(int x, int f, int deep) {
gup[x][0] = f, dep[x] = deep;
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs(e[i].to, x, deep+1);
}
void init() {
for(int j = 1; j <= 23; j++)
for(int i = 1; i <= n; i++) gup[i][j] = gup[gup[i][j-1]][j-1];
}
int lca(int a, int b) {
if(dep[a] < dep[b]) swap(a, b);
for(int i = 23; i >= 0; i--)
if(dep[gup[a][i]] >= dep[b]) a = gup[a][i];
if(a == b) return a;
for(int i = 23; i >= 0; i--)
if(gup[a][i] != gup[b][i]) a = gup[a][i], b = gup[b][i];
return gup[a][0];
}
void dfs_s(int x, int f) {
anss[x] -= bs[come[x]-dep[x]+N];
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs_s(e[i].to, x);
for(int i = 0; i < upds[x].size(); i++)
bs[upds[x][i].pos+N] += upds[x][i].val;
anss[x] += bs[come[x]-dep[x]+N];
}
void dfs_t(int x, int f) {
anst[x] -= bt[come[x]+dep[x]];
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs_t(e[i].to, x);
for(int i = 0; i < updt[x].size(); i++)
bt[updt[x][i].pos] += updt[x][i].val;
anst[x] += bt[come[x]+dep[x]];
}
void work(path a[], int m) {
dep[0] = -1, dfs(1, 0, 0), init();
for(int i = 1; i <= m; i++) {
int LCA, size;
LCA = lca(a[i].x, a[i].y);
size = dep[a[i].x]+dep[a[i].y]-dep[LCA]*2+1;
if(a[i].x == a[i].y) {
if(!come[a[i].x]) ans[a[i].x]++;
continue;
}
updt[a[i].x].push_back((node) { dep[a[i].x], 1 }); // going up
updt[gup[LCA][0]].push_back((node) { dep[a[i].x], -1 });
upds[a[i].y].push_back((node) { size-dep[a[i].y]-1, 1 });
upds[LCA].push_back((node) { size-dep[a[i].y]-1, -1 }); // going down
}
dfs_s(1, 0); dfs_t(1, 0);
for(int i = 1; i <= n; i++) printf("%d ", ans[i]+anss[i]+anst[i]);
printf("\n");
exit(0);
}
}
最后贴一个全部分分整合的代码吧.
#include<bits/stdc++.h>
using namespace std;
const int N = 299998+5;
int n, m, last[N], come[N], ecnt = 0;
struct edge{
int to, nex;
}e[N*2];
struct path{
int x, y;
}a[N];
int gi(){
int res = 0, f = 1; char i = getchar();
while(i < '0' || i > '9'){ if(i == '-') f = -1; i = getchar(); }
while(i >= '0' && i <= '9') res = res*10+i-'0', i = getchar();
return res*f;
}
void add(int x, int y){
e[++ecnt].to = y, e[ecnt].nex = last[x], last[x] = ecnt;
}
namespace pts25{
int ans[N], dep[N], fa[N];
void dfs(int x, int f, int deep){
dep[x] = deep, fa[x] = f;
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != fa[x]) dfs(e[i].to, x, deep+1);
}
int lca(int x, int y){
if(dep[x] < dep[y]) swap(x, y);
while(dep[x] > dep[y]) x = fa[x];
while(x != y) x = fa[x], y = fa[y];
return x;
}
void check(int x, int y){
int LCA = lca(x, y), size = dep[x]+dep[y]-dep[LCA]*2+1, cnt = 0, cnt1 = 0;
for(; x != LCA; x = fa[x], cnt++, cnt1++)
if(come[x] == cnt) ans[x]++;
if(come[LCA] == cnt++) ans[LCA]++; size = size-cnt+cnt1;
for(; y != LCA; y = fa[y], size--)
if(come[y] == size) ans[y]++;
}
void work(){
dfs(1, -1, 1);
for(int i = 1; i <= m; i++) check(a[i].x, a[i].y);
for(int i = 1; i <= n; i++) printf("%d ", ans[i]); printf("\n");
exit(0);
}
}
namespace pts_chain{
int b[N], ans[N], cnt1 = 0, cnt2 = 0;
struct node{
int pos, upd, val;
}upd1[N*2], upd2[N*2];
bool cmp1(node a, node b){ return a.pos < b.pos; }
bool cmp2(node a, node b){ return a.pos > b.pos; }
void work(){
for(int i = 1; i <= m; i++)
if(a[i].x == a[i].y && come[a[i].x] == 0) ans[a[i].x]++;
for(int i = 1; i <= m; i++){
if(a[i].x < a[i].y){
upd1[++cnt1] = (node){ a[i].x, a[i].x, 1 };
upd1[++cnt1] = (node){ a[i].y+1, a[i].x, -1 };
}
if(a[i].x > a[i].y){
upd2[++cnt2] = (node){ a[i].x, a[i].x, 1 };
upd2[++cnt2] = (node){ a[i].y-1, a[i].x, -1 };
}
}
sort(upd1+1, upd1+cnt1+1, cmp1), sort(upd2+1, upd2+cnt2+1, cmp2);
for(int i = 1, pos = 1; i <= n; i++){
for(; pos <= cnt1 && upd1[pos].pos <= i; pos++)
b[upd1[pos].upd] += upd1[pos].val;
ans[i] += b[i-come[i]];
}
for(int i = n, pos = 1; i >= 1; i--){
for(; pos <= cnt2 && upd2[pos].pos >= i; pos++){
cerr << upd2[pos].upd << endl;
b[upd2[pos].upd] += upd2[pos].val;
}
ans[i] += b[i+come[i]];
}
for(int i = 1; i <= n; i++) printf("%d ", ans[i]); printf("\n");
exit(0);
}
}
namespace pts_si1{
int ans[N], dep[N];
void dfs(int x, int f, int deep){
dep[x] = deep;
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs(e[i].to, x, deep+1), ans[x] += ans[e[i].to];
}
void work(path a[], int m){
for(int i = 1; i <= m; i++) ans[a[i].y]++;
dfs(1, -1, 0);
for(int i = 1; i <= n; i++){
if(come[i] == dep[i]) printf("%d ", ans[i]);
else printf("0 ");
}
exit(0);
}
}
namespace pts_ti1{
int ans[N], dep[N], b[N], upd[N];
void dfs(int x, int f, int deep){
dep[x] = deep, ans[x] -= b[come[x]+dep[x]];
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs(e[i].to, x, deep+1);
b[dep[x]] += upd[x];
ans[x] += b[come[x]+dep[x]];
}
void work(path a[], int m){
for(int i = 1; i <= m; i++) upd[a[i].x]++;
dfs(1, -1, 0);
for(int i = 1; i <= n; i++) printf("%d ", ans[i]); printf("\n");
exit(0);
}
}
namespace pts100{
int ans[N], anss[N], anst[N], dep[N], gup[N][25], bs[N*2], bt[N];
struct node{ int pos, val; };
vector <node> upds[N], updt[N];
void dfs(int x, int f, int deep){
gup[x][0] = f, dep[x] = deep;
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs(e[i].to, x, deep+1);
}
void init(){
for(int j = 1; j <= 23; j++)
for(int i = 1; i <= n; i++) gup[i][j] = gup[gup[i][j-1]][j-1];
}
int lca(int a, int b){
if(dep[a] < dep[b]) swap(a, b);
for(int i = 23; i >= 0; i--)
if(dep[gup[a][i]] >= dep[b]) a = gup[a][i];
if(a == b) return a;
for(int i = 23; i >= 0; i--)
if(gup[a][i] != gup[b][i]) a = gup[a][i], b = gup[b][i];
return gup[a][0];
}
void dfs_s(int x, int f){
anss[x] -= bs[come[x]-dep[x]+N];
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs_s(e[i].to, x);
for(int i = 0; i < upds[x].size(); i++)
bs[upds[x][i].pos+N] += upds[x][i].val;
anss[x] += bs[come[x]-dep[x]+N];
}
void dfs_t(int x, int f){
anst[x] -= bt[come[x]+dep[x]];
for(int i = last[x]; i; i = e[i].nex)
if(e[i].to != f) dfs_t(e[i].to, x);
for(int i = 0; i < updt[x].size(); i++)
bt[updt[x][i].pos] += updt[x][i].val;
anst[x] += bt[come[x]+dep[x]];
}
void work(path a[], int m){
dep[0] = -1, dfs(1, 0, 0), init();
for(int i = 1; i <= m; i++){
int LCA, size; LCA = lca(a[i].x, a[i].y);
size = dep[a[i].x]+dep[a[i].y]-dep[LCA]*2+1;
if(a[i].x == a[i].y){ if(!come[a[i].x]) ans[a[i].x]++; continue; }
updt[a[i].x].push_back((node){ dep[a[i].x], 1 }); // going up
updt[gup[LCA][0]].push_back((node){ dep[a[i].x], -1 });
upds[a[i].y].push_back((node){ size-dep[a[i].y]-1, 1 });
upds[LCA].push_back((node){ size-dep[a[i].y]-1, -1 }); // going down
}
dfs_s(1, 0); dfs_t(1, 0);
for(int i = 1; i <= n; i++) printf("%d ", ans[i]+anss[i]+anst[i]);
printf("\n");
exit(0);
}
}
int main(){
int x, y; n = gi(), m = gi();
for(int i = 1; i < n; i++)
x = gi(), y = gi(), add(x, y), add(y, x);
for(int i = 1; i <= n; i++) come[i] = gi();
for(int i = 1; i <= m; i++) a[i].x = gi(), a[i].y = gi();
//if(n <= 993) pts25::work();
//if(n == 99994) pts_chain::work();
//if(n == 99995) pts_si1::work(a, m);
//if(n == 99996) pts_ti1::work(a, m);
pts100::work(a, m);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号