TREAP
TREAP
Treap = Tree + Heap.
树堆,在数据结构中也称Treap,是指有一个随机附加域满足堆的性质的二叉搜索树,其结构相当于以随机数据插入的二叉搜索树。其基本操作的期望时间复杂度为O(logn)。相对于其他的平衡二叉搜索树,Treap的特点是实现简单,且能基本实现随机平衡的结构。
Treap 维护堆的性质的方法只用到了左旋和右旋, 编程复杂度比Splay小一点(??), 并且在两者可完成的操作速度有明显优势
然而一个裸的treap是不能支持区间操作的,所以可能功能没有splay那么强大.
treap的操作方式和splay差不多,但因为treap的结构是不能改变的,而splay的形态可以随意改变,所以在实现上会有一点小区别.
treap具有以下性质:
- Treap是关于key的二叉排序树(也就是规定的排序方式)。
- Treap是关于priority的堆(按照随机出的优先级作为小根/大根堆)。(非二叉堆,因为不是完全二叉树)
- key和priority确定时,treap唯一。
为什么除了权值还要在用一个随机值作为排序方法呢?随机分配的优先级,使数据插入后更不容易退化为链。就像是将其打乱再插入。所以用于平衡二叉树。
首先是treap的定义:
struct treap{
int ch[2], cnt, size, val, rd;
//treap不需要记录父指针,rd表示节点的随机值
}t[N];
更新
直接统计子树大小.
void up(int x){
t[x].size = t[t[x].ch[0]].size+t[t[x].ch[1]].size+t[x].cnt;
}
旋转
treap需要支持平衡树的性质,所以是需要用到旋转的.这里旋转的方法是和splay的旋转方法是一样的,就不贴图了.因为treap中并没有记录父节点,所以需要传一个参数表示旋转方向.
void rotate(int &x, int d){//x代表的是旋转时作为父节点的节点,d代表的是旋转的方向
//d==0时是左儿子旋上来, d==1是右儿子旋上来.
int son = t[x].ch[d];
t[x].ch[d] = t[son].ch[d^1];
t[son].ch[d^1] = x; up(x), up(x=son);//相当于up(son)
}
插入/删除
因为treap在其他操作过程中是并不改变树的形态的,所以在插入或是删除时要先找到要插入/删除的节点的位置,然后再创建一个新的节点/删除这个节点.
然后考虑到插入/删除后树的形态有可能会改变,所以要考虑要通过旋转维护treap的形态.我们这里分类讨论一下:
插入
- 可以直接按照中序遍历结果找到最终的对应位置,然后再通过随机值维护它堆的性质.
void insert(int &x, int val){
if(!x){//找到对应位置就新建节点
x = ++cnt;
t[x].cnt = t[x].size = 1;
t[x].val = val, t[x].rd = rand();
return;
}
t[x].size++;//因为插入了数,所以在路径上每个节点的size都会加1
if(t[x].val == val){t[x].cnt++; return;}//找到了直接返回
int d = t[x].val < val; insert(t[x].ch[d], val);//否则递归查找插入位置
if(t[x].rd > t[t[x].ch[d]].rd) rotate(x, d);
}
删除
- 先找到要删除的节点的位置.
- 如果这个节点位置上有多个相同的数,则直接cnt--.
- 如果只有一个儿子或者没有儿子,直接将那个儿子接到这个节点下面(或将儿子赋值为0).
- 如果有两个儿子,现将随机值小的那个旋到这个位置,将根旋下去,然后将旋之后的情况转化为前几种情况递归判断.
void delet(int &x, int val){
if(!x) return;//防止越界
if(t[x].val == val){
if(t[x].cnt > 1){t[x].cnt--, t[x].size--;return;}//有相同的就直接cnt--
bool d = t[ls].rd > t[rs].rd;
if(ls == 0 || rs == 0) x = ls+rs;//只有一个儿子就直接把那个儿子放到这个位置
else rotate(x, d), delet(x, val);//否则将x旋下去,找一个随机值小的替代,直到回到1,2种情况
}
else t[x].size--, delet(t[x].ch[t[x].val<val], val);//递归找到要删除的节点.
}
查排名
还是因为treap不能改变形态,所以不能像splay一样直接找到这个点旋转到根,所以我们用递归的方式求解,我们用到的目前这个点的权值作为判断的依据,并在找到节点的路上不断累加小于该权值的个数.
看代码理解一下吧.
int rank(int x, int val){
if(!x) return 0;
if(t[x].val == val) return t[ls].size+1;//找到了就返回最小的那个
if(t[x].val > val) return rank(ls, val);//如果查找的数在x的左边,则直接往左边查
return rank(rs, val)+t[ls].size+t[x].cnt;//否则往右边查,左边的所有数累加进答案
}
查找第k小的数
因为只需要找到中序遍历中的第k个,所以在找第k小的时候可以直接用splay一样的方法,也是递归求解.
int kth(int root, int k){
int x = root;
while(1){
if(k <= t[ls].size) x = ls;
else if(k > t[ls].size+t[x].cnt)
k -= t[ls].size+t[x].cnt, x = rs;
else return t[x].val;
}
}
查找前驱/后继
仍然是因为不能改变树的形态,需要递归求解.同样的找一个节点的前驱就直接在它左半边中找一个最大值就可以了.如果是在这个节点的右边的话就一直向下递归,如果递归有一个分支直到叶子节点以下都一直没找到一个比该权值要小的值,那么最后要返回一个-inf/inf来防止答案错误(同时找到叶子节点下面也是要及时return防止越界).
int pre(int x, int val){
if(!x) return -inf;//防止越界,同时-inf无法更新答案,
if(t[x].val >= val) return pre(ls, val);//如果该节点的权值大于等于要找的权值
//则不能成为前驱,递归查找左子树(有可能找到前驱)
return max(pre(rs, val), t[x].val);//找右子树中是否存在前驱
}
int nex(int x, int val){//同上
if(!x) return inf;
if(t[x].val <= val) return nex(rs, val);
return min(nex(ls, val), t[x].val);
}
既然treap有这么多不能实现的操作,那这个treap有什么用呢?
显然是有的,我们因为支持旋转的treap不能改变树的形态来完成操作,所以这里介绍一中更加强大的数据结构:
无旋treap
简介
无旋treap具有treap的一些性质,比如二叉树和堆的性质,同时也是一颗平衡树.
无旋treap是怎么个无旋的方法的呢?其实相比于带旋转的treap,无旋treap只是多了两个特殊的操作:split 和merge .
那么这两个操作到底是什么这么厉害呢?说简单点,就是一个分离子树和一个合并子树的过程.
我们可以用split操作分离出1~前k个节点,这样就可以通过两次split操作就可以提取出任意一段区间了.
而merge操作可以将两个子树合并,并同时维护好新合并的树的treap所有的性质.
下面终点讲一下这两个操作:
split
首先看一张split的动图:

操作过程如上,节点中间的值代表权值,右边的数字代表随机值.
我们在操作的过程中需要将一颗树剖成两颗,然后为了还能进行之后的操作,分离出的两颗字数必须也是满足性质的,为了找到这两颗子树,我们在分离的过程中需要记录下这两颗子树的根.
从图中可以看出,其实这个分离的操作也可以理解为将一棵树先剖开,然后再按照一定的顺序连接起来,也就是将从x节点一直到最坐下或是最右下剖出来,然后再继续处理剖出来链的剩余部分.
看代码理解一下吧.
void split(int x, int k, int &a, int &b){//开始时a,b传的是用来记录两颗子树根的变量
//x代表目前操作到了哪一个节点,k是要分离出前k个节点
if(!x){a = b = 0; return;}//如果没有节点则需要返回
if(k <= t[ls].size) b = x, split(ls, k, a, ls);//如果第k个在左子树中
//则往左走,同时左子树的根就可以确定了,那么就把ls赋值为根.
//同时为了之后要把接下来处理出的节点再连上去,要再传ls作为参数,将之后改变为根的接到现在的x的左儿子
else a = x, split(rs, k-t[ls].size-1, rs, b);//同理
}
当然,要实现查找前驱后继的话可以不用分离前k个节点的方法来分离,可以直接按照权值来分离节点,方法类似.
void split(int x, int val, int &a, int &b){
if(!x){a = b = 0; return;}
if(t[x].val <= val) a = x, split(rs, val, rs, b);
//如果带等于就是把>val的节点分到第二颗子树中.
//否则就是将<=val的节点分到第一颗子树中.
else b = x, split(ls, val, a, ls); up(x);
}
merge

注:图中最后插入的9位置错了,应该是在8的右下.
首先merge操作是有前提条件的,要求是必须第一颗树权值最大的节点要大于第二棵树权值最小的节点.
因为有了上面那个限制条件,所以右边的子树只要是插在左边的这颗树的右儿子上就可以维护它的中序遍历,那么我们就只需要考虑如何维护它平衡树的性质.
这里我们就需要通过玄学的随机值来维护这个树的性质了.我们在合并两颗树时,因为左边的权值是一定小于右边的,所以左边的那棵树一定是以一个根和它的左子树的形式合并的,而右边的那棵树就是以根和右子树的形式合并的,那么如果这次选择的是将左边的树合并上来的话,那么下一次合并过来的位置一定是在这个节点位置的右儿子位置(可以看图理解一下).
你可以把这个过程理解为在第一个Treap的左子树上插入第二个树,也可以理解为在第二个树的左子树上插入第一棵树。因为第一棵树都满足小于第二个树,所以就变成了比较随机值来确定树的形态。
int merge(int x, int y){
if(x == 0 || y == 0) return x+y;
if(t[x].rd < t[y].rd){//最好merge函数不要用宏定义的变量
//因为这个比较的两颗树的根的随机值,用宏定义容易写错
t[x].ch[1] = merge(t[x].ch[1], y);
up(x); return x;
}
else {
t[y].ch[0] = merge(x, t[y].ch[0]);
up(y); return y;
}
}
到这里两个核心操作就完成了,那么那些insert,delete,get_rank,get_pre,get_nex的操作该怎么做呢?其实很简单,就考虑一下将这颗树如何分离,然后重新合并好就可以了.
插入
插入还是老套路,先找到位置然后插入.这里我们可以先分离出val和它之前的节点,然后把val权值的节点加到第一颗树的后面,然后合并.
void insert(int val){
split(root, val, r1, r2);
root = merge(r1, merge(newnode(val), r2));
}
至于newnode的话就直接新建一个节点就可以了.
int newnode(int val){
t[++cnt].val = val; t[cnt].rd = rand(), t[cnt].size = 1;
return cnt;
}
删除
先将val和它前面的权值分离出来,用r1记录这个根,再在r1树中分离出val-1的权值的树,用r2记录这颗树,那么val这个权值一定是已经被分离到以r2为根的树中,删掉这个数(可以直接把这个位置的节点用它左右儿子合并后的根代替),最后将分离的这几颗树按顺序合并回去就可以了.
void delet(int val){
r1 = r2 = r3 = 0; split(root, val, r1, r3);
split(r1, val-1, r1, r2);
r2 = merge(t[r2].ch[0], t[r2].ch[1]);
root = merge(r1, merge(r2, r3));
}
查找某数的排名
可以直接将所有比它小的权值分离到一颗树中,那么此时排名就是这颗树的大小+1了.
int rank(int val){
r1 = r2 = 0; split(root, val-1, r1, r2);
ans = t[r1].size+1;
root = merge(r1, r2);
return ans;
}
查找第k小的数
可以直接在整颗树中直接找,操作方法类似splay.
int kth(int rt, int k){
int x = rt;
while(1){
if(k <= t[ls].size) x = ls;
else if(k > t[ls].size+t[x].cnt)
k -= t[ls].size+t[x].cnt, x = rs;
else return x;
}
}
查找前驱/后继
以val-1为分界线将整棵树分离开,那么前驱就是第一颗树中的最大的数字(严格比val小).
以val为分界线将整颗树分离开,后继就是第二颗树中的最小的数字(严格比val大).
int pre(int val){
r1 = r2 = 0; split(root, val-1, r1, r2);
ans = t[kth(r1, t[r1].size)].val;
root = merge(r1, r2);
return ans;
}
int nex(int val){
r1 = r2 = 0; split(root, val, r1, r2);
ans = t[kth(r2, 1)].val;
root = merge(r1, r2);
return ans;
}
通过节点编号找节点在中序遍历中的位置
因为treap本身是不能通过编号来进行操作的,它只能通过\(split\)来分离子树,所以在只知道节点编号的时候不能很快找到节点的位置.
所以为了方便寻找节点.我们在treap中多记录一个\(father\),然后就可以通过不断的向上跳来记录中序遍历比它小的节点的个数.
而中序遍历比它小的节点也就是在它左子树中的节点或是在它祖先的左子树中的节点.我们只需要在向根跳的时候将所有左子树记录下来就可以了.但是因为有可能某个节点是根的左儿子,这样在向上跳的时候就不用重复统计答案了.
int find(int cnt){
int node = cnt, res = t[t[cnt].ch[0]].size+1;
while(node != root && cnt){
if(get(cnt)) res += t[t[t[cnt].fa].ch[0]].size+1;
cnt = t[cnt].fa;
}
return res;
}
然后我们需要考虑\(father\)的修改.因为会改变树的形态的只有\(split\)和\(merge\)操作,所以只需要在这两个函数进行修改就可以了.其实很简单,只要在修改儿子的同时修改父亲就可以了.
\(split\)
void split(int x, int k, int &a, int &b, int faa = 0, int fab = 0){
if(x == 0){ a = b = 0; return; }
if(k <= t[t[x].ch[0]].size) t[x].fa = fab, b = x, split(t[x].ch[0], k, a, t[x].ch[0], faa, x);
else t[x].fa = faa, a = x, split(t[x].ch[1], k-t[t[x].ch[0]].size-1, t[x].ch[1], b, x, fab); up(x);
}
\(merge\)
int merge(int x, int y){
if(x == 0 || y == 0) return x+y;
if(t[x].rd < t[y].rd){
t[x].ch[1] = merge(t[x].ch[1], y);
t[t[x].ch[1]].fa = x; up(x); return x;
}
else {
t[y].ch[0] = merge(x, t[y].ch[0]);
t[t[y].ch[0]].fa = y; up(y); return y;
}
}
如何在\(O(n)\)时间内构造一颗平衡treap
可以考虑用栈实现.
每次将一个节点压入栈中,为了满足构造的这颗平衡树的中序遍历是按照我们的输入顺序的,所以每次插入的节点一定是在之前构造的部分的右边的.
所以这里用了一个栈,每次加入一个节点就把新节点编号加入栈.并且栈中的元素都在栈的右边.
简单点说,也就是如果不考虑这个随机值的话,构造的平衡树就是一条链.从栈顶到栈底是一条从下到上的链,像这样:
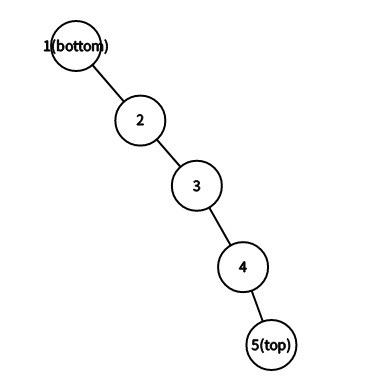
但是我们显然是不能让它构造一条链的,所以我们通过随机值来判断什么时候要将这条链缩短,并把这条链接到新的根的右儿子上.我们再假设现在已经插入了4个数,并且随机值正好是满足它成为一条链的情况的,那么该如何插入5呢?(节点边上的括号内的值是随机值).
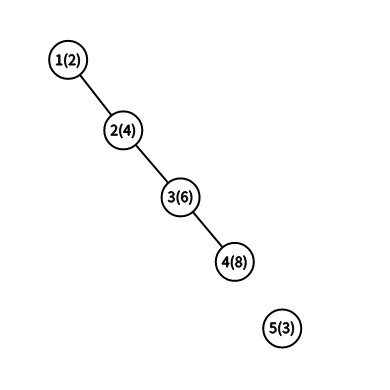
显然按照随机值维护堆的性质的原理,5节点应该是要到1节点的下面的,那么那一重\(while\)循环就会进行判断,并保存\(last\)最后到哪个位置.(如下图)
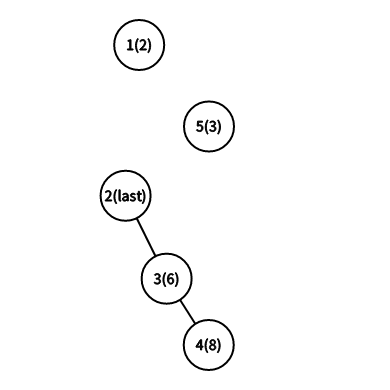
显然我们这样可以将一条链分开来,并且不会改变它原有的链.最后将节点按顺序接上,这样新插入一个节点就完成了.
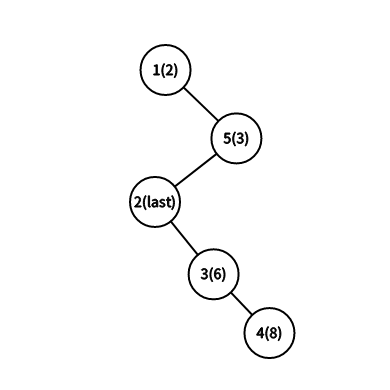
之后每次插入节点都是这个方法,这样造出的平衡树也是相对平衡的(随机值保证了树平衡的性质).
复杂度的话虽然里面套了个\(while\),但是每个点都是只会入栈出栈一次的,所以均摊下来是\(O(n)\)的.
int build(int len){
for(int i=1;i<=len;i++){
int temp = newnode(s[i]), last = 0;
while(top && t[stk[top]].rd > t[temp].rd)
up(stk[top]), last = stk[top], stk[top--] = 0;
if(top) t[stk[top]].ch[1] = temp;
t[temp].ch[0] = last, stk[++top] = temp;
}
while(top) up(stk[top--]); return stk[1];
}
总结
无旋treap到这里就差不多讲完了,感觉这个确实是很好用的,起码这个调试难度比其他的平衡树要简单一些.
分离区间什么的操作也是这个道理,可以自己想一下.
例题当然还是跳到这里看呀.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号