[洛谷P1126] 机器人搬重物

洛谷题目链接:机器人搬重物

题目描述

机器人移动学会（RMI）现在正尝试用机器人搬运物品。机器人的形状是一个直径1.6米的球。在试验阶段，机器人被用于在一个储藏室中搬运货物。储藏室是一个N*M的网格，有些格子为不可移动的障碍。机器人的中心总是在格点上，当然，机器人必须在最短的时间内把物品搬运到指定的地方。机器人接受的指令有：向前移动1步（Creep）；向前移动2步（Walk）；向前移动3步（Run）；向左转（Left）；向右转（Right）。每个指令所需要的时间为1秒。请你计算一下机器人完成任务所需的最少时间。

输入输出格式

输入格式：

输入的第一行为两个正整数N,M（N,M<=50），下面N行是储藏室的构造，0表示无障碍，1表示有障碍，数字之间用一个空格隔开。接着一行有四个整数和一个大写字母，分别为起始点和目标点左上角网格的行与列，起始时的面对方向（东E，南S，西W，北N），数与数，数与字母之间均用一个空格隔开。终点的面向方向是任意的。

输出格式：

一个整数，表示机器人完成任务所需的最少时间。如果无法到达，输出-1。

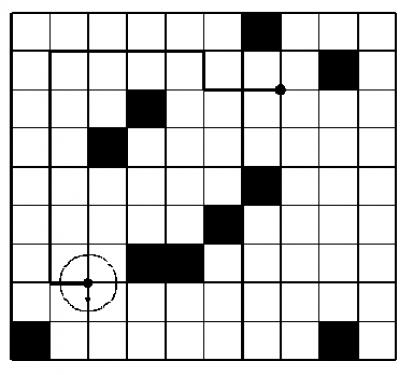
输入输出样例

输入样例#1：

9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 S

输出样例#1：

12

---

一道广搜的练习题.
注意一下细节:

• 边界条件为\((x,y),x\in[1,n),y\in[1,m)\).
• 机器人的大小会占用4个格子,给出的起点终点坐标的为这4个格子的左上的那个.
• 要判断好起点不能出发的情况.
• 走三格的时候要判断路径上是否都能走.
• 千万不要搞错了东西南北!!! 之前搞错这玩意调了快两天

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
const int N=50+5;

int n, m;
int a[N][N];
bool vis[N][N][5];//positions and directions
int step[N][N][5];
char dire;

struct node{
    int x, y, pos, dir;//1 -> East, 2 -> South, 3 -> West, 4 -> North
}st, ed;

int gi(){
    int ans = 0, f = 1; char i = getchar();
    while(i<'0'||i>'9'){if(i=='-')f=-1;i=getchar();}
    while(i>='0'&&i<='9'){ans=ans*10+i-'0';i=getchar();}
    return ans * f;
}

node change(node x,int f){
    node t = x;
    if(f == 4){t.dir = x.dir%4+1; return t;}//turn left
    if(f == 5){t.dir = (x.dir==1?4:(x.dir-1)); return t;}//turn right
    if(t.dir == 1) t.y += f;
    if(t.dir == 2) t.x += f;
    if(t.dir == 3) t.y -= f;
    if(t.dir == 4) t.x -= f;
    return t;
}

bool ok(node now,node nx){
    if(nx.x<1 || nx.x>=n || nx.y<1 || nx.y>=m) return false;
    if(a[nx.x][nx.y] || a[nx.x+1][nx.y] || a[nx.x][nx.y+1] || a[nx.x+1][nx.y+1]) return false;
    if(vis[nx.x][nx.y][nx.dir]) return false;
    int s = now.x, e = nx.x, f = 1;
    if(s == e) s = now.y, e = nx.y, f = 0;
    if(s > e) swap(s,e);
    if (e-s > 3) puts("error");
    if(f){
    for(int i=s;i<=e;i++)
        if(a[i][nx.y] || a[i][nx.y+1]) return false;
    }
    else
    for(int i=s;i<=e;i++)
        if(a[nx.x][i] || a[nx.x+1][i]) return false;
    return true;
}

void bfs(){
    queue <node> q; node now, nx; int flag = 0;
    q.push(st); vis[st.x][st.y][st.dir] = 1;
    while(!q.empty()){
	    now = q.front(); q.pop();
	    if(now.x == ed.x && now.y == ed.y){flag = 1; break;}
	    for(int i=1;i<=5;i++){
	        nx = change(now,i);
	        if(!ok(now,nx)) continue;
	        vis[nx.x][nx.y][nx.dir] = 1;
	        step[nx.x][nx.y][nx.dir] = step[now.x][now.y][now.dir]+1;
	        q.push(nx);
	    }
	}
    if(flag) printf("%d\n",step[now.x][now.y][now.dir]);
    else printf("-1\n");
}

int main(){
    //freopen("data.in","r",stdin);
    n = gi(); m = gi();
    for(int i=1;i<=n;i++)
	    for(int j=1;j<=m;j++)
	        a[i][j] = gi();
    st.x = gi(); st.y = gi();
    ed.x = gi(); ed.y = gi();
    cin >> dire;
    if(dire == 'E') st.dir = 1;
    if(dire == 'S') st.dir = 2;
    if(dire == 'W') st.dir = 3;
    if(dire == 'N') st.dir = 4;
    bfs();
    return 0;
}