[洛谷P3942] 将军令

洛谷题目链接:将军令

题目背景

 历史/落在/赢家/之手 
 至少/我们/拥有/传说 
 谁说/败者/无法/不朽 
 拳头/只能/让人/低头 
 念头/却能/让人/抬头 
 抬头/去看/去爱/去追 
 你心中的梦   

题目描述

又想起了四月。

如果不是省选，大家大概不会这么轻易地分道扬镳吧？ 只见一个又一个昔日的队友离开了机房。

凭君莫话封侯事，一将功成万骨枯。

梦里，小 F 成了一个给将军送密信的信使。

现在，有两封关乎国家生死的密信需要送到前线大将军帐下，路途凶险，时间紧迫。小 F 不因为自己的祸福而避趋之，勇敢地承担了这个任务。

不过，小 F 实在是太粗心了，他一不小心把两封密信中的一封给弄掉了。

小 F 偷偷打开了剩下的那封密信。他 发现一副十分详细的地图，以及几句批文——原来 这是战场周围的情报地图。他仔细看后发现，在这张地图上标记了 n 个从 1 到 n 标号的 驿站，n − 1 条长度为 1 里的小道，每条小道双向连接两个不同的驿站，并且驿站之间可以 通过小道两两可达。

小 F 仔细辨认着上面的批注，突然明白了丢失的信的内容了。原来，每个驿站都可以驻 扎一个小队，每个小队可以控制距离不超过 k 里的驿站。如果有驿站没被控制，就容易产 生危险——因此这种情况应该完全避免。而那封丢失的密信里，就装着朝廷数学重臣留下的 精妙的排布方案，也就是用了最少的小队来控制所有驿站。

小 F 知道，如果能计算出最优方案的话，也许他就能够将功赎过，免于死罪。他找到了 你，你能帮帮他吗？ 当然，小 F 在等待你的支援的过程中，也许已经从图上观察出了一些可能会比较有用的 性质，他会通过一种特殊的方式告诉你。

输入输出格式

输入格式：

从标准输入中读入数据。

输入第 1 行一个正整数 n,k,t，代表驿站数，一支小队能够控制的最远距离，以及特 殊性质所代表的编号。关于特殊性质请参照数据范围。

输入第 2 行至第 n 行，每行两个正整数 u_iui​ , v_ivi​ ，表示在 u_iui​ 和 v_ivi​ 间，有一条长度为 一里的小道。

输出格式：

输出到标准输出中。

输出一行，为最优方案下需要的小队数。

输入输出样例

输入样例#1：

4 1 0
1 2
1 3
1 4

输出样例#1：

1

输入样例#2：

6 1 0
1 2
1 3
1 4
4 5
4 6

输出样例#2：

2

说明

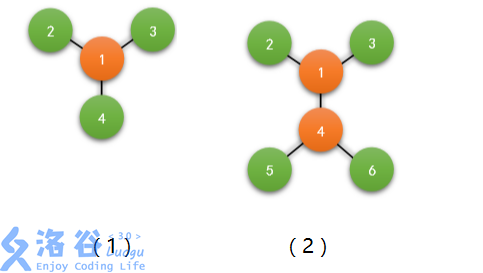
【样例 1 说明】

如图。由于一号节点到周围的点距离均是 1，因此可以控制所有驿站。

【样例 2 说明】

如图，和样例 1 类似。

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

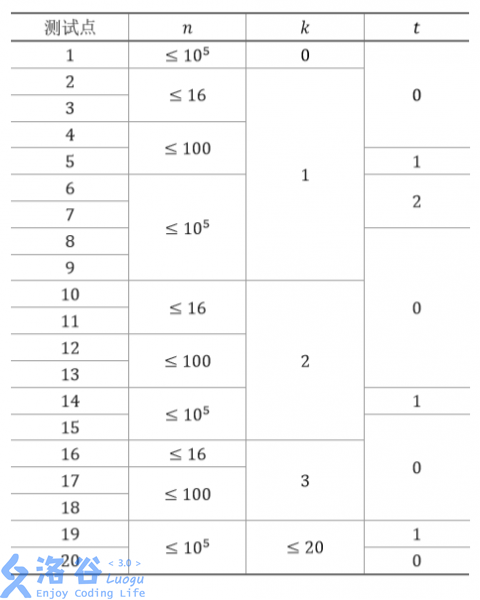
关于 t 的含义如下： t = 0：该测试点没有额外的特殊性质； t = 1：保证最多 8 个点的所连接的小道超过 1 条； t = 2：保证所有点到 1 号点的距离不超过 2。

每个测试点的数据规模及特点如下表

题面完






简述一下题意:给出一颗\(n\)个节点的树,以及控制一个节点后能同时覆盖的长度\(k\).现在要求出最少可以用多少节点覆盖整张图.






题目给出的是一颗树,可以直接将无根树转有根树,同时记录深度.

既然要覆盖整颗树,并且每个节点的深度都已经知道了.并且要覆盖一颗子树上的所有节点,只需要覆盖这颗子树的根节点.那么显然为了覆盖到深度为\(dep\)最深的节点,至少需要覆盖深度为\(dep-k\)的节点.

于是我们考虑一个贪心策略:

每次考虑深度最深且未被控制的节点\(x\).控制\(x\)上方深度为\(dep-k\)的节点.






但是有没有什么好办法能快速找到\(x\)上方深度为\(dep-k\)的节点呢?

我们可以直接从\(x\)开始扩展,扩展的距离为\(k*2\),那么这样得到的结果和从\(x\)上方深度为\(dep-k\)的节点开始扩展距离为\(k*2\)所得到的结果就是一样的了.

另外注意一下,如果直接对所有节点sort排序的话,数组的下标就会改变,要用结构体存下每个节点原来所代表的节点.

#include<bits/stdc++.h>
using namespace std;
const int N=100000+5;

int n, k, p, cnt = 0, last[N], ans = 0;
bool con[N], vis[N];

struct node{
    int dep, id;
}t[N];

struct edge{
    int to, nex;
}e[N*2];

int gi(){
    int ans = 0, f = 1; char i = getchar();
    while(i<'0'||i>'9'){if(i=='-')f=-1;i=getchar();}
    while(i>='0'&&i<='9'){ans=ans*10+i-'0';i=getchar();}
    return ans * f;
}

void add(int x,int y){
    e[++cnt].to = y;
    e[cnt].nex = last[x];
    last[x] = cnt;
}

bool cmp(node a,node b){
    return a.dep > b.dep;
}

void build(int x,int dep){
    vis[x] = 1; t[x].dep = dep;
    for(int i=last[x];i;i=e[i].nex){
	    int to = e[i].to;
	    if(!vis[to]) build(to,dep+1);
    }
}

void dfs(int x,int size){
    vis[x] = con[x] = 1;
    for(int i=last[x];i;i=e[i].nex){
	    int to = e[i].to;
	    if(!vis[to] && size > 0)
	        dfs(to , size-1);
	}
    vis[x] = 0;
}

int main(){
    int x, y; n = gi(); k = gi(); p = gi();
    for(int i=1;i<n;i++){
	    x = gi(); y = gi();
	    add(x,y); add(y,x);
    }
    for(int i=1;i<=n;i++) t[i].id = i;
    build(1,1); sort(t+1 , t+n+1 , cmp);
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=n;i++)
	    if(!con[t[i].id])
	        ans++, dfs(t[i].id,k*2);
	printf("%d\n",ans);
    return 0;
}