[洛谷P1856] [USACO5.5]矩形周长Picture

洛谷题目链接:[USACO5.5]矩形周长Picture

题目背景

墙上贴着许多形状相同的海报、照片。它们的边都是水平和垂直的。每个矩形图片可能部分或全部的覆盖了其他图片。所有矩形合并后的边长称为周长。

题目描述

编写一个程序计算周长。

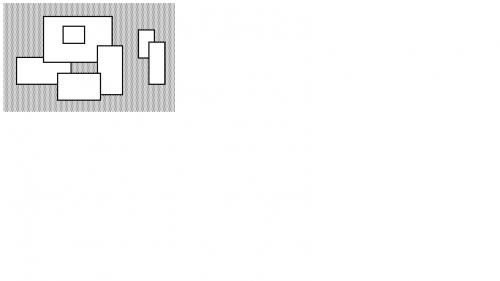
如图1所示7个矩形。

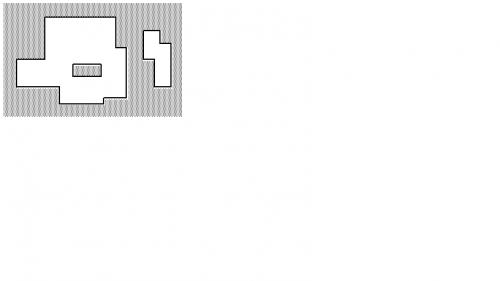
如图2所示，所有矩形的边界。所有矩形顶点的坐标都是整数。

输入输出格式

输入格式：

输入文件的第一行是一个整数N（0<=N<5000），表示有多少个矩形。接下来N行给出了每一个矩形左下角坐标和右上角坐标（所有坐标的数值范围都在-10000到10000之间）。

输出格式：

输出文件只有一个正整数，表示所有矩形的周长。

输入输出样例

输入样例#1：

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

输出样例#1：

228

题意: 给出一堆矩形,要你计算周长.

题解: 类似一堆矩形要你求某些信息的,基本上都可以用扫描线来做.

首先还是将矩形拆成线按照坐标排序,然后我们需要在线段树中记录几个变量:\(cov\)表示这个区间被覆盖的长度,\(sum\)表示这个区间的和(我们会在每次加入线段的时候给区间加上一个权值,会直接修改在\(sum\)变量里,但是\(sum\)标记不会下放).

接下来考虑如何写\(push\_up\)函数.首先判断一个节点被覆盖的长度先要看这个节点的\(sum\)是否有值,因为任何加入/删除线段的操作都会对\(sum\)进行修改,那么如果\(sum\)有值,显然\(cov=r-l+1\)(我这里使用的是闭区间).

如果\(sum\)的值为\(0\)呢?这时候我们需要判断这个节点是否为叶子节点,如果是叶子节点则\(cov=0\),否则\(cov=cov_{lson}+cov_{rson}\),判断是否为叶子的原因是防止越界.

然后查询的时候直接返回\(1\)节点的\(cov\)值就是整个区间内的覆盖数了.

那么答案如何统计呢?我这里是将\(x,y\)轴分两次求的,实际上可以一次做完,但是我自己\(yy\)的时候没想到这么多...

其实我们只需要每次插入一条线段,然后加入这次插入后\(cov\)的变化量的绝对值就可以了.

不懂可以看下代码.

#include<bits/stdc++.h>
#define ll(x) (x << 1)
#define rr(x) (x << 1 | 1)
using namespace std;
const int N = 10000+5;

int n, cnt[2], ans = 0;

struct line{ int x, l, r, v; }a[2][N*2];

bool cmp(line a, line b){ return a.x != b.x ? a.x < b.x : a.v > b.v; }

struct SegmentTree{ int l, r, sum, cov; }t[2][N*8];

void up(int x, int k){
    if(t[k][x].sum) t[k][x].cov = t[k][x].r-t[k][x].l+1;
    else if(t[k][x].l == t[k][x].r) t[k][x].cov = 0;
    else t[k][x].cov = t[k][ll(x)].cov+t[k][rr(x)].cov;
}

void build(int x, int l, int r, int k){
    t[k][x].l = l, t[k][x].r = r, t[k][x].sum = t[k][x].cov = 0;
    if(l == r) return; int mid = (l+r>>1);
    build(ll(x), l, mid, k), build(rr(x), mid+1, r, k);
}

void update(int x, int l, int r, int val, int k){
    if(l <= t[k][x].l && t[k][x].r <= r){
        t[k][x].sum += val, up(x, k); return;
    }
    int mid = (t[k][x].l+t[k][x].r>>1);
    if(l <= mid) update(ll(x), l, r, val, k);
    if(mid < r) update(rr(x), l, r, val, k); up(x, k);
}

void solve(int k){
    int last = 0, pos = 1; build(1, 1, N*2, k);
    sort(a[k]+1, a[k]+cnt[k]+1, cmp);
    for(pos = 1; pos <= cnt[k]; pos++){
        update(1, a[k][pos].l, a[k][pos].r-1, a[k][pos].v, k); //
        int add = abs(t[k][1].cov-last);
        ans += abs(t[k][1].cov-last), last = t[k][1].cov;
    }
}

int main(){
    ios::sync_with_stdio(false);
    int a1, b1, a2, b2; cin >> n;
    for(int i = 1; i <= n; i++){
        cin >> a1 >> b1 >> a2 >> b2;
        a1 += N, b1 += N, a2 += N, b2 += N;
        a[0][++cnt[0]] = (line){ a1, b1, b2, 1 };
        a[0][++cnt[0]] = (line){ a2, b1, b2, -1 };
        a[1][++cnt[1]] = (line){ b1, a1, a2, 1 };
        a[1][++cnt[1]] = (line){ b2, a1, a2, -1 };
    }
    solve(0), solve(1);
    cout << ans << endl;
    return 0;
}