[洛谷P4609] [FJOI2016]建筑师
洛谷题目链接:[FJOI2016]建筑师
题目描述
小 Z 是一个很有名的建筑师，有一天他接到了一个很奇怪的任务：在数轴上建 \(n\) 个建筑，每个建筑的高度是 \(1\) 到 \(n\) 之间的一个整数。
小 Z 有很严重的强迫症，他不喜欢有两个建筑的高度相同。另外小 Z 觉得如果从最左边（所有建筑都在右边）看能看到 \(A\) 个建筑，从最右边（所有建筑都在左边）看能看到 \(B\) 个建筑，这样的建筑群有着独特的美感。现在，小 Z 想知道满足上述所有条件的建筑方案有多少种？
如果建筑 \(i\) 的左(右)边没有任何建造比它高，则建筑 \(i\) 可以从左(右)边看到。两种方案不同，当且仅当存在某个建筑在两种方案下的高度不同。
输入输出格式
输入格式：
第一行一个整数 \(T\)，代表 \(T\) 组数据。 接下来 \(T\) 行，每行三个整数 \(n,A,B\)。
输出格式：
对于每组数据输出一行答案 \(\text{mod } 10^9+7\)。
输入输出样例
输入样例#1：
2
3 2 2
3 1 2
输出样例#1：
2
1
说明
对于 \(10 \%\) 的数据 ： \(1 \leq n \leq 10\)。
对于 \(20 \%\) 的数据 ： \(1 \leq n \leq 100\)。
对于 \(40 \%\) 的数据 ： \(1 \leq n \leq 50000, \ 1 \leq T \leq 5\)。
对于 \(100 \%\) 的数据 ：\(1 \leq n \leq 50000, \ 1 \leq A, B \leq 100, \ 1 \leq T \leq 200000\)。
题解:
首先来介绍一下斯特林数
这里只需要用到第一类斯特林数.
其实第一类斯特林数\(S(n, m)\)所代表的意义就是将\(n\)个数分成\(m\)个圆排列的方案数.我们知道\(S(n, m)=S(n-1, m-1)+(n-1)*S(n-1, m)\)可以这样理解,我们分两种情况讨论方案数,如果新加入一个数:
- 让它单独组成一个环,方案数为\(S(n-1,m-1)\).
- 将它放在之前\(n-1\)个数的左边,方案数为\((n-1)*S(n-1, m)\).
既然了解了斯特林数的含义,那么这里就可以拿来用了.
考虑找到最高的建筑,它一定会将左右两遍分成两个部分,且左边可以看见\(A-1\)个建筑,右边可以看见\(B-1\)个建筑.
那么除去我们挑出来的最高的建筑,还剩下\(n-1\)个建筑,我们需要将这\(n-1\)个建筑分成\(A+B-2\)个建筑群.一个建筑群指的是一栋可以被看见的建筑和在它后面被挡住的建筑.就像下面这张图红色框框内的建筑: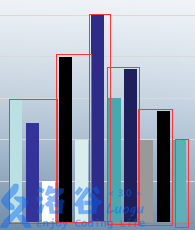
我们知道,建筑群需要让最高的建筑在最边上,这样才能保证这个建筑群内的建筑只有一座被看见,所以,一个建筑群内的排列相当于是一个圆排列(圆排列是经过旋转之后不相同的排列,也就是说圆排列中的任意一个排列都可以通过旋转来让最高的在最边缘).
然后产生了\(A+B-2\)个建筑群之后,我们需要选\(A-1\)个放在最高的建筑的左边,也就是\(C(A+B-2, A-1)\).
所以最后的答案就是\(C(A+B-2, A-1)*S(n-1, A+B-2)\),先预处理一下就可以\(O(1)\)回答了.
记得要开\(long\ long\)
#include<bits/stdc++.h>
using namespace std;
const int N = 5e4+5;
const int NN = 200+5;
const int mod = 1e9+7;
typedef int _int;
#define int long long
int T, n, a, b, C[NN][NN], S[N][NN];
_int main(){
cin >> T, C[0][0] = S[0][0] = 1;
for(int i = 1; i <= 200; i++) C[i][i] = C[i][0] = 1;
for(int i = 1; i <= 200; i++)
for(int j = 1; j <= i; j++) C[i][j] = (C[i-1][j]+C[i-1][j-1])%mod;
for(int i = 1; i <= 50000; i++)
for(int j = 1; j <= 200; j++) S[i][j] = (S[i-1][j-1]+(i-1)*S[i-1][j]%mod)%mod;
while(T--){
cin >> n >> a >> b;
cout << C[a+b-2][a-1]*S[n-1][a+b-2]%mod << endl;
}
return 0;
}
