BUAA SE 个人项目作业

项目 | 内容

• | -
  这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
  这个作业的要求在哪里 | 个人项目作业 |
  我在这个课程的目标是 | 通过个人项目实践熟悉个人开发流程 |

一、在文章开头给出教学班级和可克隆的 Github 项目地址

• 教学班级：005
• 项目地址：https://github.com/NoSameRain/BUAA_SE_IntersectPrj

二、在开始实现程序之前，在下述 PSP 表格记录下你估计将在程序的各个模块的开发上耗费的时间。

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	60	90
· Design Spec	· 生成设计文档	30	30
· Design Review	· 设计复审 (和同事审核设计文档)	15	10
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10	10
· Design	· 具体设计	90	120
· Coding	· 具体编码	100	120
· Code Review	· 代码复审	60	60
· Test	· 测试（自我测试，修改代码，提交修改）	120	170
Reporting	报告
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	30	30
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60	80
	合计	615	760

三、解题思路描述。即刚开始拿到题目后，如何思考，如何找资料的过程。

1. 题目要求

给定 N 条直线，询问平面中有多少个点在至少 2 条给定的直线上。题目输入保证答案只有有限个。

输入格式

• 第 1 行：一个自然数 N >= 1，表示输入的直线的数目。注：具体的 N 的限制参见评分规则。
• 第 2 行至第 N + 1 行：每行描述一条直线。具体格式如下：
  • 直线：L ，表示通过点 (x1, y1) 和 (x2, y2) 的直线。输入保证给定两点不重合。

所有直线参数均为整数，范围为 (-100000, 100000)。

输出格式

共 1 行，输出平面中满足需求的点的数目。

2. 解题思路

对于任意两条直线，位置关系有两种情况：相交、平行（重合），即交点个数可能为：1个、0个。

在最初看到题目时，我的思路是将任意两条直线的交点求出并保存，最后记录交点个数。对于N=1的情况直接判定交点个数为0。对于N>1的情况，先判断两条直线是否平行，若平行则转而对其他直线进行判断，否则求出这两条直线的交点坐标，确定这个交点坐标之前没有出现过后再保存它。

这次题目我在保存直线的什么信息上思考了稍久，主要还是根据要利用什么方法求交点坐标来决定。这次我利用了“已知两条直线四个点的坐标，根据四个坐标值直接求交点坐标”的方法，可参见下面这个博客。

两点确定一条直线，已知四个点确定的两条直线，求这两条直线的交点

求坐标方法和具体公式确定了，相应的数据结构也就能确定了。由于这个公式中用到的数据只涉及坐标值，所以我在直线的类中就存储了这个直线的x1 y1 x2 y2的值，以及斜率k值，以方便之后判断两条直线的位置关系（平行、相交）。

由于一个假期没写代码有些生疏，所以复习c++的vector、map容器等知识也花费了一部分时间。

四、设计实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？单元测试是怎么设计的？

我的代码只设置了line类用于存储直线的相关信息。函数只有4个。分别用来对输入值进行处理、存储直线信息、判断所有直线中任意两条直线的位置关系、计算交点坐标并进行存储。我这次代码写的比较面向过程，基本在main函数里一个个调用了其余几个有特定功能的函数。由于结构和函数功能都比较简单所以不需要流程图。单元由于这次要实现的功能不是特别复杂所以单元测试颗粒粒度较大。基本是针对整个大功能进行测试（即直接测试最后输出的交点个数是否正确）没有对其中几个小功能进行测试。测试样例都是根据一些边界条件以及直线位置关系来设计的。比如输入的坐标值设为-9999、9999等这样的值，以及令所有直线都平行、部分平行部分相交、所有直线都交于同一点、部分直线交于同一点部分直线不交于同一点等情况的组合。由于分析覆盖率的插件一直无法下载所以未分析覆盖率。

五、记录在改进程序性能上所花费的时间，描述你改进的思路，并展示一张性能分析图（由 VS 2019 的性能分析工具自动生成），并展示你程序中消耗最大的函数。

改进性能起码花费了3个小时。主要涉及给交点去重的部分。最开始我是将计算出的交点坐标存储在一个二维数组中，每次存储之前先通过遍历数组查找这一交点是否与数组中的交点重复。但这个方法由于性能太差直接被我pass掉了（后来反思应该是遍历这里做的不够好，导致N大于1000时直接爆掉）

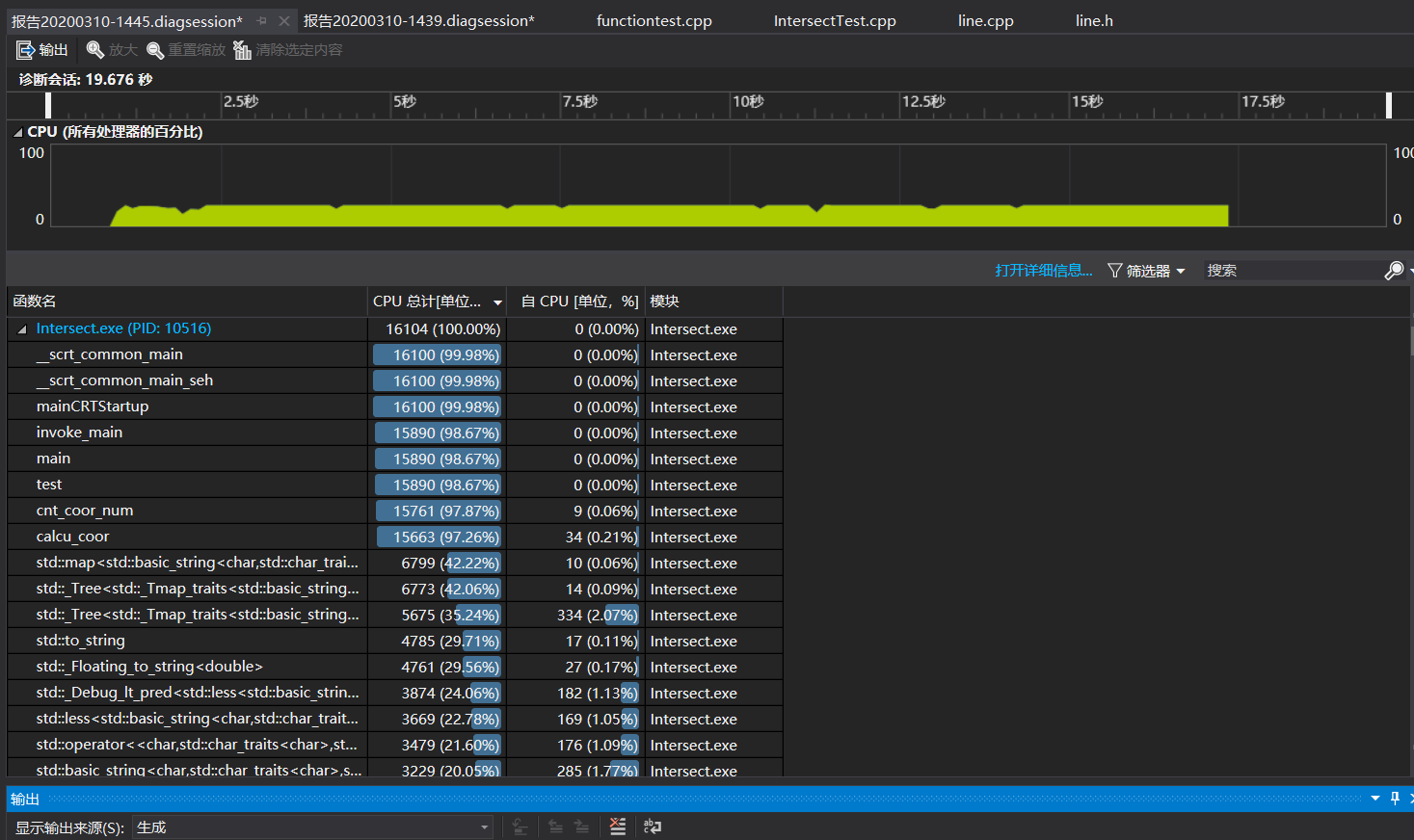
后来想到map键值的唯一性，就想利用这个特性来代替遍历去重的工作，于是改用map来存储所有交点坐标。实施后性能改善了很多。但可以看出map所带来的消耗还是很大的。以及我在这里为了将x、y坐标作为键值存储用了一个很奇怪，或者说不太符合规范？的方法。我将x、y全都转换为string类型并连接了起来。这里可以看到to_string也带来了相当大的消耗。但这里我还是不能很好解决。导致其所在的函数消耗也很大。（这里写了一个用于测试性能的代码，主要是随机生成1000个x、y坐标值在-10000到10000之间的字符串。）

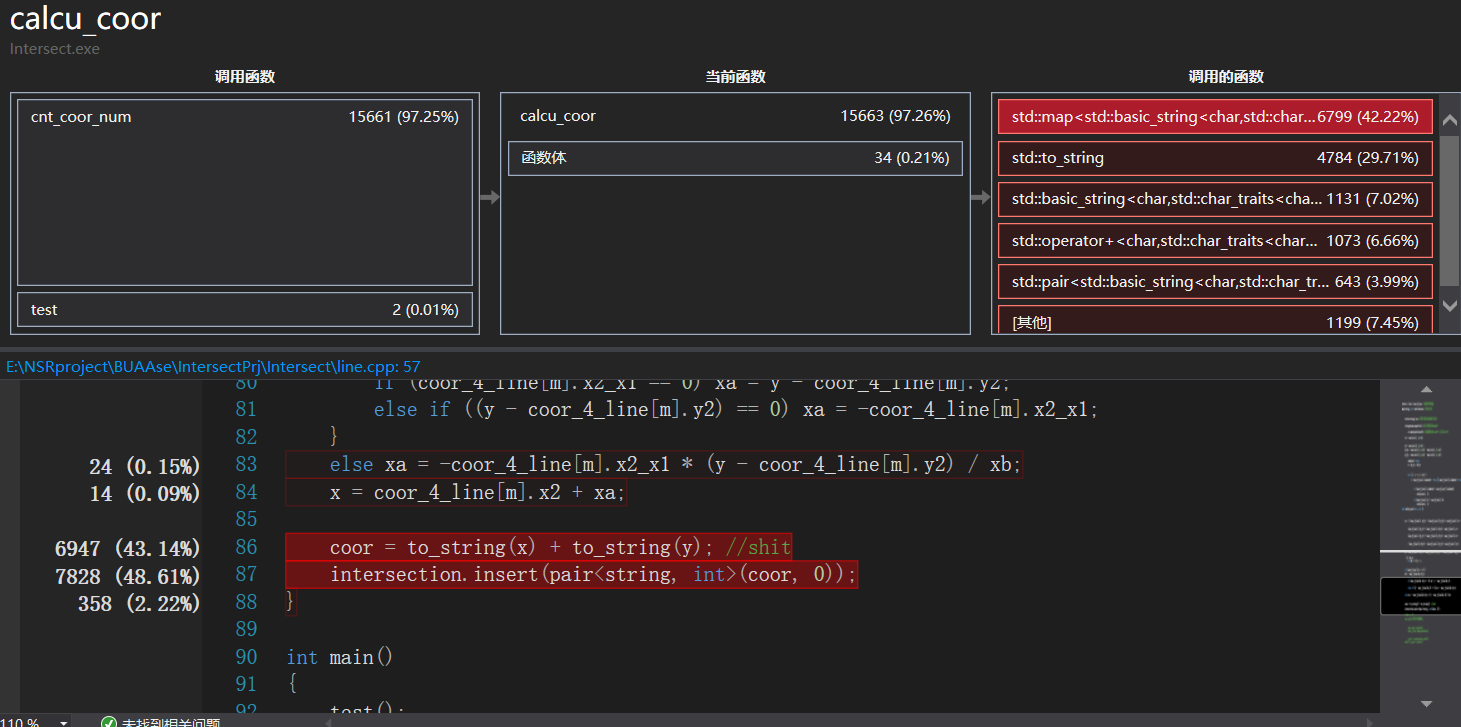
以及这里再补充一下code quality analysis情况，刚开始涉及一些变量未赋初始值的问题，后来都改掉了

六、代码说明。展示出项目关键代码，并解释思路与注释说明。

1.类说明

class line
{
public:
	int x1 = 0;
	int x2 = 0;
	int y1 = 0;
	int y2 = 0;
	int x2_x1 = 0; //x2 - x1
	int y2_y1 = 0; //y2 - y1
	double k = 0;
	bool ulimited = false; //无斜率;

	void store_coor(string str);
};

可以看出这一部分主要就是对直线坐标和斜率进行存储，以方便之后的计算。

2. 函数说明

这个函数用来处理字符串并给相应的对象赋值

void line::store_coor(string str)
{	
	vector<string> res;//用于存放分割后的字符串 
	string result;//暂存从str中读取的字符串 
	stringstream input(str);//将字符串读到input中 
	while (input >> result)
		res.push_back(result);//依次输出到result中，并存入res中 

	x1 = stoi(res[1], 0, 10);
	y1 = stoi(res[2], 0, 10);
	x2 = stoi(res[3], 0, 10);
	y2 = stoi(res[4], 0, 10);;
	x2_x1 = stoi(res[3], 0, 10) - stoi(res[1], 0, 10);
	y2_y1 = stoi(res[4], 0, 10) - stoi(res[2], 0, 10);
	if (x2_x1 == 0)
	{
		ulimited = true;
	}
	else
	{
		k = y2_y1 / x2_x1;
	}
}

这一部分用来遍历所有的直线，判断其中两条直线的位置关系并计算交点坐标

void cnt_coor_num()
{
	int i, j;
	for (i = 0;i < N;i++)
		for (j = i + 1;j < N;j++)
		{
			if (coor_4_line[i].ulimited == true || coor_4_line[j].ulimited == true)
			{
				if (coor_4_line[i].ulimited != coor_4_line[j].ulimited)
				{
					calcu_coor(i, j);
				}
			}
			else
			{
				if (coor_4_line[i].k != coor_4_line[j].k)
				{
					calcu_coor(i, j);
				}
			}
		}
}

这一部分用来计算两条直线的交点坐标。bug也主要是出现在这里。因为用坐标来直接计算有时候会涉及分子分母为0的情况，这一点我在最开始没有好好思考就急着写代码了，后来决定将分子分母为0的情况单列出来讨论（有时候涉及到分子分母同时消去0）这可能是直接用坐标值计算交点坐标这种方法的一个缺点。

现在再看真的是有点不堪入目。。。。虽然功能实现了，但是不够简洁优美

void calcu_coor(int i, int j)
{
	string coor;
	double x, y, xa;
	int ya,yb,xb;
	xa = 0;
	ya = ((-coor_4_line[i].y2_y1) * (coor_4_line[j].y2_y1) * coor_4_line[i].x1 +
		(coor_4_line[j].y2_y1) * (coor_4_line[i].x2_x1) * coor_4_line[i].y1 +
		(coor_4_line[i].y2_y1) * (coor_4_line[j].y2_y1) * coor_4_line[j].x1 +
		(-coor_4_line[j].x2_x1) * (coor_4_line[i].y2_y1) * coor_4_line[j].y1);
	yb = coor_4_line[i].x2_x1 * coor_4_line[j].y2_y1 + (-coor_4_line[i].y2_y1) * coor_4_line[j].x2_x1;
	if (ya == 0)
	{
		if (yb == 0) y = 1;
		else y = 0;
	}
	else y = ya / yb;
	int m = j;
	if (coor_4_line[j].k == 0) {
		m = i;
	}
	xb = -coor_4_line[m].y2_y1;
	if (xb == 0)
	{
		if (coor_4_line[m].x2_x1 == 0) xa = y - coor_4_line[m].y2;
		else if ((y - coor_4_line[m].y2) == 0) xa = -coor_4_line[m].x2_x1;
	}
	else xa = -coor_4_line[m].x2_x1 * (y - coor_4_line[m].y2) / xb;
	x = coor_4_line[m].x2 + xa;

	coor = to_string(x) + to_string(y); //shit
	intersection.insert(pair<string, int>(coor, 0));
	//duplicate_remove(x, y);
}

七、在你实现完程序之后，在下述 PSP 表格记录下你在程序的各个模块上实际花费的时间。

见上面的表格。可以看到实际花费的时间还是比预期多很多。主要是后面进行单元测试、改进性能、修改代码花费了很多时间。