堆排序复习
堆排序复习
摘要：本文时对堆排序进行的简单复习，因为已经基本上了解了堆排序的底层原理，因此本篇笔记更注重对堆排序代码的书写，本篇笔记将把堆排序分成两个部分：堆调整部分和堆排序部分。
1.堆调整部分
堆调整部分时整个堆排序中最为重要且复杂的部分，该部分的功能简单且抽象：将一棵只有根节点导致整棵树不是堆的树重新调整成堆。是的这个核心部分的功能就是这么简单且鸡肋，至少看上去相当鸡肋。其功能有点像通过一个外来节点将两个堆合并成一棵树之后，再通过某种手段将其恢复成堆，此时仅有根节点的存在可能导致整棵树不是堆，而根节点的两棵子树都是堆。这个算法并不能直接构建出一个堆，其功能只是一个非常简单的堆的调整。
那么问题来了，我们如何使用这样简陋的一个方法生成一个我们心目中的堆呢？要知道树的结构是具备递归性的，要怎么理解呢？再二叉树中，一棵树可以被分为根节点和两棵子树，而一棵子树又可以按照这个规则被重复的划分，我们只要重复的这样划分，就可以将该树划分成一个最小的单位，也就是双层树，这个名词是我编的，但是这是堆排序中的最小问题处理单位，如图所示：
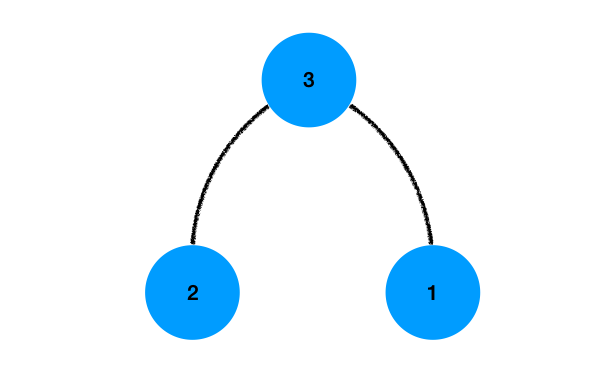
双层树的特点是它的两棵子树就是叶子节点，而一个节点一定是一个堆，因此在双层树中我们一定可以保证一个根节点的两棵子树是堆，因此我们可以直接使用这个算法。
这个算法的思路就是：获取到树的根节点，然后将根节点下放(如果根节点合理的话那就不下放)到一个合理的位置，保持这棵树仍然是一个堆，然后我们将这棵树从后到前的遍历，并且执行这个算法，这样一来我们就可以保证后边这棵树从基础起，每一棵子树都是堆，进而往前推，最终整棵树都变成了一个堆。
现在让我们来看看这个算法：
public static void heapAdjest(int[] arr,int parent,int length){
int temp = arr[parent];//获取到根节点的值
int child = parent * 2 + 1;//根据根节点获取到孩子节点的位置
while (child<length){//只要孩子节点小于整个数组的长度，我们便保持循环
if(child+1<length&&arr[child+1]>arr[child]){//如果孩子节点的下一个位置还有数值
//说明当前树是有右孩子节点存在的
child++;//通过比较如果发现右孩子节点更大的话，那我们就使用右孩子节点进行之后的对比
}
if(temp>=arr[child]){//如果我们发现根节点的值大于更大的那个孩子节点，那么我们就直接退出
break;
}
arr[parent] = arr[child];//否则我们进行一次交换，我们直接将孩子节点的值赋值给根节点
parent = child;//然后我们让parent的位置直接等于child，这里相当于交换，因为我们已经保存了parent的值了
//实际上这里就是我们上面所说的根节点下放
child = parent * 2 + 1;//之后我们让孩子节点也跟随根节点进行更新，以便进入下一轮循环
}
arr[parent] = temp;//我们最终将temp的值放在当前的parent指针上
}
2.堆排序部分
在堆排序部分我们的思路变得更加简单，我们首先使用上面的堆调整算法从后往前的构建出一个堆来，然后我们就能保证整棵树的根节点一定是整个数组中最大的元素了，我们让根节点和数组中的最后一个元素交换，这样一来就能保证当前树中最大的元素被排列到了数组的最后边，然后我们缩小树的规模；由于规模更改之后的树结构发生了变化，其根节点的数值变了，但是其左右子树仍然绝对是一个堆，而去掉数组中最后一个元素的行为实际上相当于从堆的最左叶子节点上摘取了一个，这个行为不会影响一棵树是否还是堆，因为这个行为是删除最小的，而非修改最大的，堆中的大小逻辑并没有被破坏，因此我们可以保证两个子树仍然是堆，而我们再调整一次新的堆即可。我们重复这个行为直到堆中所有的元素都被摘走，这个数组也宣告排序完成。
代码：
public static void heapSort(int[] arr){
for(int i = arr.length - 1;i>=0;i--){
heapAdjest(arr,i,arr.length);
}
for(int i = arr.length-1;i>=0;i--){
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapAdjest(arr,0,i);
}
}
3.堆排序图示
1.调整阶段
2.排序阶段
4.代码
public static void heapSort(int[] arr){
for(int i = arr.length - 1;i>=0;i--){
heapAdjest(arr,i,arr.length);
}
for(int i = arr.length-1;i>=0;i--){
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
heapAdjest(arr,0,i);
}
}
public static void heapAdjest(int[] arr,int parent,int length){
int temp = arr[parent];
int child = parent * 2 + 1;
while (child<length){
if(child+1<length&&arr[child+1]>arr[child]){
child++;
}
if(temp>=arr[child]){
break;
}
arr[parent] = arr[child];
parent = child;
child = parent * 2 + 1;
}
arr[parent] = temp;
}
5.运行测试
