1073. 负二进制数相加
1073. 负二进制数相加
给出基数为 -2 的两个数 arr1 和 arr2，返回两数相加的结果。
数字以 数组形式 给出：数组由若干 0 和 1 组成，按最高有效位到最低有效位的顺序排列。例如，arr = [1,1,0,1] 表示数字 (-2)^3 + (-2)^2 + (-2)^0 = -3。数组形式 中的数字 arr 也同样不含前导零：即 arr == [0] 或 arr[0] == 1。
返回相同表示形式的 arr1 和 arr2 相加的结果。两数的表示形式为：不含前导零、由若干 0 和 1 组成的数组。
示例 1：
输入：arr1 = [1,1,1,1,1], arr2 = [1,0,1]
输出：[1,0,0,0,0]
解释：arr1 表示 11，arr2 表示 5，输出表示 16 。
示例 2：
输入：arr1 = [0], arr2 = [0]
输出：[0]
示例 3：
输入：arr1 = [0], arr2 = [1]
输出：[1]
提示：
1 <= arr1.length, arr2.length <= 1000arr1[i]和arr2[i]都是0或1arr1和arr2都没有前导0
我的解题：
这道题属于一个数学思想问题，主要难点在于理解负二进制数的计数法概念，而不是写代码，只要理解了这个概念代码的思路很容易就能够想出来。现在让我们来研究这道题的题干：基数为-2的两个数arr1和arr2，什么是基数呢？基数是一个很基础的数学概念，这个概念由于过于基础而属于底层数学研究的范畴因为不包含在九年义务教育之内，可能只要大学的数学专业才会研究到这个概念，以上纯属猜测，反正我是没学过这个概念。基数概念我们可以简要理解为逢n进1的那个n，如十进制数是逢十进一，那么基数就是10，2进制是逢2进一，那么基数就是2，而从更基础底层的概念来理解基数属于一个集合论思想，基数乃一个集合的范围，比如十进制的每个位上的数字都是0~9这十个数字，二进制的每个位上都是0~1这两个数字，基数就是集合的大小，在这里我们简单的理解为逢基数进1就行了，那么负二进制数就是逢负二进一，这个着实难以理解，实际上上边说的知识对于负二进制数可能都是废话，使用进一思想其实很难理解负二进制数。
好在我们还有另一个思路来理解负二进制数，那就是拆数的思路，我们把一个十进制数1234可以拆成：\(1*10^3+2*10^2+3*10^1+4*10^0\)，同理我们可以将二进制数100110拆成：\(1*2^5+0*2^4+0*2^3+1*2^2+1*2^1+0*2^0\)，而对于负二进制数的11111我们可以拆成：\(1*(-2)^4+1*(-2)^3+1*(-2)^2+1*(-2)^1+1*(-2)^0\) = 1-2+4-8+16 = 11，正好和题目中的数值对应，说明负二进制数的计算就是这样算的，同时这里的算式中的底数部分，就是基数，如10，2以及此处的-2，就是我们上面所说的基数，而现在我们了解了负二进制数的计算方式，我们如何理解负二进制数的相加呢？
这里实际上涉及了一部分简单的中国传统哲学，即二元论，阴阳的对应以及阴阳的相互转化，二进制数和负二进制数的区别在于二进制数的每个位上边的数字都是正的，因此通过拆数的方式进行计算之后直接相加即可得到十进制的结果，而负二进制数的每个位数上出现了符号的区别，其奇数位的符号是正数，偶数位上的符号是负数，这不仅仅标明我们在计算其加和的时候需要引入符号，还意味着其奇数位和偶数位存在了正负之相对的情况，其奇数位上的数字和偶数位上的数字不仅仅有数值大小这个概念，还出现了正负之性质，而这个正负之性质实际上是可以转化的，一个数字是正还是负，其实不取决于它是奇数位还是偶数位，而是取决于我们的出发视角，如果我们以其中的第n位出发，并认为其是正的，那么它相邻的两位必定都是负的，也就是说我们在负二进制数中位数之间两两为负，两两相反，简而言之，相邻位上的进位是负的，我们再具体一些，我们以11111+101为例：
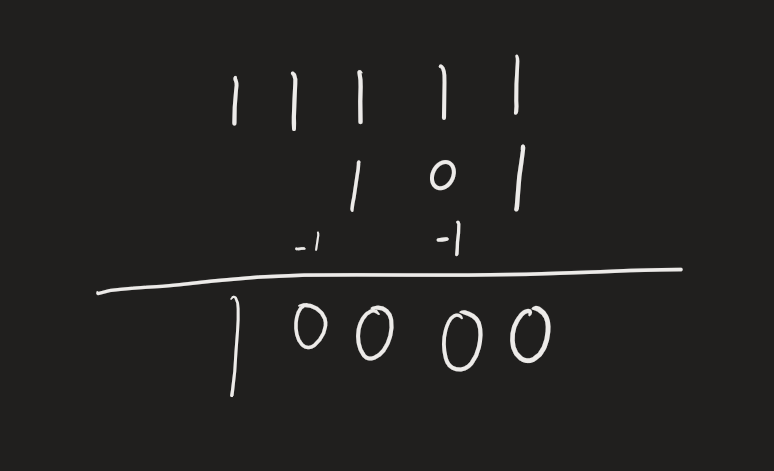
可见结果完全正确，这实际上就是因为在负二进制数中，数位之间两两为负，低位相当于高位来说永远是负数，而低位的进位贡献，相当于高位来说自然是一个负贡献，因此向高位的进位就是减1，我们现在再来研究一下借位概念：
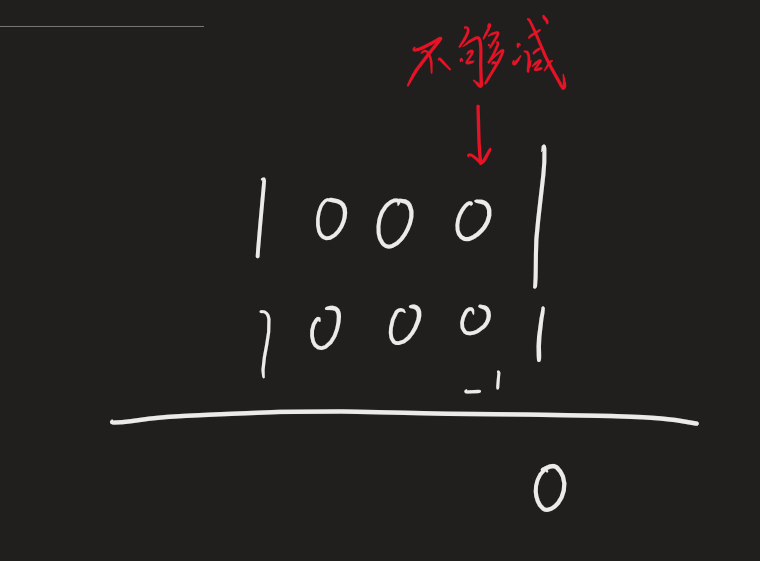
这里出现了不够减的现象，因此需要向高位借位，需要注意的是，借位的行为，在普通进制运算时本是一个负贡献，但是这里的低位相对高位来讲是负的，因此高位要是想要给低位进行一个正贡献，那么需要献给低位一个和低位相同性质的数，而这个数和低位性质相同，和自身自然性质相反，也就是说，这个数字的付出，是付出了一个和自身相反的数字，而负负得正，失去一个和自身相反的数字相当于得到了一个和自身性质相同的数字，也就是说向低位借位，实际上对自己做了一个正贡献，在二进制数中，向低位借位，会导致自身减1，低位加2，而在负二进制数中这个情况变得相当离奇，向低位借位，会让低位获得2，自己也获得1，如下：
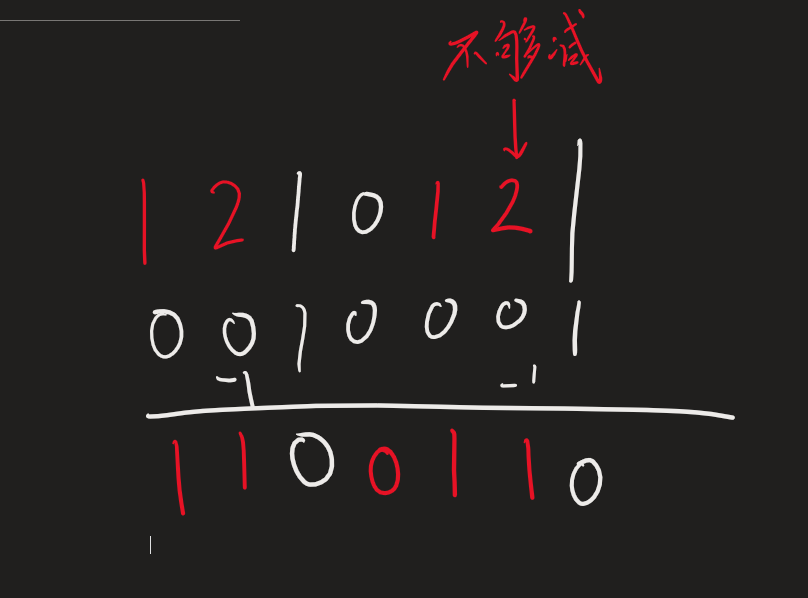
在数字的计算当中，进位和借位就是加和计算的全部了，因此根据上面这些数学原理，我们就可以进行负二进制数的相加算法设计了。对于该问题的算法设计，我们可以根据这个计数原理设计成这样的：对于两个数组先直接相加，结果保留在较长的那个数组中，如果两个数组等长那么保存在任一个数组中，然后我们遍历这个保存结果的数组，如果某一位n是2或者2以上的数字，我们便将其置为(n-2)，而往高位进一位，这个进位是-1，如果够减那么就直接减1，否则向更高位借位，并向那个更高位加1位，这种运算最终可能会在最高位发生一个进位，我们根据这个进位的具体情况进行数组的扩容，如果是一个-1，那么我们需要扩容两位，并先补零，然后按照借位法则进行运算，除了这种进位情况，无其他的进位情况了，这个和我们的负二进制数的性质有关，然后我们返回这个数组即可。我们以11111+101为例示范：
1 1 1 1 1
+ 1 0 1
—————————————
1 1 2 1 2
第一步： 1 1 2 1 2
第二步： 1 1 2 0 0
第三布： 1 0 0 0 0
对于有借位的情况我们这样计算，如1001+1001：
1 0 0 1
+1 0 0 1
---------
2 0 0 2
第一步：2002
第二步：2110
第三步：002110
第四步：110110
只有结果的第一位是2以及2以上的数字是才会向高位产生借位，此时我们就需要扩容两位，根据规律我们发现直接将这两位赋值为11就行了。因此我们可以书写算法如下：
class Solution {
public int[] addNegabinary(int[] arr1, int[] arr2) {
// 定义规则：0+1=1，进位向前边减一，够减则减，不够减则借位
int[] outCome = null;
if (arr1.length > arr2.length) {
for (int i = 1; i <= arr2.length; i++) {
arr1[arr1.length - i] += arr2[arr2.length - i];
}
outCome = arr1;
} else {
for (int i = 1; i <= arr1.length; i++) {
arr2[arr2.length - i] += arr1[arr1.length - i];
}
outCome = arr2;
}
// System.out.println(Arrays.toString(outCome));
int add = 0;
for (int i = outCome.length - 1; i > 0; i--) {
if (outCome[i] + add >= 2) {
add = -1;
outCome[i] -= 2;
} else if (outCome[i] + add < 0) {
outCome[i - 1] += 1;
outCome[i] = 1;
add = 0;
} else {
outCome[i] += add;
add = 0;
}
}
outCome[0] += add;
//System.out.println(Arrays.toString(outCome));
if (outCome[0] >= 2) {
outCome[0] -= 2;
int[] newOutCome = new int[outCome.length + 2];
newOutCome[0] = 1;
newOutCome[1] = 1;
for (int i = 0; i < outCome.length; i++) {
newOutCome[2 + i] = outCome[i];
}
outCome = newOutCome;
}
// System.out.println(Arrays.toString(outCome));
if (outCome[0] == 0) {
int zlength = 0;
while (zlength < outCome.length && outCome[zlength] == 0) {
zlength++;
}
System.out.println(zlength);
if (zlength == outCome.length) {
outCome = new int[1];
outCome[0] = 0;
} else {
int[] newOutCome = new int[outCome.length - zlength];
for (int i = 0; i < newOutCome.length; i++) {
newOutCome[i] = outCome[zlength + i];
}
outCome = newOutCome;
}
}
return outCome;
}
}
