二叉排序树节点删除详解
二叉排序树节点删除详解
摘要：本篇笔记作为补充笔记，主要讲解在二叉排序树中的节点删除这一行为的操作。
1.为何要重点探究二叉排序树中的节点删除？
二叉排序树不是普通的树，在二叉排序树中节点之间是有序的，因此在二叉排序树中直接对节点进行修改是不被允许的，如果我们能够恣意修改二叉排序树中的值，那这棵树很可能会乱套，因此我们必须规范在二叉排序树中的修改行为，我们通常在二叉排序树中不设置修改的方法，而是设置一个按值查找并删除的方法，接下来我们就重点介绍一下二叉排序树中的删除方法。
2.二叉排序树中的几种节点的删除
2.1.叶子节点的删除
如果删除的目标是一个叶子节点，那么事情就简单了，因为叶子节点没有子树，所以叶子节点的删除就是简单的删除，把它删了，完全不会影响到整棵树的平衡性，因此理论上将叶子节点的删除最为简单，那么接下来让我们理一下叶子节点的删除步骤：
1.找到要删除的节点，我们将其命名为targeNode
2.找到要删除的节点的父节点，我们命名为parent
3.判断targeNode节点是parent节点的左子节点还是右子节点
4.根据第三步的结果将其parent的左孩子或者右孩子置为null，从而删除目标节点，若是左子节点：parent.left = null;若是右子节点：parent.reight = null
2.2.非叶子节点的删除(只有一个孩子节点)
只有一个孩子节点的非叶子节点的删除，需要考虑的问题就多了一些，我们需要考虑到将这个目标节点删除之后，其孩子节点何去何从，我们不能像处理叶子节点一样直接将其父节点的某个孩子节点置空了，而是需要让它的孩子节点接在父节点上，如图所示：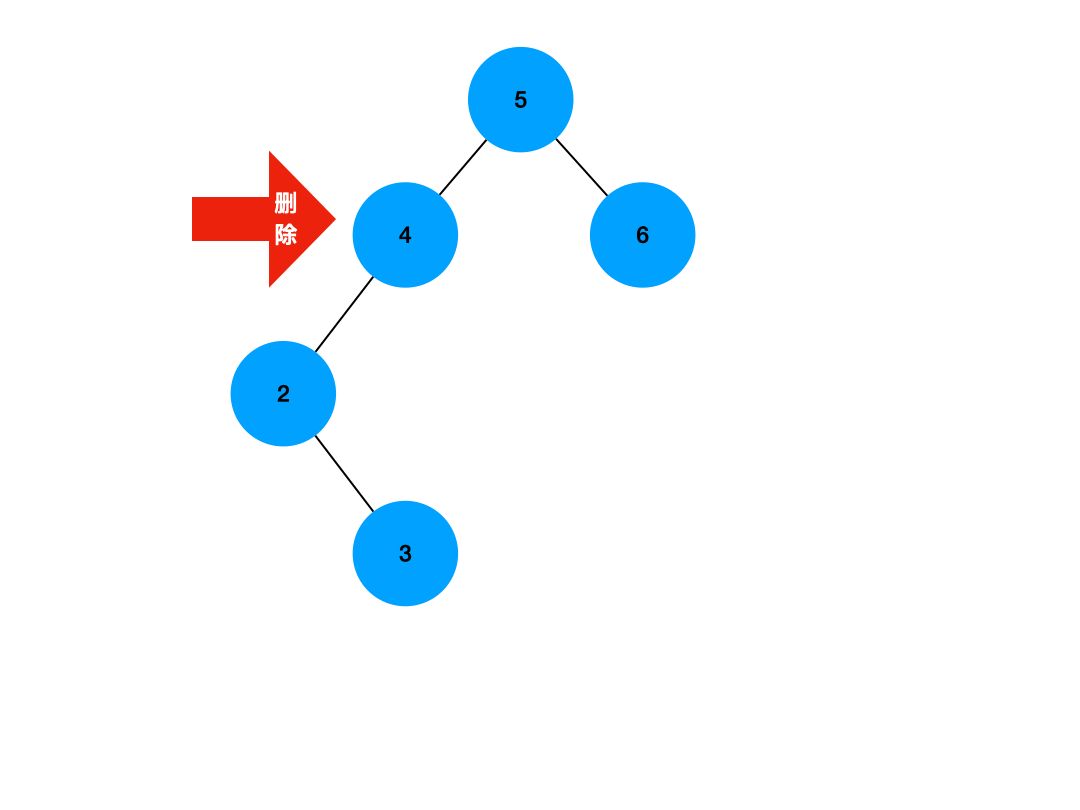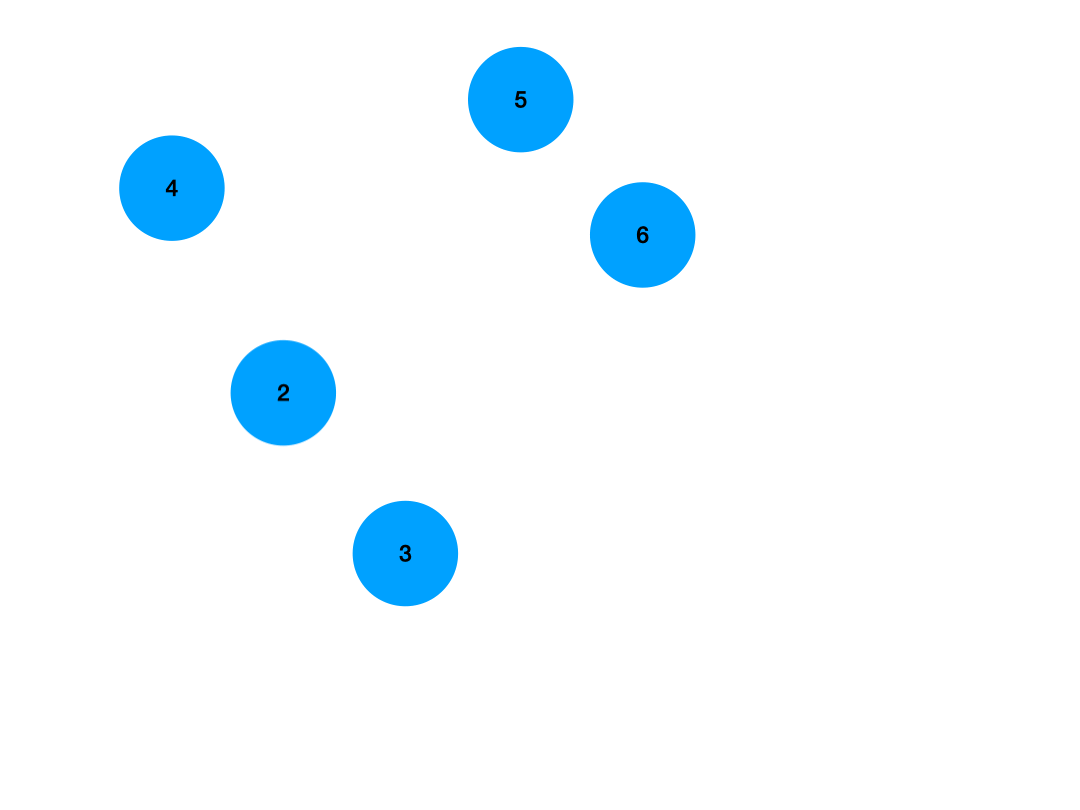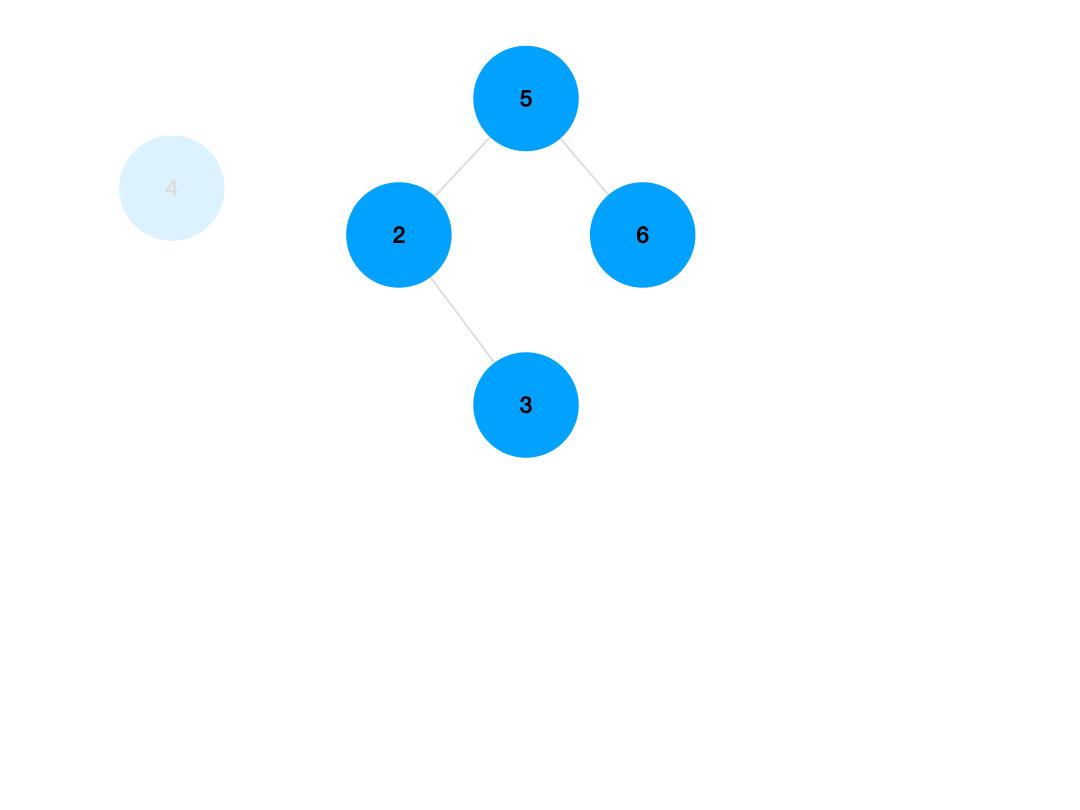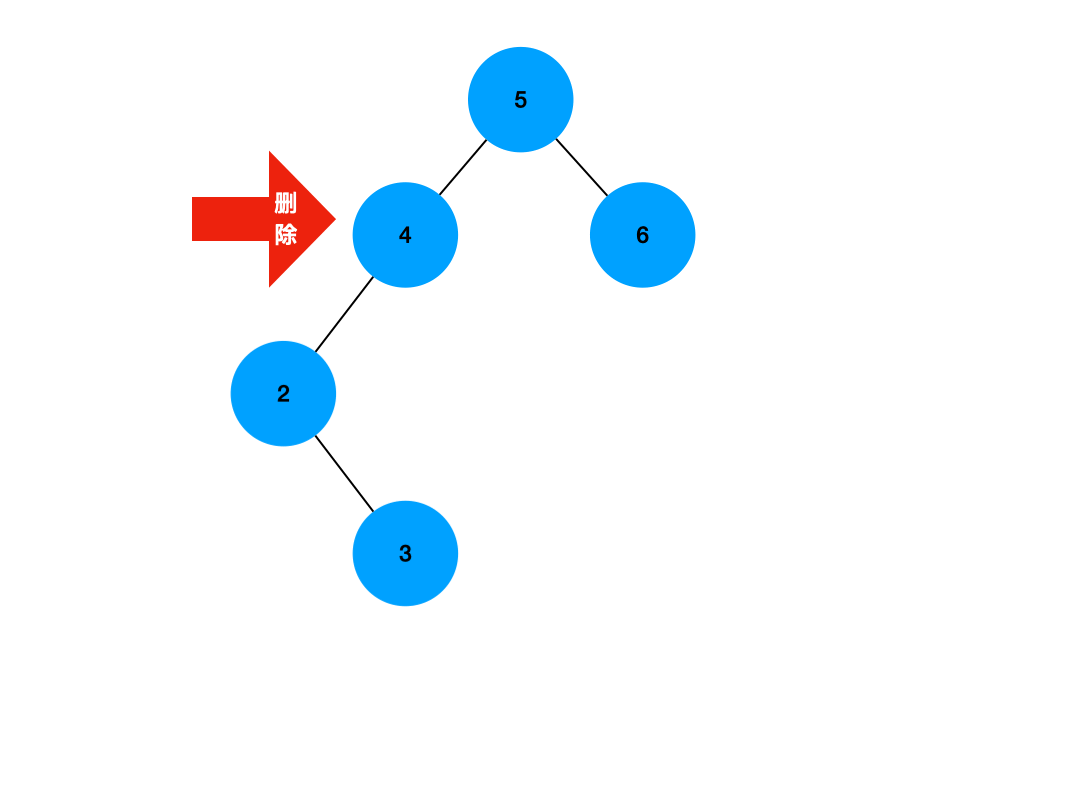
我们需要先获取到将要被删除的节点所拥有的那棵子树的根节点，如上图所示，我们需要获得其左子树的根节点，之后，由于将要被删除的节点是其父节点的左子树，因此以它为根节点的这棵子树，一定是全都小于它父节点的，因此这个将要被删除的节点的子树，也一定是要被接在其父节点的左边的，如果不像上图那样，这个将要被删除的节点位于其父节点的右侧，则说明其所在子树的所有值都大于父节点，那么我们就将其唯一的那个子树根节点接在父节点的右侧，这个逻辑过程仍然不难理解，接下来我们写出步骤：
1.找到要删除的节点，我们命名为targeNode
2.找到删除节点的父节点，我们命名为parent
3.找到要删除节点的唯一子树的根节点，这个节点可能是将被删除的节点的左孩子节点或者右孩子节点，但由于它是唯一的，所以我们找到之后直接命名为child
4.判断targeNode是其父节点parent的左子节点还是右子节点，如果是左子节点：parent.left = target.child; 如果是右子节点：parent.right = target.child
2.3.非叶子节点的删除(有两个孩子节点)
这个情况看上去比较复杂，实际上操作起来并不困难，使用下面的方法，甚至都不用删除指定节点，只需按照规则修改其中的值即可：
1.找到将被删除节点的左子树中的最大值
2.将这个最大值保存，并删除这个节点
3.将我们保存到的左子树最大值替换给将被删除的节点的值
或者我们可以使用右子树：
1.找到将被删除节点的右子树中的最小值
2.将这个最小值保存，并删除这个节点
3.将我们保存的右子树的最小值替换给将被删除节点的值
这两个方法思路一样，只不过是方向不同，如下图，我们使用更直观的图片来展示这个过程：
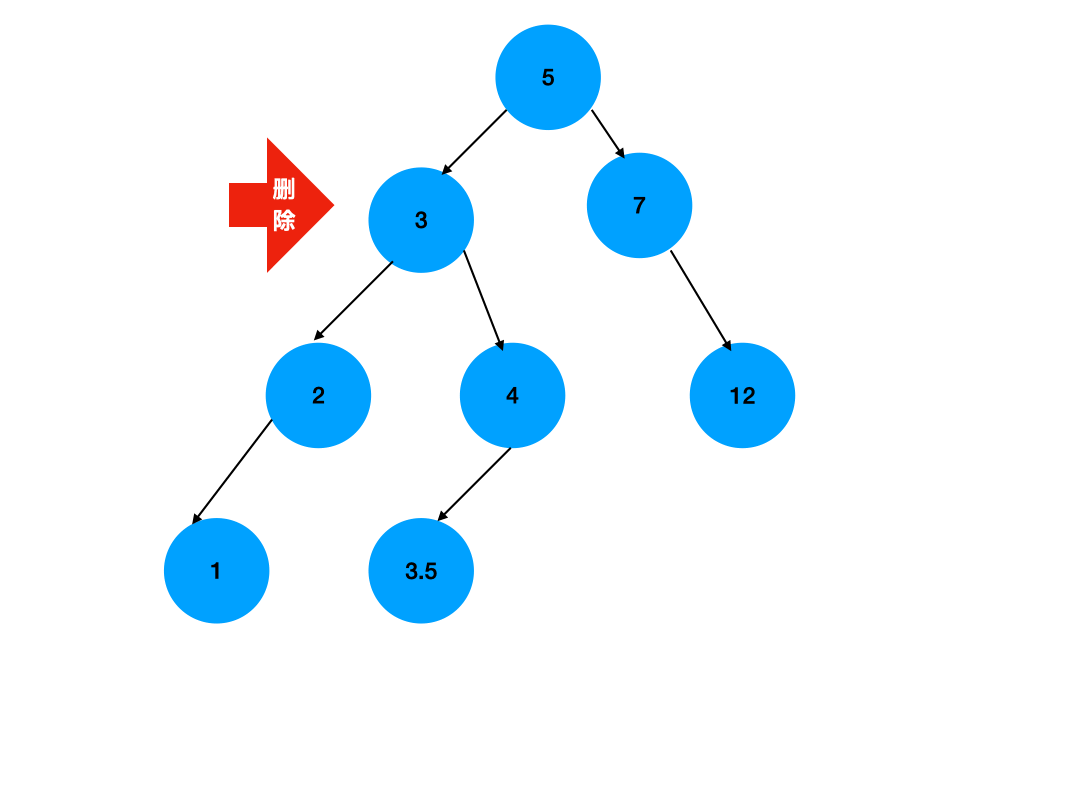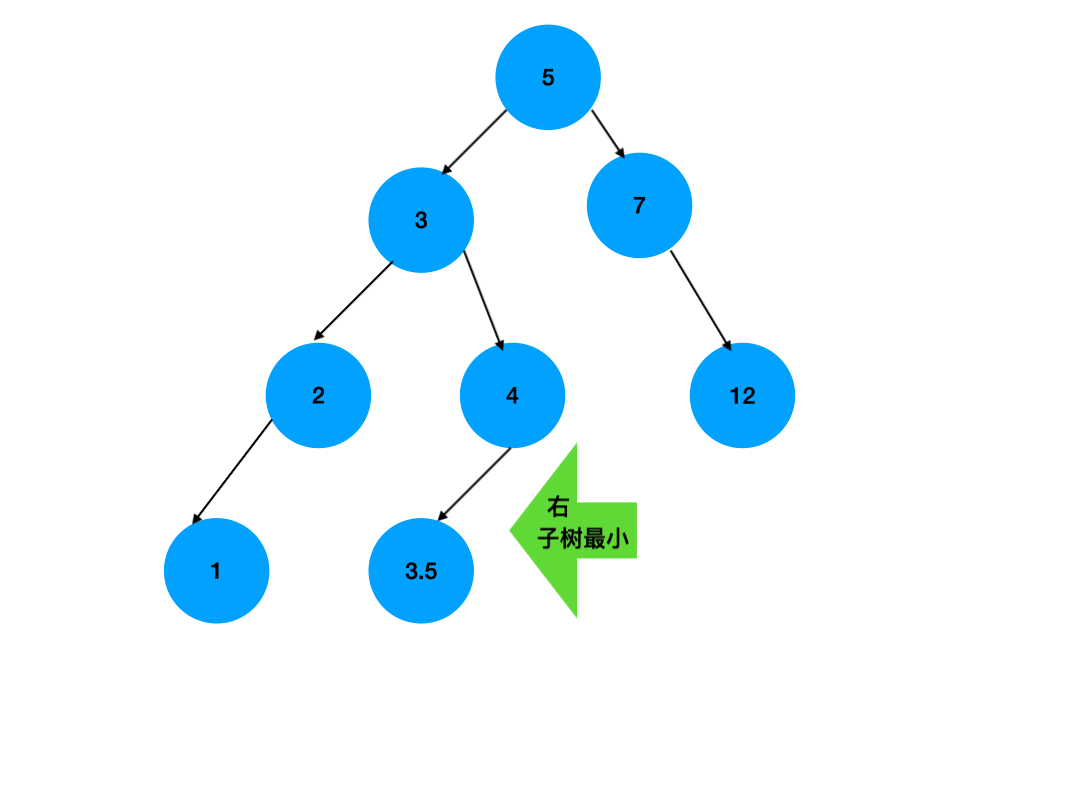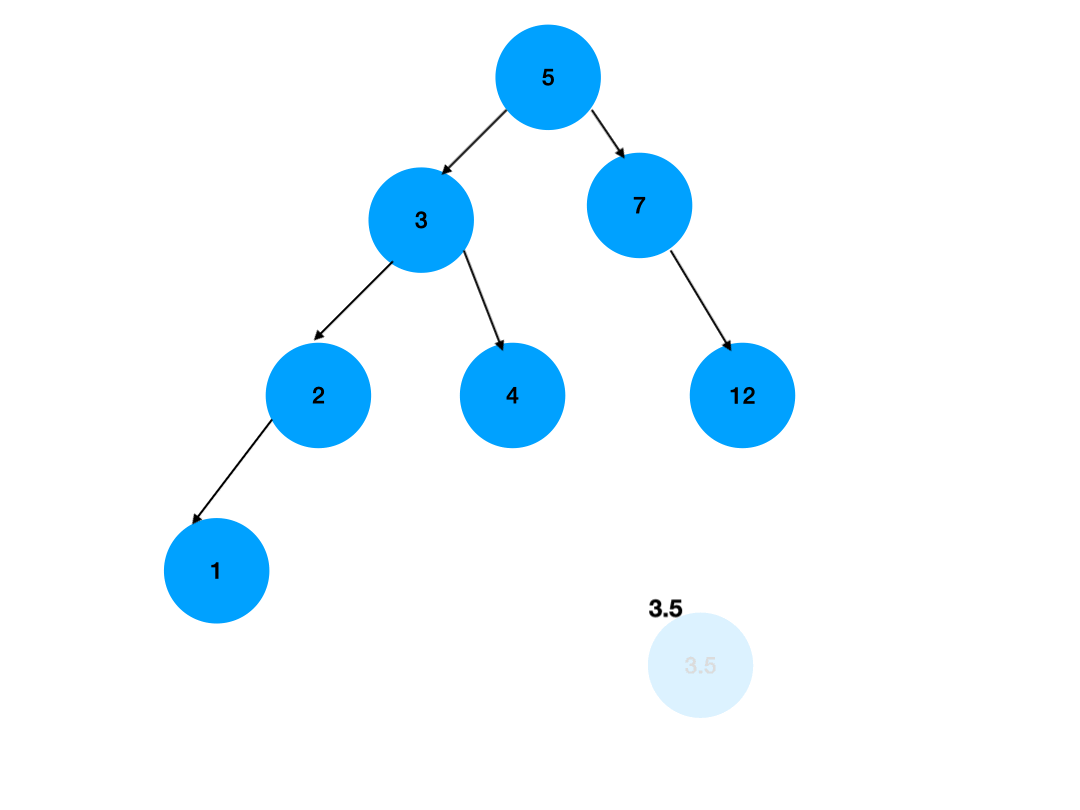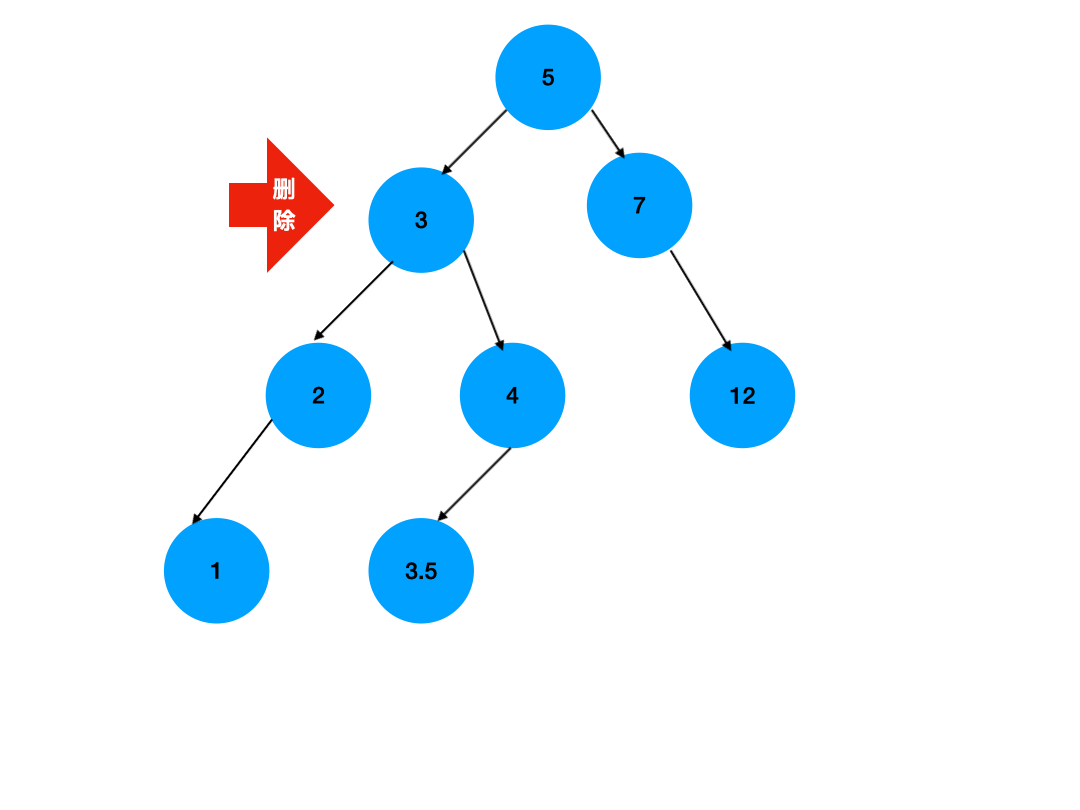
如图所示，我们先找到了将被删除的节点的右子树中的最小值，然后将其放在了将被删除的节点的值上，之后删除那个右子树上最小值的节点即可，其原理并不复杂，这是因为一颗二叉排序树的根节点，肯定是小于右子树上所有值，且大于左子树上所有值的，因此我们选用右子树上的最小值，替换根节点，仍然能满足这个条件，因为右子树上的最小值肯定大于其他值，并且一定大于左子树上的所有值，因此我们可使用右子树上的最小值进行替换，同理我们也可以使用左子树上的最大值进行替换，需要注意的是，右子树上的最小值和左子树上的最大值，要么是根节点，要么是一个仅有一棵子树的节点，在寻找左子树中的最大值时，我们只需要一股脑的往右找；在寻找右子树中的最小值时，我们则需要一股脑的往左找即可。
2.4.根节点的删除
当我们删除的节点是根节点时，我们需要先根据其parent来确认一下将要删除的节点是否时根节点，如果它是根节点，那么它的parent将是null，因此只要我们得到了一个parent值，其为null的话，那么我嗯将要删除的节点就是根节点，当树中只有一个节点的时候，也就是根节点就是叶子节点的时候我，我们仅需要将root置为null即可，如果当前根节点只有一个子树，我们将其子树的根节点赋予给root即可(root是当前结构内的根指针，是管理类中的字段)，而根节点有两个节点的时候，使用以上算法并没有什么影响，因为根字段的指向并没有变化，变化的是值，而被删除的节点时另外的节点，时右子树中值最小的节点，或者左子树中值最大的节点。
