算法学习——快慢指针与相遇问题
算法学习——快慢指针与相遇问题
摘要：在之前上大学时我就对算法十分怵头，记得其他同学们应该和我也差不多，每到算法课的时候总能听见一片开游戏的声音，考研二战失败之后我打算找工作，结果发现找工作还是绕不过算法，真是难受。在算法的初级学习中，我遇到了一个快慢指针问题，其中有一个难度稍高的问题我认为非常有意思，这让我再次深刻的认识到了算法的本质其实是数学原理，或者是数论之类的，也就是说，我不仅绕不过算法，还绕不过数学。这篇博客介绍了快慢指针与追击相遇问题。
1.问题题目以及模型分析
1.在一个无头节点链表中，判断这个链表是否成环。
2.如果这个链表有环，判断它的成环位置节点在哪里？
据说这是一个学校的数据结构中的考研自命题题目，其中第一道题在力扣中也有出现，第二题我目前没有在力扣中见到。看到这个题之后我的第一反应就是：408还是很人性化的。不管怎么说，让我们开始分析这道题目吧。
第一题是一个经典的追击相遇问题，说起追击相遇问题，我其实是有些印象的，在大三的算法课中，老师确确实实讲过这个问题，不仅如此，她还给我们讲了一个在二维水平面上的，较一维更复杂的追击问题，在最后她还扩展了维度，讲了一个三维空间中的追击相遇问题，只可惜当时我满脑子是白起上路怎么打芈月的这个问题，在此忏悔当时的不认真听讲。那么我们抛开二维和三维的追击相遇问题不谈，我们思考一下，一维上的追击相遇是什么情况呢？
1.一维无环追击相遇
如果有一条笔直的公路，没有终点，两个人同时从起点出发并一直匀速向前，A速度为4m/s，B速度为2m/s，这会发生什么？这会导致A和B唯一的一次见面，就是在起点，因为A的速度一直比B快，因此在这条笔直的路线中，A和B的距离会越拉越大，B无论如何也不会再追上A。因此在这种情况下：A和B从起点出发之后，将再也无法相遇。
这时我们换个思路，让速度较慢的B先出发20s，之后再让A从起点开始，这时会发生什么呢？A是否能追上B？答案是肯定的，因为A的速度更快，所以即使B有一个初位移，但由于A的速度，迟早A的位移会大于B（在这里我们不要讨论阿基里斯悖论，这不是极限问题）。我们简单的做一个计算：
Va = 4;//A的速度为4m/s
Vb = 2;//B的速度为2m/s
Bsb = 40;B的初始位移为40m
在此我们设未知数x，代表A开始之后，二者共同运动的时间
4x = 40 + 2x;
x = 20;//也就是说在A运动20s后，位移就会和B的位移一致，此时二者相遇
在二者相遇之后会发生什么呢？很遗憾，之后便什么也不会发生了，因为A的速度比B快，在二者相遇的那一刻，我们就可以将二者之前所做的一切位移做一个“波纹删除”，屏蔽掉二者之前的运动，仅仅从二者相遇这一点来看问题，我们很容易发现从二者相遇的这一点出发，这个问题就简化成了第一个情况，因为我们可以将二者相遇的位置当做是起点。
第三种情况是，我们让A先出发5s，然后再让B出发，这时B能追上A吗？答案显而易见，即使不让A先出发，让二者同时出发，B都追不上A，更别说让A先出发一截子了，B在这里当然是追不上A的。
所以，在此我们用一小段篇幅介绍了一个常识性的东西，那就是一维中最简单的追击相遇问题，我们得到了一个简单的常识：在匀速直线运动中，两个物体同时出发，在出发之后，速度慢的物体将永远无法追上速度快的物体；速度慢的物体先出发，速度快的物体迟早会追上速度慢的物体，在相遇之后，便可以将情况抽象为第一种情况，速度慢的物体将永远追不上速度快的物体；若速度快的物体先出发，二者将不存在相遇情况。
2.一维有环追击相遇
我在上面画这些篇幅分析无环追击，更多是为了反衬出有环追击问题的特殊，因为以上得到的一切常识，仅在直线运动中生效，一旦将两个物体放到一个环中，相遇问题就会发生改变。
不知大家在初高中上体育课的时候有没有跑过1000米或800米，一个班中肯定有这么几个跑得慢的，我的一个好朋友便是这种人，我跑完1000大概是3分20秒，他最多一次花了6分钟，记得有一次我在跑第二圈的时候，他竟然在我前面，意识到问题严重性的我，迫不及待的嘲讽了他一顿，因为他此时还在跑第一圈。好，这实际上就是快慢指针在一维有环情况下的追击问题了，如果一个一维路径变弯曲了，成为了一个环，那么走的快的物体，和走的慢的物体就有机会再次相遇了，最直观的例子就是表，当然不是液晶屏数字表，在普通的指针表中，我们会经常看到秒针扫过时针，分针；分针也经常和时针重合，这其实就是快慢指针的最直观体现。在一个环中，两个物体都只能一圈一圈的转圈，而不是一直向前，因此它们做的是一个周期运动，在走完一圈之后，它们还会按照相同的路径再走一圈，运动的慢的物体和运动的快的物体都在这个循环中，二者走的路径固然不同，但是这是一个周期运动，这个周期运动的移动路程可以写为：nT + x，n为走过的圈数，T为每圈的长度，x为当前圈从起点算起走过的路程长度，当跑完一圈，x便会等于T，这时x归零，n+1，代表跑了新的一圈，重新开始跑。而既然x代表从起点到终点走过的路程，那么只要两者x相等，就是相遇，不管两个物体的n是多少，简而言之：慢的物体还在跑上一圈的时候，快的物体进入了新的一圈，赶上了慢的物体。这种情况只在环状结构中出现，在直线结构中是无论如何也不会出现的。
2.在一个无头节点链表中，判断这个链表是否成环
1.详解
根据上一环节的模型分析，这道题迎刃而解。我们在这个链表中设置两个指针，或者说两个遍历节点(Java中不存在指针)，一个走的快，一个走的慢，然后让这两个指针不停的在链表中往前运动，如果这个链表中不存在环，那么这两个节点会一直往前运动，不会相遇，且最终会因为链表的有限长度而导致遍历结束，这种情况下，说明链表是没有环的。
而如果链表中存在环，两个指针会在遍历中双双进入环中运动，一旦进入环，整个遍历行为便无法结束，二者就会开始进行在环中的无尽奔波，在这个过程中，它们会有相遇的情况，因此在这里我们检测二者的相遇，只要是检测到了二者在整个遍历中发生了相遇情况，那么就说明这个链表有环。这里的阶梯思想其实也是抽象了上文中的模型分析结论：在直线运动中，如果快慢物体同时出发，则一定不存在相遇情况；但是在环中便会出现相遇情况。因此只要在这个过程中出现了相遇情况我们都可以断定这个链表是有环的。
2.代码
public boolean isCycleInLinkList(Node head,){
Node fast = head;//设置快遍历节点
Node slow = head;//设置慢遍历节点
while((fast.next!=null)&&(fast!=null)){//这两个终止条件是针对链表长度奇数个或者偶数个的
fast = fast.next.next;//快指针更快
slow = fasr.next;
if(fast == slow){//二者相遇时则停止
return true;
}
}
return false;
}
3.如果这个链表有环，判断它的成环位置节点在哪里？
这个问题就麻烦了，反正我刚看见的时候是一点也不会。然后别人直接给我抛来了一个解题方法，但是我理解不了为什么这么解题，进而陷入苦想，在经历了几个小时的思考之后，我终于推导了出来，现在我将解题思路放在这里，需要注意的是，这里存在一个可以拿来被复用的思想，或者说是公理，尽管不是我推导出来的(我怀疑这可能是一个古典数学理论)，现在我们开始再推导一次。
1.详解
首先我们假设，指针在移动的过程中是在链表的x位置处进入环的，并且，二者在进入环之后，在慢指针移动了n个位置之后，发生了第一次相遇，也就是说如下图中，二者在Z点发生了相遇：
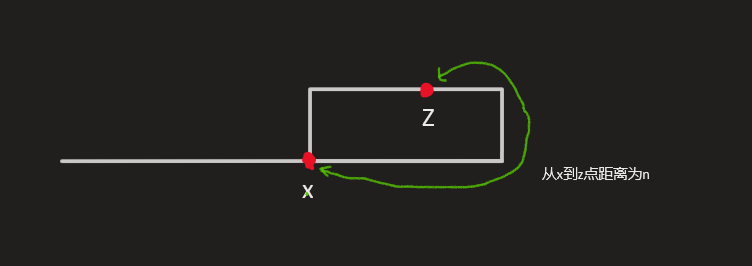
我们设从起点到X点的距离是x，因此当在第一次相遇的时候，慢指针的路程是x+n，而因为快指针的速度是慢指针的一倍，它们从头开始，运动时间就是完全一致的，因此当二者发生相遇的时候，有如下几点值得注意：1.当二者发生相遇时，慢指针一定已经进入了环中；2.快指针一定先于慢指针进入环中；3.快指针移动过的路程累计是慢指针的1倍，也就是2*（x+n），其中早在路程为x时，快指针已经进入了环，它在环中运动了x+2n的路程。
同时我们根据二者在Z点相遇还能推断出的是：在Z点时，慢指针的路程是x+n，快指针的路程是2*(x+n)，说明此时快指针比慢指针多走了x+n，这同时也说明，从Z处开始，继续往后推移x+n个距离，可以再次回到Z点，因此x+n的距离至少是环一巡距离的一倍。因此我们引出了一个有用的公理：慢指针和快指针在环中第一次相遇时的路程差值，是环路程的倍数。如果将这个问题放到一个实际的链表中，我们是可以选择在二者第一次相遇的时候停止while循环并且取得二者相遇位置的，也就是说Z点实际上对我们来说是已知的，那我们如何根据已知的Z点得到未知的X点呢？有趣的东西来了：x = （x + n）- n，我们不知道n是多少，我们也不知道x是多少，但是，我们知道，慢指针从原点出发，走了x个单位达到了环的开始位置X，而从Z点开始，我们往后退n个元素，也会抵达X位置，可是我们现在既不知道n，也不知道x，我们怎么办呢？这是我们使用钟表指针原理，既然一巡是x+n，那么在环中进行研究的话，从X位置开始，往后移动一巡，仍然是x位置，如果是从链表表头开始出发，进入环后，走一圈的距离就是2x+n，我们在此过程中唯一已知的一点位置是x+n，我们会发现正好x+n再往后移动x个位置，就是2x+n，也就是说：从我们已知的这个点开始移动x个单位之后，最终会抵达X位置，而从链表表头开始移动x个单位，最终也会抵达X位置，如果此时存在两个指针，一个指针从链表表头开始移动，另一个从Z位置开始移动，二者在移动x个位置之后一定会在X位置相遇。因此这时我们只要将快指针的速度调到和慢指针的速度一致，并且让其中一个指针从头开始遍历，让另一个指针从Z位置开始遍历，在进行同样次数的x次循环之后，二者必定会相遇一次，所以我们就可以得出结论：在二者第一次相遇之后，让其中一个指针指回链表头结点，然后二者一起匀速运动，直到二者相遇，就是环开始的位置。
根据上述分析，我们得到了这道题的算法流程：
1.使用第一题的算法，找到快慢指针的第一次相遇位置。
2.快慢指针中的其中一个直接指向链表原点，快指针移动速度降低为每一一个单位。
3.二者同时运动，直到二者第一次相遇时停止，这是二者的相遇位置，便是链表成环的位置。
2.代码
public Node findWhereMakeCycle(Node head){
Node fast = head;
Node slow = head;
while((fast.next != null)&&(fast != null)){
fast = fast.next.next;
slow = slow.next;
if(fast == slow){//二者相遇时，进入第二步
slow = head;//慢节点回到头部
while(fast != slow){//驱动二者同步运动的循环
fast = fast.next;
slow = slow.next;//二者每一运动相同的单位
}
return fast;//二者相遇后，二者均会指向成环节点
}
}
return null;//要是从这返回了说明链表没有环，因此也就没有成环节点，返回null
}
