希尔排序详解
希尔排序详解
摘要：插入排序固然是个好排序，因为它的排序效率是和数组状态挂钩的，它的最好情况时间复杂度很理想，但是它存在一个巨大的问题，那就是在整个数组的前n-1个数字都有序，唯独最后一个数字的存在导致整个数组无序时，会出现比较严重的浪费现象，因此人们更新了插入排序，并命名这种更新的方法为希尔排序，接下来我们详细介绍希尔排序。
1.插入排序存在的问题
插入排序是一种很不错且简单易懂的排序方法，但是插入排序存在一种比较致命的弊端，这种弊端会使其效率大大降低，当数组为这种情况的时候，插入排序会进行大量的无意义操作：
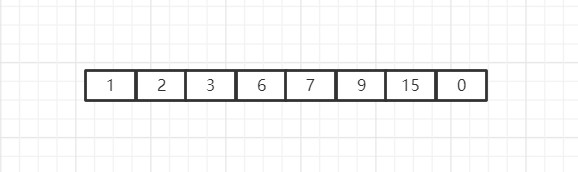
就是当一个数组的前边大部分数字都是有序的，就最后这一个的存在导致数组乱序时，使用插入排序，会在前边这些数字身上浪费大量的时间，因为前边的数字们都是有序的，可是要想检测到最后一个数字0，不仅要空转一些无意义的循环，且要进行无意义的对比，最为致命的是，当循环轮到最后一个数字之后，还要进行n次循环，这就显得更加致命了，明明整个数组除了最后一个元素都没问题，现在在排序的时候不仅要空转几个循环，最后一个元素还要一个一个的通过n次循环前移，明明我们直接让最后一个元素直接蹦到第一个就可以一下子解决，现在我们却要进行那么多步骤浪费那么多时间。
通过上述情况我们可以发现，在插入排序中存在一个有可能让时间复杂度升高的机制，那就是新插入的元素往前移动的这个机制，因为这个机制被处理的非常像冒泡排序，因此当需要往前移动n个位置时，它必定需要n轮循环，这个机制在某些情况下，如上面提到得我情况，会变得非常没有意义，因此人们对于这个算法提出了改进，这个改进后的排序算法就是希尔排序。
2.希尔排序的图解
希尔排序的进步之处在于，它内部定义了名为步长的概念，那什么是步长，希尔排序又是怎样进行的呢？我们这就来通过画图的方式来进行详细解释。
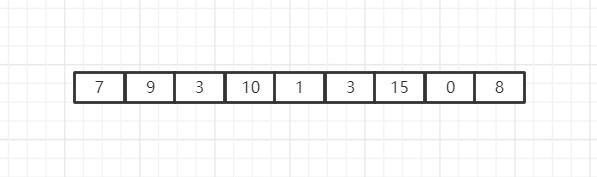
现在我们得到了一个如图所示的无序数组，我们要对其进行排序，实际上，希尔排序的内核排序算法仍然是插入排序，所以我们现在应该直接对这个数组进行插入排序吗？并不是，希尔排序尽管内核和插入排序一样，但是希尔排序自己还是有东西的，它添加了一种名为步长的概念，在拿到一个待排序的数组时，希尔排序确实要对它使用插入排序的理念进行排序，但是它并不会直接对整个数组进行插入排序，而是按照步长将整个数组分成多个子数组，对子数组进行插入排序。那么这个根据步长划分子数组是怎么分的呢？我们以这个数组为例，根据观察我们可以知道该数组长度是9，那么步长应该设置成多少合适呢？希尔排序中，第一次子数组排序的步长为9/2，然后向下取整，也就是4，现在我们需要根据步长4来进行子数组的划分：
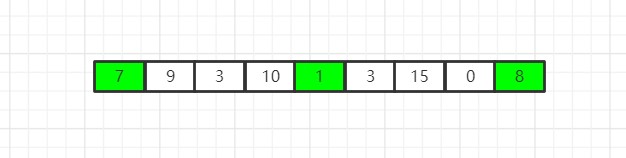
有了这张图，是不是更加明了了？所谓步长，实际上就是遍历时，指针每次自增的数量，通常我们在遍历一个数组的时候，指针每次要自增1，这样才能遍历整个数组，也就是说我们平时使用的数组遍历，实际上就是步长为1的遍历，而这时，我们使用步长为4的遍历，而根据步长为4的遍历方法，我们就获得了第一个子数组，也就是被标记为绿色的子数组，这个数组就显得比较简单且跨度很大，因此当出现这种情况时：
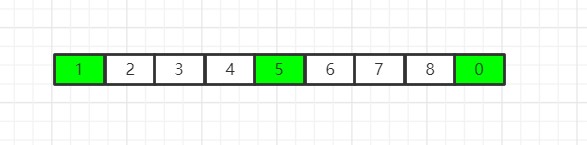
就可以非常轻松的使用插入排序将0往前移动很多位置，而不需要再进行n轮循环，以1为步长将其移动8次。在此之后，我们不仅要以第一个元素为开头进行分组，我们还要以之后的元素为开头进行分组，可以被当做子数组开头的元素，截止到第四个位置，也就是9/2的前一个位置，这是根据数学计算得到的：
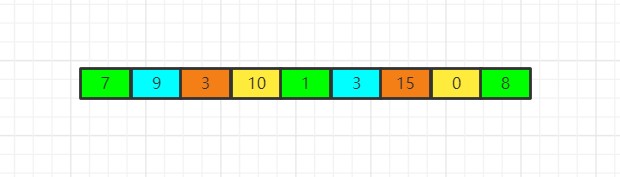
现在我们已经按照每次自增4的步长进行了分组，每种颜色都代表一个子数组：{7,1,8}，{9,3}，{3,15}，{10,0}，根据步长进行好分组之后，我们就要依次对这些子数组使用插入排序，由于大步长的划分，使得这些子数组们的规模都不大，因此使用起插入排序来十分快速方便，现在我们展示每个子数组已经被排好序的状态：
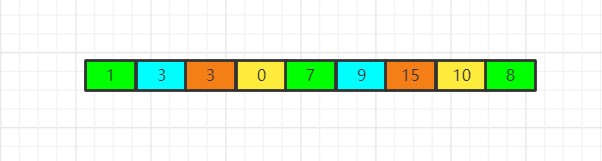
这个数组看上去似乎已经比以前有些顺序了，但是现在它并不完全是有序的，这说明为4的步长并不能保证让整个数组变得有序，我们还需要步长更细致的分组并根据这个更细致的步长再来一次，步长每次需要减少1倍，也就是说，新步长应该是4 / 2 = 2:
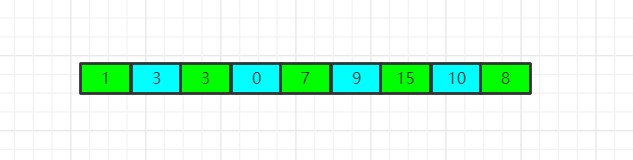
如图所示，根据新步长划分的子数组，现在只有两个了，即绿色部分和蓝色部分，现在我们对这两个子数组再分别进行一次插入排序，结果如图：
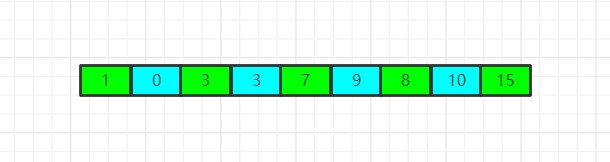
如图所示，现在的就只有下标为0和下标为1的两个位置无序了，整个数组已经变得趋于有序了，这同时也说明：步长为2并不能完全让这个数组变得有序，到了还是需要步长为1，因此我们现在使用步长1进行分组，并进行插入排序，实际上就是对当前状态的这个数组进行插入排序：
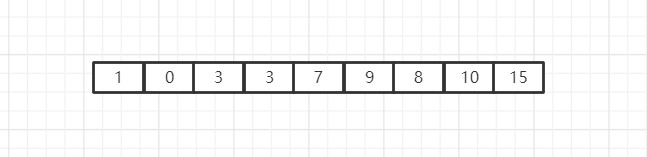
我们现在直接对这个数组进行希尔排序，我们可以发现，在使用步长为1的希尔排序时，这个数组中不存在那种比较小的数字在最后边的情况了，这里即使是0，也是非常的靠前，只需移动一次，0即可抵达自己的正确位置，而不再出现那种0需要往前移动n位的情况了。我们可以发现，在原数组中，0本来是在倒数第二位，也就是说如果使用普通的插入排序，0移动到自己的正确位置，需要7轮循环，可是这里由于大步长设置，0移动到正确位置，只进行了3次循环，即步长为4时，进行了一次循环，步长为2时，进行了一次循环，步长为1时，进行了一次循环，在大步长时，0一次循环就可以往前移动很多位置，希尔排序显现出了对于解决小元素位置靠后的这种情况的极大优势，很好的解决了插入排序需要大量循环解决小元素前移的问题。
希尔排序实际上就是通过设置步长概念，先设置一个比较大的步长，通过比较小的代价，将数组中位置靠后的小值元素移动到前边，虽然数组让然无序，但是小值元素基本上都在靠前的位置，且由于这是步长很大，移动它们不需要大量的循环；之后我们再缩小步长，进而让子数组划分趋于简单，让数组整体趋于有序，同时也是再让小元素们进一步更加准确的向前移动；直到最后，我们将步长缩小为1，这时整个数组已经趋于有序，可能大部分元素已经正确归位了，但是还是有一小部分元素仍然没有抵达自己的正确位置，而此时的数组由于之前的处理，已经趋于有序且小元素一定都在非常靠前的位置，因此这时使用步长为1的插入排序，不会出现那种小元素大量前移才能抵达自己正确位置的情况，且此时的数组已经趋于有序，插入排序的时间复杂度会非常低，进而最终将整个数组快速准确的排好序。
3.希尔排序代码详解
希尔排序看上去有些复杂，而且是插入排序的扩充，但实际上它的代码实现并不复杂，只要我们学会了插入排序，只要稍加改造，就可以得到一个希尔排序：
public static void shellSort(int[] arr){
for(int gap = arr.length/2; gap>0; gap/=2){//设置步长，并通过一个循环来驱动步长逐渐减小
for(int i = gap;i<arr.length;i++){//被改造的插入排序，现在为gap的位置，之前在插入排序中都是1
/*
i为gap，i每次自增1，为什么i每次自增1呢，因为这个循环代表的是：对每一个子数组都进行一次插入排序,
也就是说：实际上在上图中就代表着指向子数组头的指针往下加了一个，指向了另外一个颜色的子数组，当i
自增1时，说明i指向了下一个分组的数组，开始对那个数组进行插入排序了。这里需要注意的是：该算法并不
是将一个子数组完全排好序之后，在指向下一个数组的，而是排好当前子数组在i之前的部分，就立刻指向下一
个子数组，当前子数组的i后边的元素并没有排序。这是因为i的自增不仅要考虑当前整个子数组的情况，也要
考虑其他子数组的情况，所以采取了每次加1的策略，而随着i的不断向后推进，i迟早会指向之前没有排好序的
子数组中的后边的元素，并重新对值之前没有排好序的子数组再进行排序，这样i遍历完从gap到最后一个节点
时，就可以不仅完成了对所有子数组的遍历，也完成了对于所有子数组的排序。整体上，我们在理解算法的时
候，可以理解为先给一个子数组排序，再给下一个子数组排序，但是在代码中，给每个子数组的排序行为不是
一下子就拍好了它可能先给子数组A排了一半，就去给子数组B排序了，当给子数组D排完序之后，它又指向了子
数组A的之前没有排过序的一个元素，这时，它又会给子数组A进行继续排序，直到i指向了数组尾，此时，i一
定是已经经历了所有的子数组，并且经历了所有的在gap之后的子数组节点，它这时就完成了所有的子数组排序了。
*/
for(int j = i - gap; j>=0; j-=gap){//插入排序的内循环，就是插入排序中的往有序数组中插入数据的过程，只不过之前写死的步长1，现在改成了灵活的步长gap变量，其余算法思路一样。
if(arr[j] > arr[j+gap]){
int temp = arr[j+gap];
arr[j+gap] = arr[j];
arr[j] = temp;
}else
break;
}
}
}
System.out.println(Arrays.toString(arr));
}
希尔排序的思想理解起来可能比较简单，而其算法理解起来可能和思想有些出入，因此我在这里再记录一次：希尔排序是插入排序的改版，其核心代码非常相似，但是希尔排序被赋予了更多的意义与功能，其中原插入排序中控制有序数组与无序数组分界线的那个循环，现在不仅是控制有序数组与无序数组的分界线了，它还负责控制子数组的变化，因此它不能像其他与步长有关的变量一样，一次增加步长的长度，而是仍然要每次自增1，这就导致每个子数组的排序并不能在一次循环中完成，一次循环只能让当前子数组的，i指针指向的元素之前的部分完成排序，当i+1之后，排序面向的对象就是下一个子数组了，但是i每次自增1，迟早会再次遇见之前没有完成排序的子数组并最终对其再实施一次排序，而当i移动到到最后边后，也就意味着i一定遇见过了所有子数组的元素，此时它一定完成了所有子数组的排序。在此使用这个算法，变量i每完成所有轮循环，就会对当前步长为gap而划分的子数组们完成一次排序，而最外层循环，是控制步长的，每一轮循环都会让步长缩短，进而使其内部的插入排序更加精确，直到步长为1时，内部的排序就会变成一个普通的插入排序，但是由于此前的大步长准备，这时的数组已经变得对插入排序非常友好，进而可以让最后的也是最精确的一次排序能够快速的完成。
希尔排序理解起来虽然有这个那个的困难，但是它写起来很简单，只要我们会写插入排序，并将插入排序包裹在一个步长缩减循环中，再修改原来的步长1为变量gap即可。以上就是希尔排序的详细解读。
