总结分享 | 动态规划经典例题总结三

题目

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

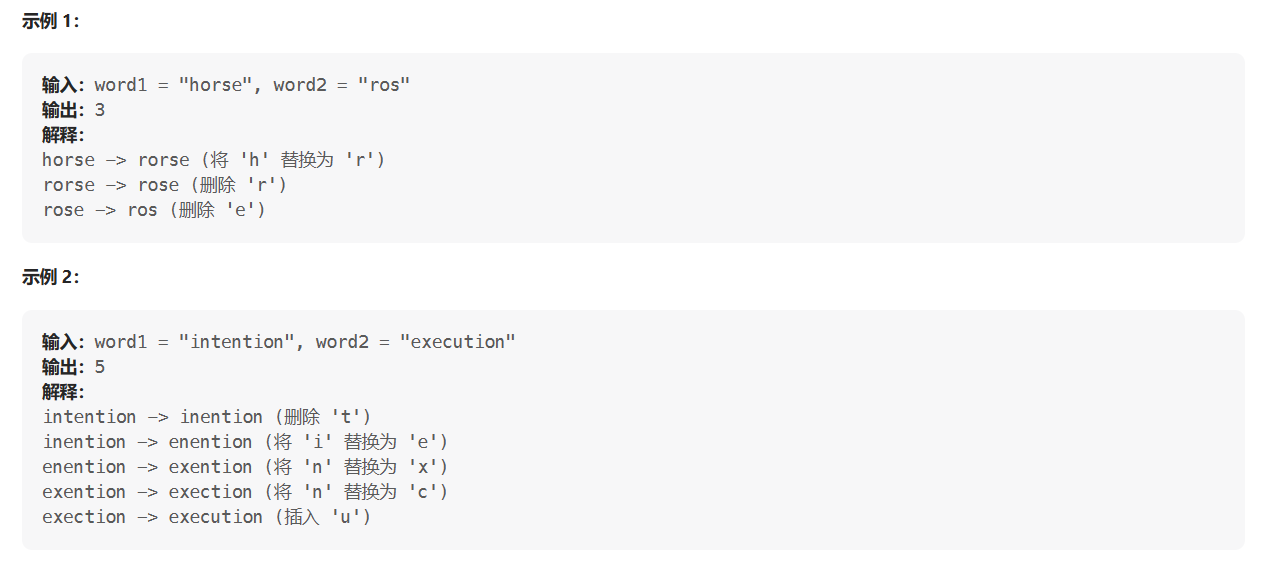
提示：

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

解题思路

一、定义数组元素的含义

由于我们的目的求将 word1 转换成 word2 所使用的最少操作数 。那我们就定义 dp[i] [j]的含义为：当字符串

word1 的长度为 i，字符串 word2 的长度为 j 时，将 word1 转化为 word2 所使用的最少操作次数为 dp[i] [j]。

二、找出关系数组元素间的关系式

接下来我们就要找 dp[i] [j] 元素之间的关系了，比起其他题，这道题相对比较难找一点，但是，不管多难找，大部

分情况下，dp[i] [j] 和 dp[i-1] [j]、dp[i] [j-1]、dp[i-1] [j-1] 肯定存在某种关系。因为我们的目标就是，从规模小

的，通过一些操作，推导出规模大的。对于这道题，我们可以对 word1 进行三种操作

由于我们是要让操作的次数最小，所以我们要寻找最佳操作。那么有如下关系式：

一、如果我们 word1[i] 与 word2 [j] 相等，这个时候不需要进行任何操作，显然有 dp[i] [j] = dp[i-1] [j-1]。（别忘了 dp[i] [j] 的含义哈）。

二、如果我们 word1[i] 与 word2 [j] 不相等，这个时候我们就必须进行调整，而调整的操作有 3 种，我们要选择

一种。三种操作对应的关系试如下（注意字符串与字符的区别）：

1. 如果把字符 word1[i] 替换成与 word2[j] 相等，则有 dp[i] [j] = dp[i-1] [j-1] + 1;
2. 如果在字符串 word1末尾插入一个与 word2[j] 相等的字符，则有 dp[i] [j] = dp[i] [j-1] + 1;
3. 如果把字符 word1[i] 删除，则有 dp[i] [j] = dp[i-1] [j] + 1;

那么我们应该选择一种操作，使得 dp[i] [j] 的值最小，显然有

dp[i] [j] = min(dp[i-1] [j-1]，dp[i] [j-1]，dp[[i-1] [j]]) + 1;

三、找出初始值

当 dp[i] [j] 中，如果 i 或者 j 有一个为 0，那么还能使用关系式吗？答是不能的，因为这个时候把 i - 1 或者 j - 1，就变成负数了，数组就会出问题了，所以我们的初始值是计算出所有的 dp[0] [0….n] 和所有的 dp[0….m] [0]。这个还是非常容易计算的，因为当有一个字符串的长度为 0 时，转化为另外一个字符串，那就只能一直进行插入或者删除操作了。

一个空串和一个非空串的编辑距离为 dp[i][0] = i 和 dp[0][j] = j，dp[i][0] 相当于对 word1 执行 i 次删除操作，dp[0][j] 相当于对 word1执行 j 次插入操作。

代码

public int minDistance(String word1, String word2) {
    int n = word1.length();
    int m = word2.length();

    // 有一个字符串为空串的情况
    if (n * m == 0) {
        return n + m;
    }

    // dp数组
    int[][] dp = new int[n + 1][m + 1];

    // 边界状态初始化
    for (int i = 0; i < n + 1; i++) {
        dp[i][0] = i;
    }
    for (int j = 0; j < m + 1; j++) {
        dp[0][j] = j;
    }

    // 计算所有 dp 值
    for (int i = 1; i < n + 1; i++) {
        for (int j = 1; j < m + 1; j++) {
            int left = dp[i - 1][j] + 1;
            int down = dp[i][j - 1] + 1;
            int left_down = dp[i - 1][j - 1];
            if (word1.charAt(i - 1) != word2.charAt(j - 1)) {
                left_down += 1;
            }
            dp[i][j] = Math.min(left, Math.min(down, left_down));
        }
    }
    return dp[n][m];
}