感知机笔记

目录

• 感知机定义
• 数据集的线性可分
• 感知机学习策略
• 感知机学习算法
  • 原始形式
  • 对偶形式
• 小结

---

感知机模型

感知机定义

假设输入空间(特征空间)是\(\chi \subseteq {R^n}\),输出空间是\(\gamma = \{ + 1, - 1\}\).输入\(x \in \chi\)表示实例的特征向量，对应于输入空间(特征空间)的点：；输出\(y \in \gamma\)表示实例的类别。由输入空间到输出空间的函数，如下：

\[f(x) = sign(w \bullet x + b) \]

称为感知机，其中，\(w \in {R^n}\)叫作权值或权值向量，\(b\)叫作偏置(bias)，\(sign\)为符号函数。

感知机是一种线性分类模型，属于判别模型。感知机模型的假设空间是定义在特征空间中的所有线性分类模型或线性分类器，即函数集合\(\{ f|f(x) = w \bullet x + b\}\).

感知机的几何解释：线性方程

\[w \bullet x + b = 0 \]

对应于特征空间\({R^n}\)中的一个超平面\(S\)，其中，\(w\)是超平面的法向量，\(b\)是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部分的点(特征向量)分别被分正、负两类。因此，超平面S称为分离超平面。

感知机学习，由训练数据集(实例的特征向量及类别)

\[T{\rm{ = \{ (}}{{\bf{x}}_1}{\rm{,}}{{\rm{y}}_1}{\rm{),(}}{{\bf{x}}_2}{\rm{,}}{{\rm{y}}_2}{\rm{)}},...,{\rm{(}}{{\bf{x}}_N}{\rm{,}}{{\rm{y}}_N}{\rm{)\} }} \]

感知机预测，通过学习得到的感知机模型，对于新的输入实例给出对应的输出类别。

数据集的线性可分

给定数据集，如果存在一个超平面能够将数据集的正实例点和负实例点完全分开，则称数据集是线性可分的，否则不可分。

感知机学习策略

感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全分开得分离超平面。为了找出这样得超平面，即确定感知机模型参数\(w，b\)，需要确定一个学习策略，即定义(经验)损失函数并将损失函数极小化。

输出空间\(R^n\)中任一点\(x_0\)到超平面\(S\)的距离:

\[\frac{1}{{\left\| w \right\|}}(w \bullet {x_0} + b) \]

对于误分类的数据\(({x_i},{y_i})\)来说，总有\(- {y_i}(w \bullet {x_i} + b) > 0\)成立。

这样，假设超平面\(S\)的误分类点集合为\(M\)，那么所有误分类点到超平面\(S\)的总距离为

\[- \frac{1}{{\left\| w \right\|}}\sum\limits_{{x_i} \in M} {{y_i}(w \bullet {x_i} + b)} \]

不考虑\(\frac{1}{{\left\| w \right\|}}\),就得到感知机学习的损失函数。即

\[L(w,b) = - \sum\limits_{{x_i} \in M} {{y_i}(w \bullet {x_i} + b)} \]

感知机学习算法

原始形式

感知机学习算法是误分类驱动的，具体采用随机梯度下降法。首先，任意选取一个超平面\(w_0,b_0\)，然后用梯度下降法不断地极小化目标函数。极小化过程不是一次使\(M\)中的所有误分类点的梯度下降，而是一次随机选取一个误分类点使梯度下降。

• 损失函数的梯度：

\[{\nabla _w}L(w,b) = - \sum\limits_{{x_i} \in M} {{y_i}{x_i},} {\nabla _b}L(w,b) = - \sum\limits_{{x_i} \in M} {{y_i}.} \]

• 更新方式：

\[w \leftarrow w + \eta {y_i}{x_i},b \leftarrow b + \eta {y_i} \]

随机选取一个误分类点\(({x_i},{y_i})\)进行参数更新，\(\eta (0 < \eta \le 1)\)是步长，在统计学习中又称为学习率。这样通过迭代可以期待损失函数\(L(w,b)\)不断减小，直到为0.

解： 构建最优化问题：

\[\mathop {\min }\limits_{w,b} L(w,b) = - \sum\limits_{{x_i} \in M} {{y_i}(w \bullet {x_i} + b)} \]

按照上述算法，求出\(w,b\)即可，为了方便令\(\eta {\rm{ = 1}}\).
(1)取初值\({w_0} = 0,{b_0} = 0\)
(2)对\({x_1} = {(3,3)^T},{y_1}({w_0} \bullet {x_1} + {b_0}) = 0\),未能被正确分类，更新\(w,b\)：

\[{w_1} = {w_0} + {y_1}{x_x} = {(3,3)^T},{b_1} = {b_0} + {y_1} = 1 \]

得到线性模型

\[{w_1} \bullet x + {b_1} = 3{x^{(1)}} + 3{x^{(2)}} + 1 \]

(3)对\(x_1,x_2\)，显然，\({y_i}({w_1} \bullet {x_i} + {b_1}) > 0\)被正确分类，不修改\(w，b\)
对\({x_3} = {(1,1)^T},{y_3}({w_1} \bullet {x_3} + {b_1}) < 0\),更新\(w,b\)：

\[{w_2} = {w_1} + {y_3}{x_3} = {(2,2)^T},{b_2} = {b_1} + {y_3} = 0 \]

得到线性模型

\[{w_2} \bullet x + {b_2} = 2{x^{(1)}} + 2{x^{(2)}} \]

如此继续下去，直到

\[\begin{array}{l} {w_7} = {(1,1)^T},{b_7} = - 3 \\ {w_7} \bullet x + {b_7} = {x^{(1)}} + {x^{(2)}} - 3 \\ \\ \end{array} \]

对所有数据点\({y_i}({w_7} \bullet {x_i} + {b_7}) > 0\),没有误分类点，损失函数达到极小。
分离超平面为：\({x^{(1)}} + {x^{(2)}} - 3 = 0\)
感知机模型为：\(f(x) = sign({x^{(1)}} + {x^{(2)}}{\rm{ - }}3)\)

• python验证

import numpy as np
X=np.array([[3,3],
           [4,3],
           [1,1]])
Y=np.array([[1],
           [1],
           [-1]])
#初始化
w_0,b_0=[0,0],0
stop_sign="start"
while stop_sign:
    m,_=X.shape
    for i in range(m):
        x=X[i,:]
        y=Y[i]
        temp=(w_0@x+b_0)*y
        if temp<=0:
            #更新参数设定
            w_0+=y*x
            b_0+=y
            #w_0,b_0=updateParams(x,w_0,b_0,y)
            sign=str(i)
            print("误分类点：","x"+sign,", w：",w_0,"b：",b_0[0],"超平面：",str(w_0[0])+"*x^(1)+"+str(w_0[1])+"*x^(2)+"+str(b_0[0]))
            break
    else:
        stop_sign=""

输出结果：

误分类点： x0 , w： [3 3] b： 1 超平面： 3*x^(1)+3*x^(2)+1
误分类点： x2 , w： [2 2] b： 0 超平面： 2*x^(1)+2*x^(2)+0
误分类点： x2 , w： [1 1] b： -1 超平面： 1*x^(1)+1*x^(2)+-1
误分类点： x2 , w： [0 0] b： -2 超平面： 0*x^(1)+0*x^(2)+-2
误分类点： x0 , w： [3 3] b： -1 超平面： 3*x^(1)+3*x^(2)+-1
误分类点： x2 , w： [2 2] b： -2 超平面： 2*x^(1)+2*x^(2)+-2
误分类点： x2 , w： [1 1] b： -3 超平面： 1*x^(1)+1*x^(2)+-3

对偶形式

对偶形式的基本思想是，将\(w,b\)表示为实例\(x_i\)和标记\(y_i\)的线性组合的形式，通过求解其系数而求得\(w,b\)。在原始形式中可假设初始值为0，根据误分类点逐步修改\(w,b\),设修改\(n\)次，则\(w,b\)关于\(({x_i},{y_i})\)的增量分别是\({\alpha _i}{y_i}{x_i},{\alpha _i}{y_i}({\alpha _i} = {n_i}\eta )\),最后学习到\(w，b\)可以表示为：

\[w = \sum\limits_{i = 1}^N {{\alpha _i}{y_i}{x_i}} ,b = \sum\limits_{i = 1}^N {{\alpha _i}{y_i}} \]

对偶形式中训练实例仅以内积的形式出现，为了方便，可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储，这个矩阵就是所谓的Gram矩阵，

\[G = {[{x_i} \bullet {x_j}]_{N*N}} \]

对偶形式对应的算法：

上述案例的对偶形式解法：

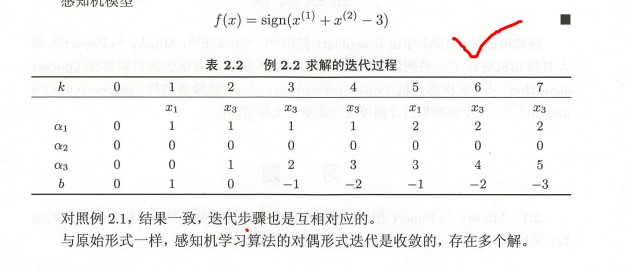
• Python验证

import numpy as np

def calAndUpdateParams(result,alpha,y,b):
    result=np.dot(result,alpha)+y*b
    #更新参数
    sign=""
    for num,i in enumerate(result):
        if i<=0:
            alpha[num]+=1
            b=y[num]+b
            #第几个样本点误分
            sign="x"+str(num+1)
            #print("num:",num,"b:",b)
            break
    print("误分样本点：",sign," , alpha: ",alpha.tolist()," , b  :",b,end=" ")
    return alpha,b,sign

X=np.array([[3,3],
           [4,3],
           [1,1]])
y=np.array([[1],
           [1],
           [-1]])
alpha=np.zeros_like(y)

#内积矩阵
gramMat=np.zeros((3,3))
m=X.shape[0]
for i in range(m):
    for j in range(m):
#         print(X[i,:],X[j,:], sum(X[i,:]*X[j,:]))
        gramMat[i,j]=sum(X[i,:]*X[j,:])
    
result=np.dot(y,y.T)*gramMat 
#初始化
eta,b=1,0

stop_sign="start"
while stop_sign:
    alpha,b,stop_sign=calAndUpdateParams(result,alpha,y,b)
    print("\n")

输出结果：

误分样本点： x1  , alpha:  [[1], [0], [0]]  , b  : [1] 
误分样本点： x3  , alpha:  [[1], [0], [1]]  , b  : [0] 
误分样本点： x3  , alpha:  [[1], [0], [2]]  , b  : [-1] 
误分样本点： x3  , alpha:  [[1], [0], [3]]  , b  : [-2] 
误分样本点： x1  , alpha:  [[2], [0], [3]]  , b  : [-1] 
误分样本点： x3  , alpha:  [[2], [0], [4]]  , b  : [-2] 
误分样本点： x3  , alpha:  [[2], [0], [5]]  , b  : [-3] 
误分样本点：   , alpha:  [[2], [0], [5]]  , b  : [-3]

---

小结

• 感知机学习的策略是极小化损失函数:

\[\mathop {\min }\limits_{w,b} L(w,b) = - \sum\limits_{{x_i} \in M} {{y_i}(w \bullet {x_i} + b)} \]

损失函数对应于误分类点到分离超平面的总距离

• 感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法，有原始形式和对偶形式。算法简单易于实现。原始形式中，首先任意选取一个超平面，然后用梯度下降法不断极小化目标函数。在这个过程中随机选取一个分类点使其梯度下降。

• 当训练数据集线性可分时，感知学习算法是收敛的。感知机算法在训练数据集上的误分类次数\(k\)满足不等式:

\[k \le {(\frac{R}{\gamma })^2} \]

当训练数据集线性可分时，感知机学习算法存在无穷多个解，其解由于不同的初值或不同的迭代顺序而可能有所不同。

---

异或问题

Minsky与Papert指出：感知机因为是线性模型，所以不能表示复杂函数，如异或(XOR),验证感知机为什么不能表示异或。

#验证异或问题
import numpy as np
import matplotlib.pyplot as plt
import time
X=np.array([[0,0],
           [0,1],
           [1,1],
           [1,0]])
Y=np.array([[-1],[1],[-1],[1]])

x_plot=np.linspace(0,1,50)
fig,ax=plt.subplots()
marker=["ro","bp","ro","bp"]
for num,i in enumerate(marker):
    ax.plot(X[num,0],X[num,1],i,markersize=25)
ax.grid(ls='--')
ax.set_xlim(-0.25,1.25)
#初始化
w_0,b_0=[-1,-1],1
stop_sign="start"
result=[]
while stop_sign:
    m,_=X.shape
    for i in range(m):
        x=X[i,:]
        y=Y[i]
        temp=(w_0@x+b_0)*y
        if temp<=0:
            #更新参数设定
            w_0+=y*x
            b_0+=y
            a_0,a_1=w_0
            y_plot=-b_0[0]/a_1-a_0/a_1*x_plot
            #print(y_plot)
            #ax.cla()
            ax.plot(x_plot,y_plot,'--')
            ax.set_ylim(-0.5,1.2)
            ax.set_title(f"异或问题(XOR)(Time:{time.asctime()})",fontproperties="simhei",fontsize=12)
            #ax.legend()
            plt.pause(0.5)
            sign=str(i)
            print("误分类点：","x"+sign,", w：",w_0,"b：",b_0[0],"超平面：",str(w_0[0])+"*x^(1)+"+str(w_0[1])+"*x^(2)+"+str(b_0[0]))
            break
    else:
        stop_sign=""
    #plt.show()

---

参考：

• 李航的《统计学习方法》
• python绘制动图