Sklearn学习笔记:数据预处理
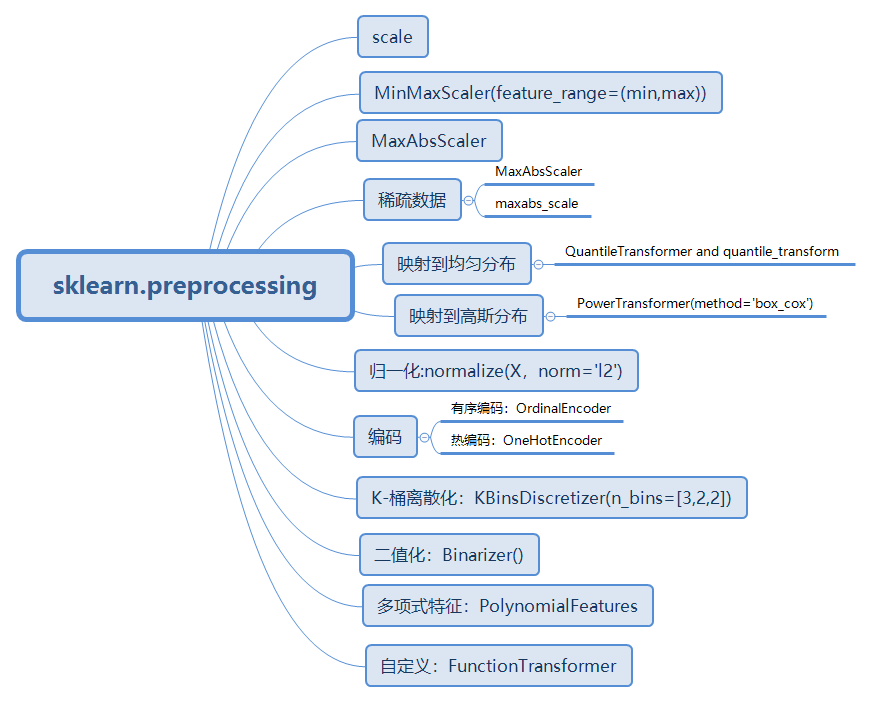
笔记:Preprocessing data — scikit-learn 0.22.2 documentation
标准化
from sklearn import preprocessing
import numpy as np
X_train=np.array([[1.,-1.,2.],
[1.,0.,0.],
[0.,1.0,-1.]])
help(preprocessing.scale)
scale(X, axis=0, with_mean=True, with_std=True, copy=True)
axis=0:默认是按照每一个特征(即按照列)进行标准化;
axis=1:则为行,按照样本进本进行标准化
X_scaled=preprocessing.scale(X_train)
X_scaled
array([[ 0.70710678, -1.22474487, 1.33630621],
[ 0.70710678, 0. , -0.26726124],
[-1.41421356, 1.22474487, -1.06904497]])
X_scaled.mean(axis=0)
array([7.40148683e-17, 0.00000000e+00, 0.00000000e+00])
X_scaled.std(axis=0)
array([1., 1., 1.])
#与之类似的是StandarScaler()
scaler=preprocessing.StandardScaler().fit(X_train)
scaler.mean_
array([0.66666667, 0. , 0.33333333])
#标准差
scaler.scale_
#等价于X_train.std(axis=0)
array([0.47140452, 0.81649658, 1.24721913])
scaler.transform(X_train)
array([[ 0.70710678, -1.22474487, 1.33630621],
[ 0.70710678, 0. , -0.26726124],
[-1.41421356, 1.22474487, -1.06904497]])
#对新数据
X_test=[[-1.,1.,0.]]
scaler.transform(X_test)
array([[-3.53553391, 1.22474487, -0.26726124]])
数据缩放
help(preprocessing.MinMaxScaler):
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
preprocessing.MinMaxScaler(feature_range=(min,max),copy=True)
min_max_scaler=preprocessing.MinMaxScaler()
X_train_minmax=min_max_scaler.fit_transform(X_train)
X_train_minmax
array([[1. , 0. , 1. ],
[1. , 0.5 , 0.33333333],
[0. , 1. , 0. ]])
#对于新数据的处理
X_test=np.array([[-3.,-1.,4.]])
X_test_minmax=min_max_scaler.transform(X_test)
X_test_minmax
array([[-3. , 0. , 1.66666667]])
min_max_scaler.scale_
array([1. , 0.5 , 0.33333333])
min_max_scaler.min_
array([0. , 0.5 , 0.33333333])
help(preprocessing.MaxAbsScaler):
class MaxAbsScaler(sklearn.base.TransformerMixin, sklearn.base.BaseEstimator)
Scale each feature by its maximum absolute(最大值的绝对值) value.
max_abs_scaler=preprocessing.MaxAbsScaler()
X_train=np.array([[1.,-1.,-2.],
[2.,0.,0.],
[0.,1.,-1.]])
X_train_maxabs=max_abs_scaler.fit_transform(X_train)
X_train_maxabs
array([[ 0.5, -1. , -1. ],
[ 1. , 0. , 0. ],
[ 0. , 1. , -0.5]])
核心问题节选:
1.Now the question is, should you do any of these things to your data? The answer is, it depends.
Standardization of cases should be approached with caution because it discards information. If that information is irrelevant, then standardizing cases can be quite helpful. If that information is important, then standardizing cases can be disastrous.
案例标准化应谨慎处理,因为它会丢弃信息。如果该信息无关紧要,则标准化案例可能会很有帮助。如果这些信息很重要,那么标准化案例可能是灾难性的。
2.Should I standardize the input variables (column vectors)(我应该标准化输入变量(列向量)吗)?
Two of the most useful ways to standardize inputs are:
o Mean 0 and standard deviation 1
o Midrange 0 and range 2 (i.e., minimum -1 and maximum 1)
Note that statistics such as the mean and standard deviation are computed from the training data, not from the validation or test data. The validation and test data must be standardized using the statistics computed from the training data.
标准化输入的两种最有用的方法是:
o均值0和标准偏差1
o中档0和范围2(即最小值-1和最大值1)
注意,诸如均值和标准差之类的统计数据是根据训练数据而非验证数据或测试数据计算得出的。 验证和测试数据必须使用根据训练数据计算出的统计数据进行标准化。
"这主要取决于网络如何结合输入变量来计算到下一层(隐藏层或输出层)的净输入。 如果在RBF网络中通过距离函数(例如欧几里得距离)组合输入变量,则标准化输入至关重要。 输入的贡献将在很大程度上取决于其相对于其他输入的可变性。 如果一个输入的范围是0到1,而另一个输入的范围是0到1,000,000,则第二个输入将淹没第一个输入对距离的贡献。 因此,必须重新调整输入的比例,以使它们的可变性反映其重要性,或者至少与它们的重要性不成反比。 由于缺少更好的先验信息,通常将每个输入标准化为相同的范围或相同的标准偏差。 如果您知道某些输入比其他输入更重要,则可能有助于缩放输入,以使更重要的输入具有更大的方差和/或范围。"
"标准化目标变量通常比获得必需品更容易获得良好的初始权重。 但是,如果您有两个或多个目标变量,并且您的误差函数像通常的最小(均方)误差函数一样对比例敏感,则每个目标相对于其他目标的可变性都会影响网络学习该目标的能力。 如果一个目标的范围是0到1,而另一个目标的范围是0到1,000,000,则网络将花费大部分精力来学习第二个目标,而可能排除第一个目标。 因此,必须重新调整目标的大小,以使目标的可变性反映其重要性,或者至少与目标的重要性不成反比。 如果目标具有同等的重要性,则通常应将其标准化为相同的范围或相同的标准偏差。"
"如果您正在标准化目标以平衡其重要性,那么您是否应该标准化为均值0和标准偏差1,或使用相关的鲁棒估计量,如我应标准化输入变量(列向量)所述? 如果您要标准化目标以将值强制到输出激活函数的范围内,那么使用下限值和上限值而不是训练集中的最小值和最大值非常重要。"
3. Should I standardize the variables (column vectors) for unsupervised learning?
无监督学习最常用的方法包括各种矢量量化,Kohonen网络,Hebbian学习等,取决于欧几里得距离或标量积相似性度量。 因此,注意事项与在RBF网络中标准化输入相同-请参阅是否应标准化输入变量(列向量)? 以上。 特别是,如果一个输入具有较大的方差,而另一输入具有较小的方差,则后者对结果的影响很小或没有影响。
4. Should I standardize the input cases (row vectors)?
Whereas standardizing variables is usually beneficial, the effect of standardizing cases (row vectors) depends on the particular data. Cases are typically standardized only across the input variables, since including the target variable(s) in the standardization would make prediction impossible.
标准化变量通常是有益的,而标准化案例(行向量)的效果取决于特定数据。 案例通常仅跨输入变量进行标准化,因为在标准化中包含目标变量将使预测变得不可能。
有几种网络,例如简单的Kohonen网络,需要将输入案例标准化为通用的欧几里得长度。这是使用内积作为相似性度量的副作用。如果将网络修改为在欧几里得距离上运行,而不是在内部乘积上运行,则不再需要标准化输入条件。
案例标准化应谨慎处理,因为它会丢弃信息。如果该信息无关紧要,则标准化案例可能会很有帮助。如果这些信息很重要,那么标准化案例可能是灾难性的。必须在每个应用程序中仔细评估有关案例标准化的问题。没有适用于所有应用程序的经验法则。
如果案例之间存在无关性的变化,则可能需要对每个案例进行标准化。考虑以下常见情况:每个输入变量代表图像中的一个像素。如果图像的曝光不同,并且曝光与目标值无关,那么通常将有助于减去每个案例的平均值,以等于不同案例的曝光。如果图像的对比度变化,并且对比度与目标值无关,那么通常将有助于将每种情况除以其标准偏差,以等同于不同情况的对比度。给定足够的数据,NN可以学会忽略曝光和对比度。但是,如果您可以在训练网络之前删除多余的曝光和对比度信息,则训练将更容易,泛化效果更好。
再举一个例子,假设您想根据物种对植物标本进行分类,但是标本处于不同的生长阶段。您可以进行测量,例如茎长,叶长和叶宽。但是,标本的总体大小取决于年龄或生长条件,而不取决于物种。给定足够的数据,NN可以学会忽略样本的大小,而是通过形状对其进行分类。但是,如果您可以在训练网络之前删除多余的大小信息,则训练将更容易,并且泛化效果更好。植物示例中的尺寸对应于图像示例中的曝光。
如果输入数据是按间隔刻度测量的(有关
比例尺,请参阅“测量原理:常见问题”,网址为ftp://ftp.sas.com/pub/neural/measurement.html),您可以通过减去每个尺寸的整体尺寸来控制尺寸每个数据的大小写。例如,如果没有其他直接的尺寸度量可用,则可以减去输入矩阵每一行的平均值,从而生成以行为中心的输入矩阵。
如果数据是按比例尺测量的,则可以通过以下方式控制尺寸
将每个基准除以整体大小的度量。通常用总和或算术平均值除。但是,对于正比数据,几何平均值通常是比算术平均值更自然的尺寸度量。分析正比例缩放数据的对数可能也更有意义,在这种情况下,您可以在取对数后减去算术平均值。您还必须考虑测量尺寸。例如,如果您具有长度和重量的度量,则可能需要对长度度量求立方,或者取权重的立方根。
在具有比率级数据的NN应用中,通常除以
每行的欧几里得长度。如果数据为正,则除以
欧几里德长度的性质类似于除以和或算术平均值,因为前者将数据点投影到超球面上,而后者将点投影到超平面上。如果维数不太高,则超球面和超平面上的点的最终配置通常非常相似。如果数据包含负值,那么超球面和超平面可能会大相径庭。
————————————————————————————————————————————————————————————————
映射到均匀分布
help(preprocessing.QuantileTransformer)
class QuantileTransformer(sklearn.base.TransformerMixin, sklearn.base.BaseEstimator)
Transform features using quantiles information(使用分位数信息变换特征).
preprocessing.QuantileTransformer(n_quantiles=1000, output_distribution='uniform', ignore_implicit_zeros=False, subsample=100000, random_state=None, copy=True)[source]¶
Marginal distribution for the transformed data. The choices are ‘uniform’ (default) or ‘normal’.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
X,y=load_iris(return_X_y=True)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
quantile_transformer=preprocessing.QuantileTransformer(random_state=0)
X_train_trans=quantile_transformer.fit_transform(X_train)
X_test_trans=quantile_transformer.transform(X_test)
np.percentile(X_train[:,0],[0,25,50,75,100])
array([4.3, 5.1, 5.8, 6.5, 7.9])
np.percentile(X_train_trans[:,0],[0,25,50,75,100])
array([0. , 0.23873874, 0.50900901, 0.74324324, 1. ])
#### 映射到高斯分布
help(preprocessing.PowerTransformer)
class PowerTransformer(sklearn.base.TransformerMixin, sklearn.base.BaseEstimator)
| Apply a power transform featurewise to make data more Gaussian-like.
Parameters
| method : str, (default='yeo-johnson')
| The power transform method. Available methods are:
|
| - 'yeo-johnson' [1]_, works with positive and negative values
| - 'box-cox' [2]_, only works with strictly positive values
pt=preprocessing.PowerTransformer(method='box-cox',standardize=False)
X_lognormal=np.random.RandomState(616).lognormal(size=(3,3))
X_lognormal
array([[1.28331718, 1.18092228, 0.84160269],
[0.94293279, 1.60960836, 0.3879099 ],
[1.35235668, 0.21715673, 1.09977091]])
pt.fit_transform(X_lognormal)
array([[ 0.49024349, 0.17881995, -0.1563781 ],
[-0.05102892, 0.58863195, -0.57612414],
[ 0.69420009, -0.84857822, 0.10051454]])
归一化
help(preprocessing.normalize)
normalize(X, norm='l2', axis=1, copy=True, return_norm=False)
Scale input vectors individually to unit norm (vector length).
norm : 'l1', 'l2', or 'max', optional ('l2' by default)
The norm to use to normalize each non zero sample (or each non-zero feature if axis is 0).
axis : 0 or 1, optional (1 by default)
axis used to normalize the data along. If 1, independently normalize each sample, otherwise (if 0) normalize each feature.
X_train=np.array([[1.,-1.,-2.],
[2.,0.,0.],
[0.,1.,-1.]])
X_train_normalized=preprocessing.normalize(X_train,norm='l2')
X_train_normalized
array([[ 0.40824829, -0.40824829, -0.81649658],
[ 1. , 0. , 0. ],
[ 0. , 0.70710678, -0.70710678]])
#使用管道函数:sklearn.pipeline.Pipeline
normalizer=preprocessing.Normalizer().fit(X_train)
normalizer
Normalizer(copy=True, norm='l2')
normalizer.transform(X_train)
array([[ 0.40824829, -0.40824829, -0.81649658],
[ 1. , 0. , 0. ],
[ 0. , 0.70710678, -0.70710678]])
#### 编码
help(preprocessing.OrdinalEncoder):
class OrdinalEncoder(_BaseEncoder)
| Encode categorical features as an integer array.
| The input to this transformer should be an array-like of integers or strings, denoting the values taken on by categorical (discrete) features.
| The features are converted to ordinal integers. This results in a single column of integers (0 to n_categories - 1) per feature.
enc = preprocessing.OrdinalEncoder()
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
enc.fit(X)
OrdinalEncoder(categories='auto', dtype=<class 'numpy.float64'>)
enc.transform([['female', 'from US', 'uses Safari']])
array([[0., 1., 1.]])
genders = ['female', 'male']
locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
enc = preprocessing.OneHotEncoder(categories=[genders, locations, browsers])
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
enc.fit(X)
OneHotEncoder(categories=[['female', 'male'],
['from Africa', 'from Asia', 'from Europe',
'from US'],
['uses Chrome', 'uses Firefox', 'uses IE',
'uses Safari']],
drop=None, dtype=<class 'numpy.float64'>, handle_unknown='error',
sparse=True)
enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray()
#逆操作
enc.inverse_transform(np.array([[1., 0., 0., 1., 0., 0., 1., 0., 0., 0.]]))
array([['female', 'from Asia', 'uses Chrome']], dtype=object)
enc.categories_
[array(['female', 'male'], dtype=object),
array(['from Africa', 'from Asia', 'from Europe', 'from US'], dtype=object),
array(['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari'],
dtype=object)]
enc.get_feature_names()
array(['x0_female', 'x0_male', 'x1_from Africa', 'x1_from Asia',
'x1_from Europe', 'x1_from US', 'x2_uses Chrome',
'x2_uses Firefox', 'x2_uses IE', 'x2_uses Safari'], dtype=object)
#### K-bins离散化
help(preprocessing.KBinsDiscretizer):
class KBinsDiscretizer(sklearn.base.TransformerMixin,sklearn.base.BaseEstimator) Bin continuous data into intervals.
Parameters
n_bins : int or array-like, shape (n_features,) (default=5)
The number of bins to produce. Raises ValueError if n_bins < 2.
encode : {'onehot', 'onehot-dense', 'ordinal'}, (default='onehot')Method used to encode the transformed result.
onehot:Encode the transformed result with one-hot encoding and return a sparse matrix. Ignored features are always stacked to the right.
onehot-dense:Encode the transformed result with one-hot encoding and return a dense array. Ignored features are always stacked to the right.
ordinal:Return the bin identifier encoded as an integer value.
strategy : {'uniform', 'quantile', 'kmeans'}, (default='quantile')
Strategy used to define the widths of the bins.
X=np.array([[-3,5.,15],
[0.,6.,14],
[6.,3.,11]])
est=preprocessing.KBinsDiscretizer(n_bins=[3,2,2],encode='ordinal').fit(X)
#生成的箱是左闭右开
"""
特征1:[-3,-1)-->0;
[-1,2)-->1;
[2,6]-->3
"""
est.bin_edges_
array([array([-3., -1., 2., 6.]), array([3., 5., 6.]),
array([11., 14., 15.])], dtype=object)
est.transform(X)
array([[0., 1., 1.],
[1., 1., 1.],
[2., 0., 0.]])
help(preprocessing.Binarizer):二值编码(默认阈值为0)
class Binarizer(sklearn.base.TransformerMixin, sklearn.base.BaseEstimator)
| Binarize data (set feature values to 0 or 1) according to a threshold
| Values greater than the threshold map to 1, while values less than or equal to the threshold map to 0. With the default threshold of 0,
| only positive values map to 1.
| Binarization is a common operation on text count data where the analyst can decide to only consider the presence or absence of a
| feature rather than a quantified number of occurrences for instance.
| It can also be used as a pre-processing step for estimators that consider boolean random variables (e.g. modelled using the Bernoulli
| distribution in a Bayesian setting).
Parameters
| threshold : float, optional (0.0 by default)
| Feature values below or equal to this are replaced by 0, above it by 1.
| Threshold may not be less than 0 for operations on sparse matrices.
binarizer = preprocessing.Binarizer(threshold=5.5).fit(X) # fit does nothing
binarizer.transform(X)
array([[0., 0., 1.],
[0., 1., 1.],
[1., 0., 1.]])
#### 生成多项式特征
help(preprocessing.PolynomialFeatures)
class PolynomialFeatures(sklearn.base.TransformerMixin,sklearn.base.BaseEstimator)
| Generate polynomial and interaction features.
|
| Generate a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified degree.
| For example, if an input sample is two dimensional and of the form [a, b], the degree-2 polynomial features are [1, a, b, a^2, ab, b^2].
Parameters
degreeinteger:The degree of the polynomial features. Default = 2.
interaction_onlyboolean, default = False
If true, only interaction features are produced: features that are products of at most degree distinct input features (so not x[1] ** 2, x[0] * x[2] ** 3, etc.).
include_biasboolean:
If True (default), then include a bias column, the feature in which all polynomial powers are zero (i.e. a column of ones -acts as an intercept term in a linear model).
X=np.arange(6).reshape(3,2)
X
array([[0, 1],
[2, 3],
[4, 5]])
poly=preprocessing.PolynomialFeatures(2)
poly.fit_transform(X)
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])
poly1=preprocessing.PolynomialFeatures(1)
poly1.fit_transform(X)
array([[1., 0., 1.],
[1., 2., 3.],
[1., 4., 5.]])
#交互项设置
X=np.arange(9).reshape(3,3)
X
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
poly=preprocessing.PolynomialFeatures(degree=3,interaction_only=True)
poly.fit_transform(X)
#X的特征已经从(x1,x2,x3)到(1,x1,x2,x3,x1x2,x1x3,x2x3,x1x2x3)
array([[ 1., 0., 1., 2., 0., 0., 2., 0.],
[ 1., 3., 4., 5., 12., 15., 20., 60.],
[ 1., 6., 7., 8., 42., 48., 56., 336.]])
#### 自定义编码
help(preprocessing.FunctionTransformer)
transformer=preprocessing.FunctionTransformer(np.log1p,validate=True)
#np.log1p:在整个数组上逐个元素操作的函数,Calculates ``log(1 + x)``.。
X=np.array([[0,1],[2,3]])
transformer.transform(X)
array([[0. , 0.69314718],
[1.09861229, 1.38629436]])



 浙公网安备 33010602011771号
浙公网安备 33010602011771号