决策树(二):分类决策树
决策树基本知识概览

基于特征的数据集划分指标
指标定义
- 信息增益
划分数据集的大原则是将无序的数据变得更加有序。
定义1:将划分前后信息发生的变化称为信息增益,且信息增益最高的特征就是最好的(特征)选择。
定义2:符号x信息的定义:\(l(x)=-log_2 p(x)\),p(x)是选择该类的概率.
定义3:信息熵定义为信息的期望值。
假如符号x包含在多个类中,所以其期望:
\[H=-sum p(x_i)*log_2p(x_i)
\]
基于上述定义计算信息增益.假定离散属性(即特征)a由V个可能得取值,\(\{a^1,a^2,...,a^V\}\).使用a对样本集D进行划分,若每一个取值对应得数据集为\(D^v\),则可以计算出该属性得信息增益:
\[Gain(D,a)=H(D)-sum_1 ^V |D^v|/|D|H(D^v)
\]
著名的ID3算法以该准则来选择划分属性。
缺点:信息增益准则对可取值数目较多的属性有所偏好。
修正: 为了修正这种影响,产生了增益率指标。采用该修正规则的算法为C4.5.计算公式如下:

信息增益率准则对可取值数目较少的属性有所偏好。在C4.5算法中并不是直接选择增益率最大的候选划分属性,而是
使用了一个启发式策略:先从候选属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的。
- 基尼指数
基尼值:用来度量数据集D的纯度。计算公式如下:
![基尼值计算]()
Gini(D)反映了从数据集D中随机出去两个样本,其类别标记不一致的概率. 因此,Gini(D)越小,则数据集D的纯度越高
属性a的基尼指数定义为:

采用该指标的算法为CART算法。
简单应用
以《统计学习方法中》中的贷款数据为例.分别采用信息增益和基尼指数计算出第一个最优特征。
import pandas as pd
import math
DATA=pd.read_excel(r'F:\Python_processing\Python_Jupyter脚本集\机器学习\loan.xlsx')
DATA
| Age | Work | House | Loan | Class | |
|---|---|---|---|---|---|
| 0 | 青年 | 否 | 否 | 一般 | 否 |
| 1 | 青年 | 否 | 否 | 好 | 否 |
| 2 | 青年 | 是 | 否 | 好 | 是 |
| 3 | 青年 | 是 | 是 | 一般 | 是 |
| 4 | 青年 | 否 | 否 | 一般 | 否 |
| 5 | 中年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 好 | 否 |
| 7 | 中年 | 是 | 是 | 好 | 是 |
| 8 | 中年 | 否 | 是 | 非常好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 老年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 好 | 是 |
| 12 | 老年 | 是 | 否 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 非常好 | 是 |
| 14 | 老年 | 否 | 否 | 一般 | 否 |
#列名
column=DATA.columns
from sklearn.preprocessing import OneHotEncoder
one_hot=OneHotEncoder().fit(DATA)
one_hot.categories_
[array(['中年', '老年', '青年'], dtype=object),
array(['否', '是'], dtype=object),
array(['否', '是'], dtype=object),
array(['一般', '好', '非常好'], dtype=object),
array(['否', '是'], dtype=object)]
one_hot.get_feature_names()
array(['x0_中年', 'x0_老年', 'x0_青年', 'x1_否', 'x1_是', 'x2_否', 'x2_是', 'x3_一般',
'x3_好', 'x3_非常好', 'x4_否', 'x4_是'], dtype=object)
#开始构造新列名的前缀,即用列名替换x0,x1,x2,x3
new_columns_prefix=[]
for i in column:
temp=[i for j in range(len(set(DATA[i])))]
new_columns_prefix.extend(temp)
#构造后缀
new_columns_postfix=[i.split("_")[-1] for i in one_hot.get_feature_names()]
#新列名
new_columns=[i+'_'+j for i,j in zip(new_columns_prefix,new_columns_postfix)]
#编码后的数据
data=pd.DataFrame(one_hot.transform(DATA[column]).toarray(),columns=new_columns)
data_shape_m=data.shape[0]
data
| Age_中年 | Age_老年 | Age_青年 | Work_否 | Work_是 | House _否 | House _是 | Loan_一般 | Loan_好 | Loan_非常好 | Class_否 | Class_是 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 1 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 |
| 2 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| 3 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 |
| 4 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 5 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 6 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 |
| 7 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| 8 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 |
| 9 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 |
| 10 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 |
| 11 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| 12 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| 13 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 |
| 14 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 |
信息增益计算案例
#计算H_D
#为了方便将其定义成函数
def calEntropy(target_data):
"""
计算信息熵
target_data:为数据框
"""
data_counts=target_data.value_counts()
data_values=data_counts.values
res=sum([-i*math.log(i,2) for i in data_values/sum(data_values)])
return res
H_D=calEntropy(data['Class_是'])
###### 以下是函数calEntropy的分步展示
print(''.center(100,'='))
data[data['Age_中年']==1.0]
| Age_中年 | Age_老年 | Age_青年 | Work_否 | Work_是 | House _否 | House _是 | Loan_一般 | Loan_好 | Loan_非常好 | Class_否 | Class_是 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 6 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 |
| 7 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| 8 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 |
| 9 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 1.0 |
temp=data[data['Age_中年']==1.0]['Class_是'].value_counts()
temp
1.0 3
0.0 2
Name: Class_是, dtype: int64
temp_values=temp.values
temp_values
array([3, 2], dtype=int64)
temp_values/sum(temp_values)
array([0.6, 0.4])
#求信息熵
sum([-i*math.log(i,2) for i in temp_values/sum(temp_values)])
0.9709505944546686
#统计每一个特征划分后的信息熵
feature_entropy={}
print('开始结果统计'.center(30,'*'))
for col in new_columns[:-2]:
#特证名
fea_name=col.split('_')[0]
temp_data=data[data[col]==1.0]['Class_是']
entropy=calEntropy(temp_data)*temp_data.shape[0]/data_shape_m
feature_entropy[fea_name]=feature_entropy.get(fea_name,0)+entropy
print("特征属性:%5.6s, 划分后的信息熵:%10.6f"%(col,entropy))
print('统计结束'.center(30,'*'))
************开始结果统计************
特征属性:Age_中年, 划分后的信息熵: 0.323650
特征属性:Age_老年, 划分后的信息熵: 0.240643
特征属性:Age_青年, 划分后的信息熵: 0.323650
特征属性:Work_否, 划分后的信息熵: 0.647300
特征属性:Work_是, 划分后的信息熵: 0.000000
特征属性:House , 划分后的信息熵: 0.550978
特征属性:House , 划分后的信息熵: 0.000000
特征属性:Loan_一, 划分后的信息熵: 0.240643
特征属性:Loan_好, 划分后的信息熵: 0.367318
特征属性:Loan_非, 划分后的信息熵: 0.000000
*************统计结束*************
print("划分后信息熵统计结果:\n",feature_entropy)
feature_gain=dict([(i[0],H_D-i[1]) for i in feature_entropy.items()])
print("信息增益:\n",feature_gain)
feature_gain_values=feature_gain.values()
print(''.center(100,'='))
print("信息增益最大的特征是:%s"%([i[0] for i in feature_gain.items() if i[1]==max(feature_gain_values)][0]))
print(''.center(100,'='))
划分后信息熵统计结果:
{'Age': 0.8879430945988998, 'Work': 0.6473003963031124, 'House ': 0.5509775004326938, 'Loan': 0.6079610319175832}
信息增益:
{'Age': 0.08300749985576883, 'Work': 0.32365019815155616, 'House ': 0.4199730940219748, 'Loan': 0.36298956253708536}
====================================================================================================
信息增益最大的特征是:House
====================================================================================================
基尼指数计算案例
def calGiniValue(target_data):
"""
@params: 计算基尼值
"""
data_counts=target_data.value_counts()
data_values=data_counts.values
res=1-sum([(i/sum(data_values))**2 for i in data_values])
return res
#统计每一个特征的基尼指数
feature_gini={}
print('开始结果统计'.center(30,'*'))
for col in new_columns[:-2]:
#特证名
fea_name=col.split('_')[0]
temp_data=data[data[col]==1.0]['Class_是']
gini=calGiniValue(temp_data)*temp_data.shape[0]/data_shape_m
#print(gini)
feature_gini[fea_name]=feature_gini.get(fea_name,0)+gini
print("特征属性:%5.6s, 对应的基尼指数:%10.6f"%(col,gini))
print('统计结束'.center(30,'*'))
************开始结果统计************
特征属性:Age_中年, 对应的基尼指数: 0.160000
特征属性:Age_老年, 对应的基尼指数: 0.106667
特征属性:Age_青年, 对应的基尼指数: 0.160000
特征属性:Work_否, 对应的基尼指数: 0.320000
特征属性:Work_是, 对应的基尼指数: 0.000000
特征属性:House , 对应的基尼指数: 0.266667
特征属性:House , 对应的基尼指数: 0.000000
特征属性:Loan_一, 对应的基尼指数: 0.106667
特征属性:Loan_好, 对应的基尼指数: 0.177778
特征属性:Loan_非, 对应的基尼指数: 0.000000
*************统计结束*************
print("基尼指数:\n",feature_gini)
feature_gini_values=feature_gini.values()
print(''.center(100,'='))
print("基尼指数的特征是:%s"%([i[0] for i in feature_gini.items() if i[1]==min(feature_gini_values)][0]))
print(''.center(100,'='))
基尼指数:
{'Age': 0.42666666666666664, 'Work': 0.32, 'House ': 0.26666666666666666, 'Loan': 0.2844444444444444}
====================================================================================================
基尼指数的特征是:House
====================================================================================================
利用递归构建分类决策树
算法过程
- 以信息增益为例,将上述案例计算过程封装成函数
entropyMethod。
def entropyMethod(data):
"""
将上述基于信息增益确定特征的方法封装成函数
@params:data:为了方便这里的data是已经one_hot编码后的数据
"""
data_columns=data.columns
#统计每一个特征划分后的信息熵
feature_entropy={}
print('特征统计'.center(30,'*'))
each_feature_entropy={}
for col in data_columns[:-2]:
#特证名
fea_name=col.split('_')[0]
temp_data=data[data[col]==1.0]['Class_是']
entropy=calEntropy(temp_data)*temp_data.shape[0]/data_shape_m
each_feature_entropy[col]=entropy
feature_entropy[fea_name]=feature_entropy.get(fea_name,0)+entropy
#print("特征属性:%10.10s, 划分后的信息熵:%10.6f"%(col,entropy))
print('统计结束'.center(30,'*'))
print("划分后信息熵统计结果:\n",feature_entropy)
feature_gain=dict([(i[0],H_D-i[1]) for i in feature_entropy.items()])
print("信息增益:\n",feature_gain)
feature_gain_values=feature_gain.values()
print(''.center(100,'='))
feature_name=[i[0] for i in feature_gain.items() if i[1]==max(feature_gain_values)][0]
#print("信息增益最大的特征是:%s"%(feature_name))
return feature_name,each_feature_entropy
- 在最优特征确定的情况下,确定下一步的分支结点(若存在多个,取一个即可),并修改数据集
data(方便递归).
def chooseNextNode(pre_node,pre_node_entropy):
"""
这个函数用来筛选下一个分支节点
@params:pre_node:是前一步确定的最优特征
@params:pre_node_entropy前一步每一个特征节点的熵值
"""
temp_entropy=dict([i for i in pre_node_entropy.items() if i[0].split('_')[0]==pre_node])
#print("temp_entropy:\n",temp_entropy)
temp_entropy_values=temp_entropy.values()
#若存在多个节点的熵值最大,取第一个
next_nodename=[i[0] for i in temp_entropy.items() if i[1]==max(temp_entropy_values)][0]
print("\t\t -->*-->*-->|||确定的下一个特征节点是:%s"%next_nodename)
return next_nodename
- 最后将其封装。
def decisionClassifier(data,raw_features):
"""
利用递归实现分类决策树
@params:为了方便这里的data是已经one_hot编码后的数据
@params:raw_feature:未编码的特征,type=list
以信息增益为例
"""
print("开始分类决策树建模:".center(100,'='))
while len(raw_features)>0:
print(''.center(120,'*'))
feature_name,each_feature_entropy=entropyMethod(data)
#选择目标分支
next_nodename=chooseNextNode(feature_name,each_feature_entropy)
#修改data
#剔除上一个特征
raw_features.remove(feature_name)
temp_columns=[i for i in data.columns if i.split('_')[0]!=feature_name]
#筛选后的数据集
data=data[data[next_nodename]==1.0][temp_columns]
#print(data.head(2))
print(''.center(120,'*'))
print("分类决策树建模完成!".center(100,'='))
运行结果
- 调用
raw_features=[i for i in DATA.columns[:-1]]
decisionClassifier(data,raw_features)
- 结果
=============================================开始分类决策树建模:=============================================
************************************************************************************************************************
*************特征统计*************
*************统计结束*************
划分后信息熵统计结果:
{'Age': 0.8879430945988998, 'Work': 0.6473003963031124, 'House': 0.5509775004326938, 'Loan': 0.6079610319175832}
信息增益:
{'Age': 0.08300749985576883, 'Work': 0.32365019815155616, 'House': 0.4199730940219748, 'Loan': 0.36298956253708536}
====================================================================================================
-->*-->*-->|||确定的下一个特征节点是:House_否
************************************************************************************************************************
************************************************************************************************************************
*************特征统计*************
*************统计结束*************
划分后信息熵统计结果:
{'Age': 0.4, 'Work': 0.0, 'Loan': 0.26666666666666666}
信息增益:
{'Age': 0.5709505944546686, 'Work': 0.9709505944546686, 'Loan': 0.704283927788002}
====================================================================================================
-->*-->*-->|||确定的下一个特征节点是:Work_否
************************************************************************************************************************
************************************************************************************************************************
*************特征统计*************
*************统计结束*************
划分后信息熵统计结果:
{'Age': 0.0, 'Loan': 0.0}
信息增益:
{'Age': 0.9709505944546686, 'Loan': 0.9709505944546686}
====================================================================================================
-->*-->*-->|||确定的下一个特征节点是:Age_中年
************************************************************************************************************************
************************************************************************************************************************
*************特征统计*************
*************统计结束*************
划分后信息熵统计结果:
{'Loan': 0.0}
信息增益:
{'Loan': 0.9709505944546686}
====================================================================================================
-->*-->*-->|||确定的下一个特征节点是:Loan_一般
************************************************************************************************************************
=============================================分类决策树建模完成!=============================================
调用Sklearn包及可视化
- 决策树可视化中需要 graphviz 安装
注意:Graphviz配置路径有时候在环境变量中已经配置过,仍然没有生效,可以使用下述代码:
(忘了原博客的链接,罪过!!!!)
import os
os.environ["PATH"] += os.pathsep + 'C:/Program Files (x86)/Graphviz2.38/bin/'
from sklearn import tree
from sklearn.datasets import load_iris
from IPython.display import Image
import pydotplus
# 使用iris数据
iris=load_iris()
# 生成决策分类树实例
clf = tree.DecisionTreeClassifier()
# 拟合iris数据
clf = clf.fit(iris.data, iris.target)
# 预测类别
clf.predict(iris.data[:1, :])
# 分别预测属于所有类别的可能性
clf.predict_proba(iris.data[:1, :])
# 可视化决策树
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True, rounded=True,
special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data)
# 显示图片
Image(graph.create_png())
参考文献:
1.周志华.《机器学习》,2016版.
2.李航.《统计学习方法》.
3.机器学习实战


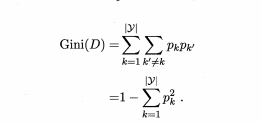

 浙公网安备 33010602011771号
浙公网安备 33010602011771号