《Python深度学习》笔记(二):Keras基础
keras常用数据集
常用数据集 Datasets - Keras 中文文档
鉴于官网下载较慢,个人将下载好的数据已打包(见链接 提取码:8j6x),下载后替换C:\Users\Administrator\.keras中的datasets文件夹即可。
基本概念
-
在机器学习中,分类问题中的某个列别叫做类(class).数据点叫做样本(sample).某一个样本对应的类叫做标签(label)。
-
张量:它是一个数据容器。是矩阵像任意维度的推广,张量的维度(dimension)通常叫作轴(axis).
-
标量(0D张量)
-
仅包含一个数字的张量叫作标量(scaler,也叫做标量张量、零维张量、0D张量)
-
张量的个数也叫做阶(rank)
-
标量张量有0个轴。
-
-
向量(1D张量)
- 数字组成的数组叫作向量或一维张量。以为张量只有一个轴。
x.ndim
- 数字组成的数组叫作向量或一维张量。以为张量只有一个轴。
import numpy as np
x=np.array([12,3,6,14,7])
x.ndim
1
上述向量有5个元素,所以被称为5D向量。
5D向量和5D张量的区别:
5D向量只有一个轴,沿着轴有五个维度;5D张量有5个轴(沿着每个轴可能有人一个维度)
维度:表示沿着某个轴上的元素个数
矩阵
- 向量组成的数组叫作矩阵或二维张量,两个轴(行和列)
- 第一个轴上的元素叫作行(row),第二个轴上的元素叫作列。
3D张量与更高维张量
- 将多个矩阵组合成的一个新的数组,可以得到一个3D张量。
张量的关键属性:
- 轴的个数(阶),张量的ndim.
- 形状 shape
- 数据类型(Python库中通常叫作dtype)
数据批量:
- 通常来说,深度学习中所有数据张量的第一个轴(0轴,因为索引从0开始)都是样本轴(sample axis,有时也叫样本维度)。
- 如:
batch=train_images[:128] batch=train_images[128:256] 对于这种批量张量,第一个轴(0轴)叫作批量轴(batch axis)或批量维度(batch dimension)
常见的数据张量:
- 向量数据:2D张量,形状为(samples(样本轴),features(特征轴));
- 时间序列数据或序列数据:3D张量,形状(samples,timesteps,features);
- 图像:4D张量,形状为(samples,height,width,channels)
或(samples,channels,height,width); - 视频:5D张量,形状为:(samples,frames,height,width,channels)或
(samples,frames,channels,height,width).
逐元素计算
- relu运算和加法
广播:
较小的张量会被广播(broadcast),以匹配较大张量的形状
步骤:
- 向较小的张量添加轴(叫作广播轴),使其ndim与较大的张量相同。
- 将较小的张量沿着新轴重复,使其形状与较大的张量相同。
张量点积
- 点积运算,也叫张量积(tensor product,不要与逐元素的乘积弄混)
- 在numpy、Keras、tensorflow中都是适用
*实现逐元素乘积。 - np.dot()实现点积运算。
矩阵点积运算的条件:第一个矩阵的列(1轴的维度)数和第二个矩阵的行数(0轴的维度)相同
Keras简介
一个Python深度学习框架。
重要特性:
- 相同的代码可以在CPU或GPU上无缝转换运行;
- 具有用户友好的API,便于快速开发深度学习模型的原型;
- 内置支持卷积网络(用于计算机视觉)、循环网络(用于时序处理)以及二者的任意组合;
- 支持任意网络架构:
多输入或多输出模型、层共享、模型共享等。
Keras 是一个模型级( model-level)的库,为开发深度学习模型提供了高层次的构建模块。它不处理张量操作、求微分等低层次的运算。相反,它依赖于一个专门的、高度优化的张量库来完成这些运算,这个张量库就是 Keras 的后端引擎( backend engine)。 Keras 没有选择单个张量库并将 Keras 实现与这个库绑定,而是以模块化的方式处理这个问题。因此,几个不同的后端引擎都可以无缝嵌入到 Keras 中。目前, Keras 有三个后端实现: TensorFlow 后端、Theano 后端和微软认知工具包( CNTK, Microsoft cognitive toolkit)后端。未来 Keras 可能会扩展到支持更多的深度学习引擎。
Keras工作流程:
- 定义训练数据:输入张量和目标张量;
- 定义层组成的网络(或模型),将输入映射到目标;
- 配置学习过程:选择损失函数、优化器和需要监控的指标
- 调用模型的fit方法在训练数据上进行迭代。
搭建流程案例:
- 1.深度学习的基础组件
from keras import models
from keras import layers
model=models.Sequential()
model.add(layers.Dense(32,input_shape=(784,)))
#第二层未指定形状,将会自动推断
model.add(layers.Dense(32))
- 2.模型:层构成的网络
深度学习模型是层构成的有向无环图。常见的拓扑结构:
- 双分支(two-branch)网络
- 多头网络
- Inception模块
- 3. 损失函数与优化器:配置学习过程的关键
- 损失函数(目标函数):在训练过程中需要将其最小化,它能够衡量当前任务是否已成功完成。
- 优化器——决定如何基于损失函数对网络进行更新,它执行的是随机梯度下降(SGD的某一个变体。
案例1:电影评论分类:二分类问题.
数据集:IMDB.它包含来自互联网电影数据库( IMDB)的 50 000 条严重两极分化的评论。数据集被分为用于训练的 25 000 条评论与用于测试的 25 000 条评论,训练集和测试集都包含 50% 的正面评论和 50% 的负面评论.
#加载数据集
from keras.datasets import imdb
#仅保留训练数据中前10000个最常出现的单词
(train_data,train_labels),(test_data,test_labels)=imdb.load_data('imdb.npz',num_words=10000)
print(train_data[0])
#每一条评论由单词对应的索引组成
[1, 14, 22, 16, 43, 530, 973, 1622, 1385, 65, 458, 4468, 66, 3941, 4, 173, 36, 256, 5, 25, 100, 43, 838, 112, 50, 670, 2, 9, 35, 480, 284, 5, 150, 4, 172, 112, 167, 2, 336, 385, 39, 4, 172, 4536, 1111, 17, 546, 38, 13, 447, 4, 192, 50, 16, 6, 147, 2025, 19, 14, 22, 4, 1920, 4613, 469, 4, 22, 71, 87, 12, 16, 43, 530, 38, 76, 15, 13, 1247, 4, 22, 17, 515, 17, 12, 16, 626, 18, 2, 5, 62, 386, 12, 8, 316, 8, 106, 5, 4, 2223, 5244, 16, 480, 66, 3785, 33, 4, 130, 12, 16, 38, 619, 5, 25, 124, 51, 36, 135, 48, 25, 1415, 33, 6, 22, 12, 215, 28, 77, 52, 5, 14, 407, 16, 82, 2, 8, 4, 107, 117, 5952, 15, 256, 4, 2, 7, 3766, 5, 723, 36, 71, 43, 530, 476, 26, 400, 317, 46, 7, 4, 2, 1029, 13, 104, 88, 4, 381, 15, 297, 98, 32, 2071, 56, 26, 141, 6, 194, 7486, 18, 4, 226, 22, 21, 134, 476, 26, 480, 5, 144, 30, 5535, 18, 51, 36, 28, 224, 92, 25, 104, 4, 226, 65, 16, 38, 1334, 88, 12, 16, 283, 5, 16, 4472, 113, 103, 32, 15, 16, 5345, 19, 178, 32]
print(train_labels[0])
#0表示负面(negative),1代表正面(postive)
1
#word_index是一个将单词映射成整数索引的字典
#get_word_index()数据集可以单独下载保存到根目录
word_index=imdb.get_word_index()
reverse_word_index=dict(
[(value,key) for (key,value) in word_index.items()]
)
decoded_review=" ".join(
[reverse_word_index.get(i-3,"?") for i in train_data[0]]
)
#
print(decoded_review)
? this film was just brilliant casting location scenery story direction everyone's really suited the part they played and you could just imagine being there robert ? is an amazing actor and now the same being director ? father came from the same scottish island as myself so i loved the fact there was a real connection with this film the witty remarks throughout the film were great it was just brilliant so much that i bought the film as soon as it was released for ? and would recommend it to everyone to watch and the fly fishing was amazing really cried at the end it was so sad and you know what they say if you cry at a film it must have been good and this definitely was also ? to the two little boy's that played the ? of norman and paul they were just brilliant children are often left out of the ? list i think because the stars that play them all grown up are such a big profile for the whole film but these children are amazing and should be praised for what they have done don't you think the whole story was so lovely because it was true and was someone's life after all that was shared with us all
注意,索引减去了 3,因为 0、 1、 2是为“padding”(填充)、“start of sequence”(序列开始)、“unknown”(未知词)分别保留的索引
#准备数据
def vectorize_sequences(sequences,dimension=10000):
results=np.zeros((len(sequences),dimension))
#one_hot编码
for i,sequence in enumerate(sequences):
#指定索引为1
results[i,sequence]=1.
return results
将列表转换成张量。转换方法有以下两种:
- 填充列表,使其具有相同的长度,再将列表转换成形状为(samples,word_indices)的整数张量,然后网络第一层适用能处理这种整数张量的层(即Embedding层);
- 对列表进行one-hot编码
#数据向量化
x_train=vectorize_sequences(train_data)
x_test=vectorize_sequences(test_data)
x_train[0]
array([0., 1., 1., ..., 0., 0., 0.])
#标签向量化
y_train=np.asarray(train_labels).astype('float32')
y_test=np.asanyarray(test_labels).astype('float32')
print(y_train)
[1. 0. 0. ... 0. 1. 0.]
# 构建网络
# 每个带有 relu 激活的 Dense 层都实现了下列张量运算:output = relu(dot(W, input) + b)
对于这种 Dense 层的堆叠,你需要确定以下两个关键架构:
- 网络有多少层;
- 每层有多少个隐藏单元。
本节的构建策略:
- 两个中间层,每层16个隐藏单元;
- 第三层输出一个标量,预测当前评论的结果
#模型定义
from keras import models
from keras import layers
model=models.Sequential()
model.add(layers.Dense(16,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(16,activation='relu'))
model.add(layers.Dense(1,activation='sigmoid'))
什么是激活函数?为什么要使用激活函数?
如果没有 relu 等激活函数(也叫非线性), Dense 层将只包含两个线性运算——点积和加法:
output = dot(W, input) + b
这样 Dense 层就只能学习输入数据的线性变换(仿射变换):该层的假设空间是从输入数据到 16 位空间所有可能的线性变换集合。这种假设空间非常有限,无法利用多个表示层的优势,因为多个线性层堆叠实现的仍是线性运算,添加层数并不会扩展假设空间。为了得到更丰富的假设空间,从而充分利用多层表示的优势,你需要添加非线性或激活函数。 relu 是深度学习中最常用的激活函数,但还有许多其他函数可选,它们都有类似的奇怪名称,比如 prelu、 elu 等。
#损失函数和优化器
#1. 编译模型
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy']
)
注:
上述代码将优化器、损失函数和指标作为字符串传入,这是因为 rmsprop、 binary_crossentropy 和 accuracy 都是 Keras 内置的一部分。有时你可能希望配置自定义优化器的参数,或者传入自定义的损失函数或指标函数。前者可通过向 optimizer 参数传入一个优化器类实例来实现;后者可通过向 loss 和 metrics 参数传入函数对象来实现,如下所示。
#配置优化器
from keras import optimizers
from keras import metrics
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss='binary_crossentropy',
metrics=[metrics.binary_accuracy]
)
#留出验证集
x_val=x_train[:10000]
partial_x_train=x_train[10000:]
y_val=y_train[:10000]
partial_y_train=y_train[10000:]
#训练模型
#训练20个轮次
#使用512个样本组成小批量
history=model.fit(
partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val,y_val)
)
Train on 15000 samples, validate on 10000 samples
Epoch 1/20
15000/15000 [==============================] - 10s 692us/step - loss: 0.5350 - binary_accuracy: 0.7935 - val_loss: 0.4228 - val_binary_accuracy: 0.8566
Epoch 2/20
15000/15000 [==============================] - 7s 449us/step - loss: 0.3324 - binary_accuracy: 0.9013 - val_loss: 0.3218 - val_binary_accuracy: 0.8852
Epoch 3/20
15000/15000 [==============================] - 5s 335us/step - loss: 0.2418 - binary_accuracy: 0.9261 - val_loss: 0.2933 - val_binary_accuracy: 0.8861
Epoch 4/20
15000/15000 [==============================] - 5s 314us/step - loss: 0.1931 - binary_accuracy: 0.9385 - val_loss: 0.2746 - val_binary_accuracy: 0.8912
Epoch 5/20
15000/15000 [==============================] - 5s 308us/step - loss: 0.1587 - binary_accuracy: 0.9505 - val_loss: 0.2757 - val_binary_accuracy: 0.8897
Epoch 6/20
15000/15000 [==============================] - 5s 320us/step - loss: 0.1308 - binary_accuracy: 0.9597 - val_loss: 0.2837 - val_binary_accuracy: 0.8864
Epoch 7/20
15000/15000 [==============================] - 5s 340us/step - loss: 0.1110 - binary_accuracy: 0.9661 - val_loss: 0.2984 - val_binary_accuracy: 0.8849
Epoch 8/20
15000/15000 [==============================] - 5s 333us/step - loss: 0.0908 - binary_accuracy: 0.9733 - val_loss: 0.3157 - val_binary_accuracy: 0.8849
Epoch 9/20
15000/15000 [==============================] - 5s 332us/step - loss: 0.0754 - binary_accuracy: 0.9790 - val_loss: 0.3344 - val_binary_accuracy: 0.8809
Epoch 10/20
15000/15000 [==============================] - 5s 326us/step - loss: 0.0638 - binary_accuracy: 0.9836 - val_loss: 0.3696 - val_binary_accuracy: 0.8777
Epoch 11/20
15000/15000 [==============================] - 5s 344us/step - loss: 0.0510 - binary_accuracy: 0.9877 - val_loss: 0.3839 - val_binary_accuracy: 0.8770
Epoch 12/20
15000/15000 [==============================] - 5s 300us/step - loss: 0.0424 - binary_accuracy: 0.9907 - val_loss: 0.4301 - val_binary_accuracy: 0.8704
Epoch 13/20
15000/15000 [==============================] - 5s 314us/step - loss: 0.0362 - binary_accuracy: 0.9919 - val_loss: 0.4360 - val_binary_accuracy: 0.8746
Epoch 14/20
15000/15000 [==============================] - 5s 307us/step - loss: 0.0304 - binary_accuracy: 0.9936 - val_loss: 0.5087 - val_binary_accuracy: 0.8675
Epoch 15/20
15000/15000 [==============================] - 5s 313us/step - loss: 0.0212 - binary_accuracy: 0.9971 - val_loss: 0.4931 - val_binary_accuracy: 0.8710
Epoch 16/20
15000/15000 [==============================] - 5s 340us/step - loss: 0.0191 - binary_accuracy: 0.9969 - val_loss: 0.5738 - val_binary_accuracy: 0.8661
Epoch 17/20
15000/15000 [==============================] - 5s 344us/step - loss: 0.0138 - binary_accuracy: 0.9987 - val_loss: 0.5637 - val_binary_accuracy: 0.8697
Epoch 18/20
15000/15000 [==============================] - 6s 395us/step - loss: 0.0129 - binary_accuracy: 0.9983 - val_loss: 0.5944 - val_binary_accuracy: 0.8665
Epoch 19/20
15000/15000 [==============================] - 5s 357us/step - loss: 0.0075 - binary_accuracy: 0.9996 - val_loss: 0.6259 - val_binary_accuracy: 0.8671
Epoch 20/20
15000/15000 [==============================] - 5s 301us/step - loss: 0.0077 - binary_accuracy: 0.9991 - val_loss: 0.6556 - val_binary_accuracy: 0.8670
history
注意,调用 model.fit() 返回了一个 History 对象。这个对象有一个成员 history,它
是一个字典,包含训练过程中的所有数据。
history_dict=history.history
history_dict.keys()
dict_keys(['val_loss', 'val_binary_accuracy', 'loss', 'binary_accuracy'])
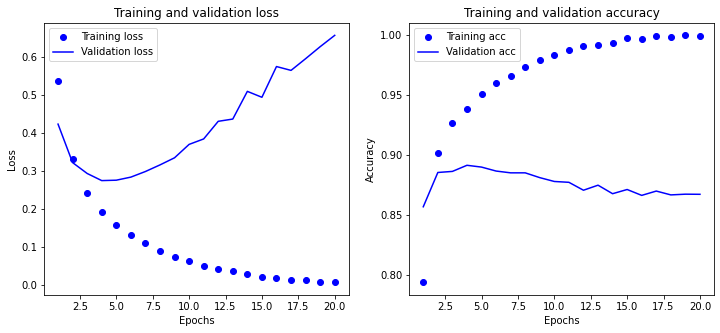
#绘制训练损失和验证损失
import matplotlib.pyplot as plt
loss_values=history_dict['loss']
val_loss_values=history_dict['val_loss']
epochs=range(1,len(loss_values)+1)
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(12,5))
Axes=axes.flatten()
#绘制训练损失和验证损失
Axes[0].plot(epochs,loss_values,'bo',label='Training loss')
Axes[0].plot(epochs,val_loss_values,'b',label='Validation loss')
Axes[0].set_title('Training and validation loss')
Axes[0].set_xlabel('Epochs')
Axes[0].set_ylabel('Loss')
Axes[0].legend()
#训练训练精度和验证精度
acc=history_dict['binary_accuracy']
val_acc=history_dict['val_binary_accuracy']
Axes[1].plot(epochs,acc,'bo',label='Training acc')
Axes[1].plot(epochs,val_acc,'b',label='Validation acc')
Axes[1].set_title('Training and validation accuracy')
Axes[1].set_xlabel('Epochs')
Axes[1].set_ylabel('Accuracy')
Axes[1].legend()
plt.show()
#重新训练一个新的网络,训练4轮
model=models.Sequential()
model.add(layers.Dense(16,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(16,activation='relu'))
model.add(layers.Dense(1,activation='sigmoid'))
model.compile(
optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy']
)
model.fit(x_train,y_train,epochs=4,batch_size=512)
results=model.evaluate(x_test,y_test)
Epoch 1/4
25000/25000 [==============================] - 6s 252us/step - loss: 0.4470 - acc: 0.8242
Epoch 2/4
25000/25000 [==============================] - 6s 224us/step - loss: 0.2557 - acc: 0.9103
Epoch 3/4
25000/25000 [==============================] - 6s 253us/step - loss: 0.1969 - acc: 0.9303
Epoch 4/4
25000/25000 [==============================] - 6s 233us/step - loss: 0.1645 - acc: 0.9422
25000/25000 [==============================] - 24s 955us/step
# 使用训练好的网络在新数据上生成预测结果
model.predict(x_test)
array([[0.29281223],
[0.99967945],
[0.93715465],
...,
[0.16654661],
[0.15739296],
[0.7685658 ]], dtype=float32)
小结
- 通常需要对原始数据进行大量预处理,以便将其转换为张量输入到神经网络中。单词序列可以编码为二进制向量,但也有其他编码方式。
- 带有 relu 激活的 Dense 层堆叠,可以解决很多种问题(包括情感分类),你可能会经常用到这种模型。
- 对于二分类问题(两个输出类别),网络的最后一层应该是只有一个单元并使用 sigmoid激活的 Dense 层,网络输出应该是 0~1 范围内的标量,表示概率值。
- 对于二分类问题的 sigmoid 标量输出,你应该使用 binary_crossentropy 损失函数。
- 无论你的问题是什么, rmsprop 优化器通常都是足够好的选择。这一点你无须担心。
- 随着神经网络在训练数据上的表现越来越好,模型最终会过拟合,并在前所未见的数据上得到越来越差的结果。一定要一直监控模型在训练集之外的数据上的性能。
案例2:新闻分类:多分类问题
-
任务:本节你会构建一个网络,将路透社新闻划分为 46 个互斥的主题。因为有多个类别,所以这是多分类( multiclass classification)问题的一个例子。因为每个数据点只能划分到一个类别,所以更具体地说,这是单标签、多分类( single-label, multiclass classification)问题的一个例子。如果每个数据点可以划分到多个类别(主题),那它就是一个多标签、多分类( multilabel,multiclass classification)问题。
-
数据集:reuters
本节使用路透社数据集,它包含许多短新闻及其对应的主题,由路透社在 1986 年发布。它是一个简单的、广泛使用的文本分类数据集。它包括 46 个不同的主题:某些主题的样本更多,但训练集中每个主题都有至少 10 个样本。
#加载数据
from keras.datasets import reuters
(train_data,train_labels),(test_data,test_labels)=reuters.load_data(num_words=10000)
print(train_data.shape,test_data.shape)
(8982,) (2246,)
#将索引解码为新闻文本
word_index=reuters.get_word_index()
reverse_word_index=dict(
[(value,key) for (key,value) in word_index.items()]
)
decoded_review=" ".join(
[reverse_word_index.get(i-3,"?") for i in train_data[0]]
)
#
print(decoded_review)
? ? ? said as a result of its december acquisition of space co it expects earnings per share in 1987 of 1 15 to 1 30 dlrs per share up from 70 cts in 1986 the company said pretax net should rise to nine to 10 mln dlrs from six mln dlrs in 1986 and rental operation revenues to 19 to 22 mln dlrs from 12 5 mln dlrs it said cash flow per share this year should be 2 50 to three dlrs reuter 3
#编码数据
#调用前面的方法向量化
x_train=vectorize_sequences(train_data)
x_test=vectorize_sequences(test_data)
#将标签向量化有两种方法:你可以将标签列表转换为整数张量,或者使用 one-hot 编码。
#one-hot 编码是分类数据广泛使用的一种格式,也叫分类编码( categorical encoding)。
def to_one_hot(labels,dimension=46):
results=np.zeros((len(labels),dimension))
for i,label in enumerate(labels):
results[i,label]=1.
return results
one_hot_train_labels=to_one_hot(train_labels)
one_hot_test_data=to_one_hot(test_labels)
#使用内置函数
from keras.utils.np_utils import to_categorical
one_hot_train_labels=to_categorical(train_labels)
one_hot_test_labels=to_categorical(test_labels)
注:
- 这个主题分类问题与前面的电影评论分类问题类似,两个例子都是试图对简短的文本片段进行分类。但这个问题有一个新的约束条件:输出类别的数量从 2 个变为 46 个。输出空间的维度要大得多。
- 对于前面用过的 Dense 层的堆叠,每层只能访问上一层输出的信息。如果某一层丢失了与分类问题相关的一些信息,那么这些信息无法被后面的层找回,也就是说,每一层都可能成为信息瓶颈。上一个例子使用了 16 维的中间层,但对这个例子来说 16 维空间可能太小了,无法学会区分 46 个不同的类别。这种维度较小的层可能成为信息瓶颈,永久地丢失相关信息。
- 出于这个原因,下面将使用维度更大的层,包含 64 个单元。
#构建网络
from keras import models
from keras import layers
model=models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(64,activation='relu'))
model.add(layers.Dense(46,activation='softmax'))
注:model.add(layers.Dense(46,activation='softmax'))报错:TypeError: softmax() got an unexpected keyword argument 'axis'?
- 原来的配置:tensorflow1.4.0 keras2.1.6.
- 参照关于TypeError: softmax() got an unexpected keyword argument axis的解决方案_人工智能_dqefd2e4f1的博客-CSDN博客修改配置:
- tensorflow=1.5.0 keras=2.0.8 最后重启核.
- softmax函数(剖析Keras源码之激活函数softmax_人工智能_yuanyuneixin1的专栏-CSDN博客 ](https://blog.csdn.net/yuanyuneixin1/article/details/103753264)
将不会报错!
注:
- 网络的最后一层是大小为 46 的 Dense 层。这意味着,对于每个输入样本,网络都会输出一个 46 维向量。这个向量的每个元素(即每个维度)代表不同的输出类别。
- 最后一层使用了 softmax 激活。你在 MNIST 例子中见过这种用法。网络将输出在 46个不同输出类别上的概率分布——对于每一个输入样本,网络都会输出一个 46 维向量,其中 output[i] 是样本属于第 i 个类别的概率。 46 个概率的总和为 1。
- 对于这个例子,最好的损失函数是 categorical_crossentropy(分类交叉熵)。它用于衡量两个概率分布之间的距离,这里两个概率分布分别是网络输出的概率分布和标签的真实分布。通过将这两个分布的距离最小化,训练网络可使输出结果尽可能接近真实标签。
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
#留出验证集
from sklearn.model_selection import train_test_split
x_val,partial_x_train,y_val,partial_y_train=train_test_split(x_train,one_hot_train_labels,test_size=1000,random_state=12345)
print(x_val.shape,partial_x_train.shape,y_val.shape,partial_y_train.shape)
(7982, 10000) (1000, 10000) (7982, 46) (1000, 46)
#模型训练
history=model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val,y_val))
Train on 1000 samples, validate on 7982 samples
Epoch 1/20
1000/1000 [==============================] - 2s - loss: 3.7190 - acc: 0.2570 - val_loss: 3.3810 - val_acc: 0.4119
Epoch 2/20
1000/1000 [==============================] - 1s - loss: 3.1404 - acc: 0.5020 - val_loss: 2.8883 - val_acc: 0.4787
Epoch 3/20
1000/1000 [==============================] - 2s - loss: 2.5471 - acc: 0.5540 - val_loss: 2.5269 - val_acc: 0.5170
Epoch 4/20
1000/1000 [==============================] - 2s - loss: 2.0929 - acc: 0.5890 - val_loss: 2.2767 - val_acc: 0.5345
Epoch 5/20
1000/1000 [==============================] - 2s - loss: 1.7469 - acc: 0.6510 - val_loss: 2.0901 - val_acc: 0.5542
Epoch 6/20
1000/1000 [==============================] - 1s - loss: 1.4851 - acc: 0.6960 - val_loss: 1.9564 - val_acc: 0.5644
Epoch 7/20
1000/1000 [==============================] - 1s - loss: 1.2927 - acc: 0.7230 - val_loss: 1.8765 - val_acc: 0.5645
Epoch 8/20
1000/1000 [==============================] - 1s - loss: 1.1319 - acc: 0.7650 - val_loss: 1.7886 - val_acc: 0.5876
Epoch 9/20
1000/1000 [==============================] - 2s - loss: 0.9924 - acc: 0.8000 - val_loss: 1.7118 - val_acc: 0.6208
Epoch 10/20
1000/1000 [==============================] - 1s - loss: 0.8799 - acc: 0.8300 - val_loss: 1.6660 - val_acc: 0.6353
Epoch 11/20
1000/1000 [==============================] - 2s - loss: 0.7850 - acc: 0.8490 - val_loss: 1.6195 - val_acc: 0.6427
Epoch 12/20
1000/1000 [==============================] - 1s - loss: 0.7013 - acc: 0.8720 - val_loss: 1.5924 - val_acc: 0.6480
Epoch 13/20
1000/1000 [==============================] - 1s - loss: 0.6261 - acc: 0.8920 - val_loss: 1.5671 - val_acc: 0.6507
Epoch 14/20
1000/1000 [==============================] - 2s - loss: 0.5618 - acc: 0.9040 - val_loss: 1.5389 - val_acc: 0.6571
Epoch 15/20
1000/1000 [==============================] - 2s - loss: 0.5050 - acc: 0.9170 - val_loss: 1.5127 - val_acc: 0.6669
Epoch 16/20
1000/1000 [==============================] - 1s - loss: 0.4539 - acc: 0.9290 - val_loss: 1.5007 - val_acc: 0.6681
Epoch 17/20
1000/1000 [==============================] - 1s - loss: 0.4064 - acc: 0.9460 - val_loss: 1.4882 - val_acc: 0.6704
Epoch 18/20
1000/1000 [==============================] - 1s - loss: 0.3644 - acc: 0.9520 - val_loss: 1.4782 - val_acc: 0.6731
Epoch 19/20
1000/1000 [==============================] - 1s - loss: 0.3261 - acc: 0.9580 - val_loss: 1.4771 - val_acc: 0.6744
Epoch 20/20
1000/1000 [==============================] - 2s - loss: 0.2914 - acc: 0.9640 - val_loss: 1.4711 - val_acc: 0.6761
history_dict=history.history
print(history_dict.keys())
dict_keys(['val_loss', 'val_acc', 'loss', 'acc'])
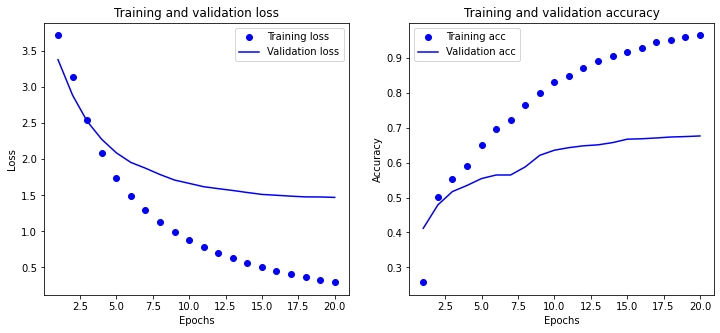
#绘制训练损失和验证损失
import matplotlib.pyplot as plt
loss_values=history_dict['loss']
val_loss_values=history_dict['val_loss']
epochs=range(1,len(loss_values)+1)
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(12,5))
Axes=axes.flatten()
#绘制训练损失和验证损失
Axes[0].plot(epochs,loss_values,'bo',label='Training loss')
Axes[0].plot(epochs,val_loss_values,'b',label='Validation loss')
Axes[0].set_title('Training and validation loss')
Axes[0].set_xlabel('Epochs')
Axes[0].set_ylabel('Loss')
Axes[0].legend()
#训练训练精度和验证精度
acc=history_dict['acc']
val_acc=history_dict['val_acc']
Axes[1].plot(epochs,acc,'bo',label='Training acc')
Axes[1].plot(epochs,val_acc,'b',label='Validation acc')
Axes[1].set_title('Training and validation accuracy')
Axes[1].set_xlabel('Epochs')
Axes[1].set_ylabel('Accuracy')
Axes[1].legend()
plt.show()
#重新训练一个新的网络
model=models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(64,activation='relu'))
model.add(layers.Dense(46,activation='softmax'))
model.compile(
optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=9,
batch_size=512,
validation_data=(x_val,y_val))
results=model.evaluate(x_test,one_hot_test_labels)
Train on 1000 samples, validate on 7982 samples
Epoch 1/9
1000/1000 [==============================] - 2s - loss: 3.7028 - acc: 0.2430 - val_loss: 3.3254 - val_acc: 0.4801
Epoch 2/9
1000/1000 [==============================] - 1s - loss: 3.0536 - acc: 0.5380 - val_loss: 2.7722 - val_acc: 0.5229
Epoch 3/9
1000/1000 [==============================] - 1s - loss: 2.3973 - acc: 0.5660 - val_loss: 2.3857 - val_acc: 0.5474
Epoch 4/9
1000/1000 [==============================] - 1s - loss: 1.9276 - acc: 0.6510 - val_loss: 2.1499 - val_acc: 0.5484
Epoch 5/9
1000/1000 [==============================] - 1s - loss: 1.6058 - acc: 0.6970 - val_loss: 1.9552 - val_acc: 0.5906
Epoch 6/9
1000/1000 [==============================] - 1s - loss: 1.3476 - acc: 0.7520 - val_loss: 1.8334 - val_acc: 0.6118
Epoch 7/9
1000/1000 [==============================] - 1s - loss: 1.1597 - acc: 0.7830 - val_loss: 1.7383 - val_acc: 0.6318
Epoch 8/9
1000/1000 [==============================] - 1s - loss: 1.0092 - acc: 0.8160 - val_loss: 1.6727 - val_acc: 0.6407
Epoch 9/9
1000/1000 [==============================] - 2s - loss: 0.8877 - acc: 0.8390 - val_loss: 1.6122 - val_acc: 0.6585
2208/2246 [============================>.] - ETA: 0s
print(results)
[1.6328595385207518, 0.6607301870521858]
import copy
test_labels_copy=copy.copy(test_labels)
np.random.shuffle(test_labels_copy)
hits_array = np.array(test_labels) == np.array(test_labels_copy)
float(np.sum(hits_array)) / len(test_labels)
0.17764915405164738
注:
这种方法可以得到约 80%(个人只有66%) 的精度。对于平衡的二分类问题,完全随机的分类器能够得到50% 的精度。但在这个例子中,完全随机的精度约为 19%(个人18%),所以上述结果相当不错,至少和随机的基准比起来还不错。
predictions=model.predict(x_test)
print(predictions.shape)
(2246, 46)
#最大的元素就是预测类别,即概率最大的类别
y_pred=np.argmax(predictions,axis=1)
y_true=np.argmax(one_hot_test_labels,axis=1)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_true,y_pred)
array([[ 0, 3, 0, ..., 0, 0, 0],
[ 0, 74, 0, ..., 0, 0, 0],
[ 0, 9, 0, ..., 0, 0, 0],
...,
[ 0, 2, 0, ..., 2, 0, 0],
[ 0, 1, 0, ..., 0, 0, 0],
[ 0, 0, 0, ..., 0, 0, 0]], dtype=int64)
#验证中间维度的重要性:准确率58%
#重新训练一个新的网络
model=models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(4,activation='relu'))
model.add(layers.Dense(46,activation='softmax'))
model.compile(
optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=128,
validation_data=(x_val,y_val))
results=model.evaluate(x_test,one_hot_test_labels)
print(results)
Train on 1000 samples, validate on 7982 samples
Epoch 1/20
1000/1000 [==============================] - 2s - loss: 3.7911 - acc: 0.0310 - val_loss: 3.7182 - val_acc: 0.0392
Epoch 2/20
1000/1000 [==============================] - 2s - loss: 3.6316 - acc: 0.0500 - val_loss: 3.6050 - val_acc: 0.0353
Epoch 3/20
1000/1000 [==============================] - 2s - loss: 3.4741 - acc: 0.0730 - val_loss: 3.4998 - val_acc: 0.0492
Epoch 4/20
1000/1000 [==============================] - 2s - loss: 3.3161 - acc: 0.0850 - val_loss: 3.3881 - val_acc: 0.0510
Epoch 5/20
1000/1000 [==============================] - 2s - loss: 3.1592 - acc: 0.0970 - val_loss: 3.2817 - val_acc: 0.0573
Epoch 6/20
1000/1000 [==============================] - 2s - loss: 2.9879 - acc: 0.1220 - val_loss: 3.1765 - val_acc: 0.1793
Epoch 7/20
1000/1000 [==============================] - 2s - loss: 2.8128 - acc: 0.2730 - val_loss: 3.0404 - val_acc: 0.2483
Epoch 8/20
1000/1000 [==============================] - 2s - loss: 2.6299 - acc: 0.2970 - val_loss: 2.9262 - val_acc: 0.2541
Epoch 9/20
1000/1000 [==============================] - 1s - loss: 2.4480 - acc: 0.3000 - val_loss: 2.8121 - val_acc: 0.2675
Epoch 10/20
1000/1000 [==============================] - 2s - loss: 2.2736 - acc: 0.3020 - val_loss: 2.6856 - val_acc: 0.2640
Epoch 11/20
1000/1000 [==============================] - 2s - loss: 2.1041 - acc: 0.3040 - val_loss: 2.5970 - val_acc: 0.2684
Epoch 12/20
1000/1000 [==============================] - 2s - loss: 1.9482 - acc: 0.3040 - val_loss: 2.4678 - val_acc: 0.2642
Epoch 13/20
1000/1000 [==============================] - 2s - loss: 1.7972 - acc: 0.3040 - val_loss: 2.4264 - val_acc: 0.2689
Epoch 14/20
1000/1000 [==============================] - 2s - loss: 1.6472 - acc: 0.4030 - val_loss: 2.3173 - val_acc: 0.5169
Epoch 15/20
1000/1000 [==============================] - 2s - loss: 1.5000 - acc: 0.6720 - val_loss: 2.2494 - val_acc: 0.5416
Epoch 16/20
1000/1000 [==============================] - 2s - loss: 1.3657 - acc: 0.6830 - val_loss: 2.1867 - val_acc: 0.5490
Epoch 17/20
1000/1000 [==============================] - 2s - loss: 1.2502 - acc: 0.6880 - val_loss: 2.0991 - val_acc: 0.5695
Epoch 18/20
1000/1000 [==============================] - 2s - loss: 1.1553 - acc: 0.6990 - val_loss: 2.0940 - val_acc: 0.5723
Epoch 19/20
1000/1000 [==============================] - 2s - loss: 1.0724 - acc: 0.7260 - val_loss: 2.0683 - val_acc: 0.5811
Epoch 20/20
1000/1000 [==============================] - 2s - loss: 1.0063 - acc: 0.7470 - val_loss: 2.0576 - val_acc: 0.5862
2176/2246 [============================>.] - ETA: 0s[2.1026238074604144, 0.5819234194122885]
#验证中间维度的重要性:32个隐藏单元,准确率71%
#重新训练一个新的网络
model=models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(32,activation='relu'))
model.add(layers.Dense(46,activation='softmax'))
model.compile(
optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=128,
validation_data=(x_val,y_val))
results=model.evaluate(x_test,one_hot_test_labels)
print(results)
Train on 1000 samples, validate on 7982 samples
Epoch 1/20
1000/1000 [==============================] - 2s - loss: 3.4260 - acc: 0.3100 - val_loss: 2.8872 - val_acc: 0.5085
Epoch 2/20
1000/1000 [==============================] - 2s - loss: 2.3377 - acc: 0.5830 - val_loss: 2.2268 - val_acc: 0.5501
Epoch 3/20
1000/1000 [==============================] - 2s - loss: 1.6347 - acc: 0.6930 - val_loss: 1.8780 - val_acc: 0.6317
Epoch 4/20
1000/1000 [==============================] - 2s - loss: 1.2201 - acc: 0.7790 - val_loss: 1.6869 - val_acc: 0.65750
Epoch 5/20
1000/1000 [==============================] - 2s - loss: 0.9387 - acc: 0.8220 - val_loss: 1.5694 - val_acc: 0.6792
Epoch 6/20
1000/1000 [==============================] - 2s - loss: 0.7306 - acc: 0.8670 - val_loss: 1.5090 - val_acc: 0.6718
Epoch 7/20
1000/1000 [==============================] - 2s - loss: 0.5763 - acc: 0.8940 - val_loss: 1.4532 - val_acc: 0.6802
Epoch 8/20
1000/1000 [==============================] - 2s - loss: 0.4569 - acc: 0.9260 - val_loss: 1.4229 - val_acc: 0.6873
Epoch 9/20
1000/1000 [==============================] - 2s - loss: 0.3643 - acc: 0.9460 - val_loss: 1.3973 - val_acc: 0.6977
Epoch 10/20
1000/1000 [==============================] - 2s - loss: 0.2897 - acc: 0.9570 - val_loss: 1.3989 - val_acc: 0.6957
Epoch 11/20
1000/1000 [==============================] - 2s - loss: 0.2319 - acc: 0.9670 - val_loss: 1.4184 - val_acc: 0.6941
Epoch 12/20
1000/1000 [==============================] - 2s - loss: 0.1817 - acc: 0.9760 - val_loss: 1.4184 - val_acc: 0.6993
Epoch 13/20
1000/1000 [==============================] - 1s - loss: 0.1427 - acc: 0.9830 - val_loss: 1.4141 - val_acc: 0.7060
Epoch 14/20
1000/1000 [==============================] - 2s - loss: 0.1132 - acc: 0.9870 - val_loss: 1.4141 - val_acc: 0.7075
Epoch 15/20
1000/1000 [==============================] - 2s - loss: 0.0877 - acc: 0.9900 - val_loss: 1.4143 - val_acc: 0.7156
Epoch 16/20
1000/1000 [==============================] - 2s - loss: 0.0673 - acc: 0.9910 - val_loss: 1.4332 - val_acc: 0.71270.9
Epoch 17/20
1000/1000 [==============================] - 2s - loss: 0.0551 - acc: 0.9910 - val_loss: 1.4719 - val_acc: 0.7126
Epoch 18/20
1000/1000 [==============================] - 2s - loss: 0.0434 - acc: 0.9930 - val_loss: 1.4835 - val_acc: 0.7130
Epoch 19/20
1000/1000 [==============================] - 2s - loss: 0.0354 - acc: 0.9960 - val_loss: 1.5006 - val_acc: 0.7161
Epoch 20/20
1000/1000 [==============================] - 2s - loss: 0.0295 - acc: 0.9930 - val_loss: 1.5302 - val_acc: 0.7156
2176/2246 [============================>.] - ETA: 0s[1.581864387141947, 0.7052537845588643]
#验证中间维度的重要性:128个隐藏单元,准确率71%,未增加
#重新训练一个新的网络
model=models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(128,activation='relu'))
model.add(layers.Dense(46,activation='softmax'))
model.compile(
optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=128,
validation_data=(x_val,y_val))
results=model.evaluate(x_test,one_hot_test_labels)
print(results)
Train on 1000 samples, validate on 7982 samples
Epoch 1/20
1000/1000 [==============================] - 2s - loss: 3.0798 - acc: 0.4140 - val_loss: 2.2990 - val_acc: 0.4930
Epoch 2/20
1000/1000 [==============================] - 2s - loss: 1.7348 - acc: 0.6320 - val_loss: 1.7799 - val_acc: 0.5948
Epoch 3/20
1000/1000 [==============================] - 2s - loss: 1.2176 - acc: 0.7360 - val_loss: 1.5994 - val_acc: 0.6490
Epoch 4/20
1000/1000 [==============================] - 2s - loss: 0.9145 - acc: 0.8090 - val_loss: 1.4957 - val_acc: 0.6783
Epoch 5/20
1000/1000 [==============================] - 2s - loss: 0.6999 - acc: 0.8580 - val_loss: 1.4199 - val_acc: 0.6887
Epoch 6/20
1000/1000 [==============================] - 2s - loss: 0.5349 - acc: 0.9080 - val_loss: 1.3807 - val_acc: 0.6999
Epoch 7/20
1000/1000 [==============================] - 2s - loss: 0.4050 - acc: 0.9320 - val_loss: 1.3455 - val_acc: 0.7050
Epoch 8/20
1000/1000 [==============================] - 2s - loss: 0.3031 - acc: 0.9630 - val_loss: 1.3325 - val_acc: 0.7124
Epoch 9/20
1000/1000 [==============================] - 2s - loss: 0.2237 - acc: 0.9750 - val_loss: 1.3138 - val_acc: 0.7226
Epoch 10/20
1000/1000 [==============================] - 2s - loss: 0.1591 - acc: 0.9820 - val_loss: 1.3621 - val_acc: 0.7115
Epoch 11/20
1000/1000 [==============================] - 2s - loss: 0.1145 - acc: 0.9840 - val_loss: 1.3353 - val_acc: 0.7273
Epoch 12/20
1000/1000 [==============================] - 2s - loss: 0.0801 - acc: 0.9910 - val_loss: 1.3492 - val_acc: 0.7221
Epoch 13/20
1000/1000 [==============================] - 2s - loss: 0.0603 - acc: 0.9930 - val_loss: 1.3493 - val_acc: 0.7334
Epoch 14/20
1000/1000 [==============================] - 2s - loss: 0.0460 - acc: 0.9940 - val_loss: 1.3759 - val_acc: 0.7259
Epoch 15/20
1000/1000 [==============================] - 2s - loss: 0.0335 - acc: 0.9950 - val_loss: 1.3890 - val_acc: 0.7331
Epoch 16/20
1000/1000 [==============================] - 2s - loss: 0.0267 - acc: 0.9950 - val_loss: 1.4839 - val_acc: 0.7211
Epoch 17/20
1000/1000 [==============================] - 2s - loss: 0.0217 - acc: 0.9940 - val_loss: 1.4429 - val_acc: 0.7296
Epoch 18/20
1000/1000 [==============================] - 2s - loss: 0.0169 - acc: 0.9950 - val_loss: 1.4571 - val_acc: 0.7365
Epoch 19/20
1000/1000 [==============================] - 2s - loss: 0.0154 - acc: 0.9950 - val_loss: 1.4853 - val_acc: 0.7280
Epoch 20/20
1000/1000 [==============================] - 2s - loss: 0.0112 - acc: 0.9960 - val_loss: 1.5115 - val_acc: 0.7313
2112/2246 [===========================>..] - ETA: 0s[1.5476579676752948, 0.7159394479604672]
#验证中间维度的重要性:一个隐藏层,准确率72%
#重新训练一个新的网络
model=models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
#model.add(layers.Dense(32,activation='relu'))
model.add(layers.Dense(46,activation='softmax'))
model.compile(
optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=128,
validation_data=(x_val,y_val))
results=model.evaluate(x_test,one_hot_test_labels)
print(results)
Train on 1000 samples, validate on 7982 samples
Epoch 1/20
1000/1000 [==============================] - 2s - loss: 3.3507 - acc: 0.4410 - val_loss: 2.7851 - val_acc: 0.5682
Epoch 2/20
1000/1000 [==============================] - 1s - loss: 2.2370 - acc: 0.6660 - val_loss: 2.1916 - val_acc: 0.6245
Epoch 3/20
1000/1000 [==============================] - 2s - loss: 1.5662 - acc: 0.7600 - val_loss: 1.8646 - val_acc: 0.6506
Epoch 4/20
1000/1000 [==============================] - 2s - loss: 1.1541 - acc: 0.8100 - val_loss: 1.6695 - val_acc: 0.6706
Epoch 5/20
1000/1000 [==============================] - 2s - loss: 0.8744 - acc: 0.8590 - val_loss: 1.5402 - val_acc: 0.6867
Epoch 6/20
1000/1000 [==============================] - 2s - loss: 0.6714 - acc: 0.8980 - val_loss: 1.4544 - val_acc: 0.6971
Epoch 7/20
1000/1000 [==============================] - 2s - loss: 0.5207 - acc: 0.9270 - val_loss: 1.3934 - val_acc: 0.7037
Epoch 8/20
1000/1000 [==============================] - 2s - loss: 0.4029 - acc: 0.9510 - val_loss: 1.3484 - val_acc: 0.7110
Epoch 9/20
1000/1000 [==============================] - 2s - loss: 0.3116 - acc: 0.9620 - val_loss: 1.3183 - val_acc: 0.7141
Epoch 10/20
1000/1000 [==============================] - 2s - loss: 0.2415 - acc: 0.9720 - val_loss: 1.3024 - val_acc: 0.7176
Epoch 11/20
1000/1000 [==============================] - 2s - loss: 0.1882 - acc: 0.9820 - val_loss: 1.2922 - val_acc: 0.7202
Epoch 12/20
1000/1000 [==============================] - 2s - loss: 0.1451 - acc: 0.9850 - val_loss: 1.2912 - val_acc: 0.7216
Epoch 13/20
1000/1000 [==============================] - 2s - loss: 0.1145 - acc: 0.9900 - val_loss: 1.2879 - val_acc: 0.72410.9
Epoch 14/20
1000/1000 [==============================] - 2s - loss: 0.0894 - acc: 0.9910 - val_loss: 1.2864 - val_acc: 0.7276
Epoch 15/20
1000/1000 [==============================] - 2s - loss: 0.0712 - acc: 0.9920 - val_loss: 1.2991 - val_acc: 0.7274
Epoch 16/20
1000/1000 [==============================] - 2s - loss: 0.0564 - acc: 0.9920 - val_loss: 1.3104 - val_acc: 0.7279
Epoch 17/20
1000/1000 [==============================] - 2s - loss: 0.0457 - acc: 0.9910 - val_loss: 1.3191 - val_acc: 0.7301
Epoch 18/20
1000/1000 [==============================] - 2s - loss: 0.0385 - acc: 0.9910 - val_loss: 1.3317 - val_acc: 0.7296
Epoch 19/20
1000/1000 [==============================] - 2s - loss: 0.0290 - acc: 0.9940 - val_loss: 1.3557 - val_acc: 0.7283
Epoch 20/20
1000/1000 [==============================] - 2s - loss: 0.0275 - acc: 0.9940 - val_loss: 1.3766 - val_acc: 0.7288
2240/2246 [============================>.] - ETA: 0s[1.4121944055107165, 0.716384683935534]
#验证中间维度的重要性:3个隐藏层,准确率64%
#重新训练一个新的网络
model=models.Sequential()
model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
model.add(layers.Dense(128,activation='relu'))
model.add(layers.Dense(32,activation='relu'))
model.add(layers.Dense(46,activation='softmax'))
model.compile(
optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=128,
validation_data=(x_val,y_val))
results=model.evaluate(x_test,one_hot_test_labels)
print(results)
Train on 1000 samples, validate on 7982 samples
Epoch 1/20
1000/1000 [==============================] - 2s - loss: 3.2393 - acc: 0.3370 - val_loss: 2.4314 - val_acc: 0.4326
Epoch 2/20
1000/1000 [==============================] - 2s - loss: 1.9808 - acc: 0.5450 - val_loss: 1.9284 - val_acc: 0.5823
Epoch 3/20
1000/1000 [==============================] - 2s - loss: 1.4943 - acc: 0.6850 - val_loss: 1.7668 - val_acc: 0.6082
Epoch 4/20
1000/1000 [==============================] - 2s - loss: 1.1805 - acc: 0.7450 - val_loss: 1.6545 - val_acc: 0.6267
Epoch 5/20
1000/1000 [==============================] - 2s - loss: 0.9341 - acc: 0.7920 - val_loss: 1.5798 - val_acc: 0.6635
Epoch 6/20
1000/1000 [==============================] - 2s - loss: 0.7301 - acc: 0.8450 - val_loss: 1.5412 - val_acc: 0.67730.849
Epoch 7/20
1000/1000 [==============================] - 2s - loss: 0.5585 - acc: 0.8890 - val_loss: 1.4969 - val_acc: 0.6868
Epoch 8/20
1000/1000 [==============================] - 2s - loss: 0.4301 - acc: 0.9070 - val_loss: 1.5158 - val_acc: 0.6839
Epoch 9/20
1000/1000 [==============================] - 2s - loss: 0.3289 - acc: 0.9290 - val_loss: 1.5401 - val_acc: 0.6721
Epoch 10/20
1000/1000 [==============================] - 2s - loss: 0.2564 - acc: 0.9500 - val_loss: 1.5659 - val_acc: 0.6892
Epoch 11/20
1000/1000 [==============================] - 2s - loss: 0.1939 - acc: 0.9610 - val_loss: 1.5217 - val_acc: 0.7023
Epoch 12/20
1000/1000 [==============================] - 2s - loss: 0.1388 - acc: 0.9840 - val_loss: 1.5936 - val_acc: 0.6944
Epoch 13/20
1000/1000 [==============================] - 2s - loss: 0.1036 - acc: 0.9880 - val_loss: 1.5633 - val_acc: 0.7061
Epoch 14/20
1000/1000 [==============================] - 2s - loss: 0.0720 - acc: 0.9910 - val_loss: 1.7625 - val_acc: 0.6729
Epoch 15/20
1000/1000 [==============================] - 2s - loss: 0.0537 - acc: 0.9920 - val_loss: 1.6561 - val_acc: 0.6944
Epoch 16/20
1000/1000 [==============================] - 2s - loss: 0.0421 - acc: 0.9930 - val_loss: 1.7160 - val_acc: 0.6992
Epoch 17/20
1000/1000 [==============================] - 2s - loss: 0.0298 - acc: 0.9950 - val_loss: 1.8821 - val_acc: 0.6776
Epoch 18/20
1000/1000 [==============================] - 2s - loss: 0.0261 - acc: 0.9940 - val_loss: 1.7448 - val_acc: 0.6994
Epoch 19/20
1000/1000 [==============================] - 2s - loss: 0.0220 - acc: 0.9940 - val_loss: 1.8322 - val_acc: 0.7021
Epoch 20/20
1000/1000 [==============================] - 2s - loss: 0.0146 - acc: 0.9960 - val_loss: 2.0921 - val_acc: 0.6634
2208/2246 [============================>.] - ETA: 0s[2.1851936431198595, 0.6447016919232433]
小结:
- 如果要对 N 个类别的数据点进行分类,网络的最后一层应该是大小为 N 的 Dense 层。
- 对于单标签、多分类问题,网络的最后一层应该使用 softmax 激活,这样可以输出在 N个输出类别上的概率分布。
- 这种问题的损失函数几乎总是应该使用分类交叉熵。它将网络输出的概率分布与目标的真实分布之间的距离最小化。
- 处理多分类问题的标签有两种方法。
- 通过分类编码(也叫 one-hot 编码)对标签进行编码,然后使用 categorical_crossentropy 作为损失函数。
- 将标签编码为整数,然后使用 sparse_categorical_crossentropy 损失函数。
- 如果你需要将数据划分到许多类别中,应该避免使用太小的中间层,以免在网络中造成信息瓶颈。
案例3:预测房价:回归问题
数据集:波士顿房价数据集
任务:本节将要预测 20 世纪 70 年代中期波士顿郊区房屋价格的中位数,已知当时郊区的一些数据点,比如犯罪率、当地房产税率等。本节用到的数据集与前面两个例子有一个有趣的区别。它包含的数据点相对较少,只有 506 个,分为 404 个训练样本和 102 个测试样本。输入数据的每个特征(比如犯罪率)都有不同的取值范围。例如,有些特性是比例,取值范围为 0~1;有的取值范围为 1~12;还有的取值范围为 0~100,等等。
#加载数据
from keras.datasets import boston_housing
(train_data,train_targets),(test_data,test_targets)=boston_housing.load_data()
print(train_data.shape,test_data.shape)
(404, 13) (102, 13)
test_targets
#单位*1000
array([ 7.2, 18.8, 19. , 27. , 22.2, 24.5, 31.2, 22.9, 20.5, 23.2, 18.6,
14.5, 17.8, 50. , 20.8, 24.3, 24.2, 19.8, 19.1, 22.7, 12. , 10.2,
20. , 18.5, 20.9, 23. , 27.5, 30.1, 9.5, 22. , 21.2, 14.1, 33.1,
23.4, 20.1, 7.4, 15.4, 23.8, 20.1, 24.5, 33. , 28.4, 14.1, 46.7,
32.5, 29.6, 28.4, 19.8, 20.2, 25. , 35.4, 20.3, 9.7, 14.5, 34.9,
26.6, 7.2, 50. , 32.4, 21.6, 29.8, 13.1, 27.5, 21.2, 23.1, 21.9,
13. , 23.2, 8.1, 5.6, 21.7, 29.6, 19.6, 7. , 26.4, 18.9, 20.9,
28.1, 35.4, 10.2, 24.3, 43.1, 17.6, 15.4, 16.2, 27.1, 21.4, 21.5,
22.4, 25. , 16.6, 18.6, 22. , 42.8, 35.1, 21.5, 36. , 21.9, 24.1,
50. , 26.7, 25. ])
np.mean(test_targets)
23.07843137254902
#数据标准化
from sklearn.preprocessing import StandardScaler
data_scaler=StandardScaler().fit(train_data)
train_data=data_scaler.transform(train_data)
test_data=data_scaler.transform(test_data)
target_scaler=StandardScaler().fit(train_targets.reshape((-1,1)))
train_targets=target_scaler.transform(train_targets.reshape((-1,1)))
train_targets=train_targets.flatten()
test_targets=target_scaler.transform(test_targets.reshape((-1,1)))
test_targets=test_targets.flatten()
#定义模型
from keras import models
from keras import layers
def build_model():
model=models.Sequential()
model.add(layers.Dense(64,activation='relu',
input_shape=(train_data.shape[1],)))
model.add(layers.Dense(64,activation='relu'))
model.add(layers.Dense(1))
model.compile(optimizer='rmsprop',loss='mse',metrics=['mae'])
return model
注:
- 网络的最后一层只有一个单元,没有激活,是一个线性层。这是标量回归(标量回归是预测单一连续值的回归)的典型设置。添加激活函数将会限制输出范围。例如,如果向最后一层添加 sigmoid 激活函数,网络只能学会预测 0~1 范围内的值。这里最后一层是纯线性的,所以网络可以学会预测任意范围内的值。
- 注意,编译网络用的是 mse 损失函数,即均方误差( MSE, mean squared error),预测值与目标值之差的平方。这是回归问题常用的损失函数。
- 在训练过程中还监控一个新指标: 平均绝对误差( MAE, mean absolute error)。它是预测值与目标值之差的绝对值。比如,如果这个问题的 MAE 等于 0.5,就表示你预测的房价与实际价格平均相差 500 美元。
#使用K折交叉验证
import numpy as np
k=4
num_val_samples=len(train_data)//4
num_epochs=500
all_mae_histories=[]
for i in range(k):
print('propressing fold #',i)
val_data=train_data[i*num_val_samples:(i+1)*num_val_samples]
val_targets=train_targets[i*num_val_samples:(i+1)*num_val_samples]
partial_train_data=np.concatenate(
[train_data[:i*num_val_samples],train_data[(i+1)*num_val_samples:]],
axis=0)
#print(partial_train_data.shape)
partial_train_targets=np.concatenate(
[train_targets[:i*num_val_samples],train_targets[(i+1)*num_val_samples:]],
axis=0)
#构建已编译的Keras模型
model=build_model()
#训练模式(静默模式)
history=model.fit(partial_train_data,partial_train_targets,epochs=num_epochs,
batch_size=1,verbose=0,validation_data=(val_data,val_targets))
#val_mse,val_mae=model.evaluate(val_data,val_targets,verbose=0)
history_dict=history.history
print(history_dict.keys())
mae_history=history.history['val_mean_absolute_error']
all_mae_histories.append(mae_history)
propressing fold # 0
dict_keys(['val_loss', 'val_mean_absolute_error', 'loss', 'mean_absolute_error'])
propressing fold # 1
dict_keys(['val_loss', 'val_mean_absolute_error', 'loss', 'mean_absolute_error'])
propressing fold # 2
dict_keys(['val_loss', 'val_mean_absolute_error', 'loss', 'mean_absolute_error'])
propressing fold # 3
dict_keys(['val_loss', 'val_mean_absolute_error', 'loss', 'mean_absolute_error'])
#计算所有轮次中的K折验证分数平均值
average_mae_history=[
np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]
#绘制验证分数
import matplotlib.pyplot as plt
fig=plt.figure(figsize=(12,5))
plt.plot(range(1,len(average_mae_history)+1),average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('validation MAE')
plt.show()
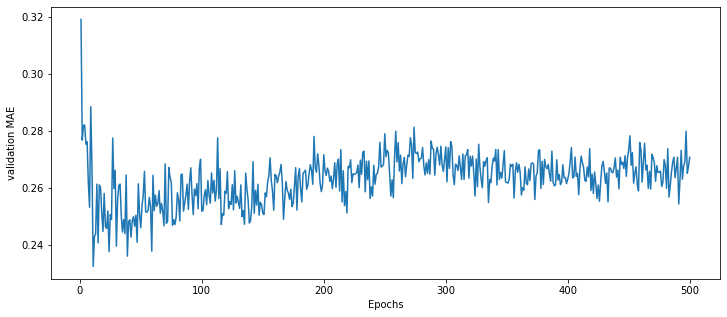
mae还是偏大,可以通过增加
num_epochs进行更准确的优化。
#训练的最终模型
model=build_model()
history=model.fit(train_data,train_targets,
epochs=80,batch_size=16,verbose=0)
test_mse_score,test_mae_score=model.evaluate(test_data,test_targets)
32/102 [========>.....................] - ETA: 1s
test_mse_score
0.17438595084583058
test_mae_score
0.26517656153323604
target_scaler.inverse_transform([test_mae_score])
#预测值与真实值相差24.83*1000元,差异还是比较大(ps:郁闷,和书上的不一样。。。(书上预测相差2550元))
array([24.83441809])
小结:
- 回归问题使用的损失函数与分类问题不同。回归常用的损失函数是均方误差( MSE)。
- 同样,回归问题使用的评估指标也与分类问题不同。显而易见,精度的概念不适用于回归问题。常见的回归指标是平均绝对误差( MAE)。
- 如果输入数据的特征具有不同的取值范围,应该先进行预处理,对每个特征单独进行缩放。
- 如果可用的数据很少,使用 K 折验证可以可靠地评估模型。
- 如果可用的训练数据很少,最好使用隐藏层较少(通常只有一到两个)的小型网络,以避免严重的过拟合。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号