「CEOI2021」 Newspapers 题解 翻译
「CEOI2021」 Newspapers 官方题解 翻译
\(~~~~\) 看了一晚上终于勉强理解了。本质是精妙的构造。
\(~~~~\) 我不生产题解,我只是题解的搬运工。
\(~~~~\) 下面的翻译可能部分地方不太准确,还有部分可能会加入个人理解及勘误。也欢迎指正我的错误。
一、Branko 在存在环时不会被抓住
\(~~~~\) 对该问题进行最简单的观察可以得到:若 Ankica 存在成功的策略,输入的图至少应该是一棵树。
\(~~~~\) 为了证明这个结论,我们可以类推第二个样例。具体地,我们假定给出的图有一个环,我们可以假想 Branko 初始时在任意一个非 \(a_1\) 的环上结点。由于每一个环上的结点都有两个相邻的环上结点,则第 \(i\) 轮时 Branko 只需移动到与 \(a_i\) 相异的结点上。
二、一种暴力方法
\(~~~~\) 注意到 Ankica 只需掌握在每一回合前 Branko 可能存在的结点集合。当然,在游戏开始前,这个集合应该为这张图的点集。
\(~~~~\) 这引导我们将游戏表示为一张所有结点都是 Branko 可能存在的点的有向图,而有向边 \((u,v)\) 则表示:若上一个回合 Branko 可能在 \(u\) 结点,则下回合 Ankica 可能猜测的结点应包含 \(v\) 结点。
\(~~~~\) 显然,我们想找的是最短的使得这个集合从点集变为空集的路径。
\(~~~~\) 这种方法的时间足以通过 Subtask1。
\(~~~~\) (以下部分是译者的举例)
\(~~~~\) 以样例 \(1\) 为例,初始时 Branko 可能存在的结点是 \(\{1,2,3,4,5,6,7\}\) ,当我们猜测 \(1\) 后,相当于这一轮的集合应除去 \(1\) ,然后变为其余点一步可能到达的集合,即 \(\{1\}\) 。再猜测 \(1\) ,集合变为空集,故该样例的最优策略为 \(A=(1,1)\) 。
三、Branko 在链上会被抓住
\(~~~~\) 现在我们将说明 Ankica 一定可以在链上抓住 Branko。
\(~~~~\) 假设结点以 Subtask 2 的方式排列(即端点为 \(1\) 和 \(n\) 的链),现在我们将偶数点染为白色,奇数点染成黑色。
\(~~~~\) 当 \(N\) 为 \(1\) 或 \(2\) 时,我们可以轻松解决这个问题。在下面的部分我们假定 \(N\geq 3\) 。
\(~~~~\) 则 Ankica 有一种长为 \(2N-4\) 的策略:\((2,3,\dots,N-2,N-1,N-1,N-2,\dots,3,2)\) 。不难看出若 Branko 初始时在白色结点则他会在前 \(N-2\) 次猜测被抓住,否则会在后 \(N-2\) 次猜测被抓住。
\(~~~~\) 设想 Branko 初始时在白色结点。这样的话,在前 \(N-2\) 轮 Ankica 会与 Branko 始终处于同色结点。很容易发现为了使 Branko 在第 \(i\) 回合不被抓住,必定有 \(b_i>a_i\)。这是由于 \(b_1>a_1\) (否则 Branko 第一轮就会被抓住)而为使 \(b_i\) 始终小于 \(a_i\) ,必定有 \(b_j=a_j+1(j<i)\) 存在(若始终保持 \(b_i=a_i+2\) ,则在第 \(N-2\) 轮时 Branko 无处可走——译者注),然而由于 \(a_j\) 和 \(b_j\) 的奇偶性始终应该是相同的,这是不可能存在的。而当 \(a_{N-2}=N-1\) 时,没有在这个点之后的与 \(N-1\) 同色的点,因此我们可以得出” Branko 在前 \(N-2\) 轮必定会被抓住“的结论。
\(~~~~\) 若 Branko 初始时在黑色结点上,前 \(N-2\) 轮他会存在于与 Ankica 猜测结点颜色相异的结点上。由于第 \(N-1\) 轮重复猜测同一个结点,之后 Branko 将存在于与 Ankica 猜测结点颜色相同的结点上,所以,最后 \(N-2\) 轮会变为类似于前 \(N-2\) 轮的情况,只是方向相反。
\(~~~~\) 稍后我们将证明这个结论必定是最优的。
\(~~~~\) 一种在提交中常见的策略是 \((1,2,\dots,N,N,\dots,1)\)。
四、Branko 在一个有三叉且每条树枝长为 \(3\) 的图(\(S'\))上不会被抓住
\(~~~~\) 在这里我们将说明 Ankica 在以下这种特定的十个结点的图上不能抓住 Branko。将中心结点记为 \(10\) ,三条树枝为 \((1,2,3),(4,5,6),(7,8,9)\) ,如下图所示:
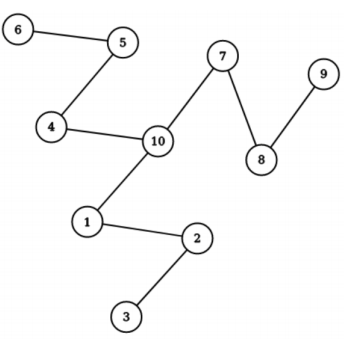
\(~~~~\) 我们可以说明 Branko 总可以通过偶数回合位于中心点 \(10\) 或在三条树枝的中间 \((2,4,8)\) (此处疑似笔误,应为 \((2,5,8)\) ——译者注)而不被抓住。大体来说,Branko会在整场游戏中尝试尽可能靠近中心结点。
\(~~~~\) 所以,如果 Branko 发现他在中心结点旁边,即 \(1,4,7\) 号结点中的一个,若下回合 Ankica 不猜测 \(10\) 号结点,他将移动到中心结点,否则他会移动到 \(2,4,8\) (此处疑似笔误,应为 \(2,5,8\) ——译者注)号结点中的一个。
\(~~~~\) 如果 Branko 发现他在树枝的中间,他会向 \(10\) 号结点移动,即到达 \(1,4,7\) 号结点中的一个,除非 Ankica 下回合猜测的是他要移动的结点。这样的话,他不得不移动到叶子 \(3,6,9\) 号结点中的一个。
\(~~~~\) 显然,如果 Branko 发现他在 \(3,6,9\) 号结点中的一个,依次地,他不得不移动到 \(2,4,8\) 号结点。
\(~~~~\) 核心想法在于,如果 Branko 发现他在中心结点,他将会移动到下一回合 Ankica 没有猜测的树枝或紧接着 Ankica 将连续猜测最靠近中心点的树枝,即 \((1,2),(4,5),(7,8)\) 。
\(~~~~\) 注意到我们只需要说明当下回合 Branko 旁边的结点被猜测时他绝对不会在叶子结点即可。为了使 Branko 到达叶子结点,Ankica 必须猜测在同一树枝上的靠近中间结点的结点。如果下回合 Ankica 能抓住 Branko ,这就意味着她猜测了两个与上一次结点相邻的结点,为了实现这个目的,她本应在最后一次访问 \(10\) 号结点后猜测其他树枝的一些连续结点。而这与她的猜测策略矛盾,Branko 可借此回到中心结点。
\(~~~~\) (这两段可能翻译有点问题,下面放上原文)
\(~~~~\) The key idea is that if Branko finds himself in the central node, he will move to a branch which Ankica will not guess in the next turn, or the next branch in which Ankica wlil guess two closest nodes to the central in succession, i.e. \((1, 2)\),$ (4, 5)$, or \((7, 8)\).
\(~~~~\) Notice that we only need to show that Branko will never be at a leaf node when Ankica guesses its neighbour on the next turn. In order for Branko to visit a leaf node, that means that Ankica must guess the node of the same arm next to the central one in that turn. If Ankica catches Branko on the next turn, that would imply her guessing two successive nodes from the previous section. For that to be possible, she would have to have guessed such consecutive nodes of some other arm after his last visit to node \(10\). This is in contradiction with the rules because during her guesses, he would have returned to the central node.
五、Branko 在不含 \(S'\) 的图上会被抓住
\(~~~~\) 总的来说,我们很好得出,若 Branko 在图 \(G\) 上会被抓住,则他也会在含有导出子图 \(G\) 的图 \(H\) 上被抓住。(疑似有误,个人理解是在图 \(G\) 上不会被抓住则在含有 \(G\) 的图 \(H\) 上也不会被抓住——译者注)换句话说,Branko 在不含 \(S'\) 的图上不会被抓住。
\(~~~~\) 有趣的是,事实证明 Ankica 在不含 \(S'\) 的图上总能抓住 Branko。我们可以通过使用与解决链上问题相似的方法来解决这一点。
\(~~~~\) 我们观察树上的最长路径(直径),假定其结点按顺序标号为 \(1,2,\dots,l\) ,其中 \(l\) 是直径的长度,我们同时也将在链上使用的染色方法进行扩展。当一个结点距离结点 \(1\) 为偶数时染成白色,否则染成黑色。注意到这样会将树分成两个部分。
\(~~~~\) 注意到 \(2\) 和 \(l-1\) 一定没有连接一条长度为 \(2\) 的非直径上的链,否则这与直径定义矛盾。
\(~~~~\) 最终,注意到其他结点一定没有连接长度为 \(3\) 的非直径上的链,否则这要么与直径定义矛盾,要么会导致图上出现 \(S'\).
\(~~~~\) 这意味着所有的非叶子结点要么在直径上要么与直径上的结点相邻。这使得我们可以为 Ankica 构造出与适用于链的策略相似的一种策略。在此,Ankica 将从 \(3\) 扫到 \(l-2\) 并返回,但同时把所有相邻的非叶子结点计算在内。
\(~~~~\) 具体来说,当她沿路线到达一个结点 \(i\) 时,她会遍历所有 \(i\) 的非叶子且非 \(i+1\) 的相邻结点,在猜测 \(i+1\) 前,她会在两次相邻的遍历间再次遍历结点 \(i\) 。遍历结点 \(l\) 后,她会按相同策略返回至结点 \(2\) 。
\(~~~~\) 通过与在第三部分提出的相似的推理,我们可以归纳得出:当 Branko 初始在白色结点时, Ankica 总能在前半程抓住 Branko,否则她总能在后半程抓住 Branko.
六、最优策略
\(~~~~\) 在前面部分所提到的最优策略中,我们可以把结点分为三类:叶子结点、内部结点(即 \(3,\dots,l-2\))、与内部结点相邻的非叶子结点。
\(~~~~\) Ankica 永远不会猜测叶子结点,会猜测两次与内部结点相邻的结点,猜测 \(2f(v)-2\) 次内部结点,其中 \(f(v)\) 是 \(v\) 相邻的非叶结点个数。我们将会说明 Branko 在任何一个结点 \(v\) 猜测次数减少时都不会被抓住。
\(~~~~\) 情况1 结点 \(v\) 与内部结点相邻
\(~~~~\) 由于 \(a_i=v\) 只对最多 \(1\) 个 \(i\) 成立,\(a_i\not= v\) 必定要么对所有偶数的 \(i\) 成立,要么对奇数的 \(i\) 成立。所以,总有一种方法使 Branko 任何时候在 \(v\) 和与 \(v\) 相邻的结点之间而不被抓住。
\(~~~~\) 情况2 结点 \(v\) 是内部结点
\(~~~~\) Branko 将会再次尝试尽可能靠近结点 \(v\) 。令 \(u_1,u_2,\dots,u_k\) 为 \(v\) 所有相邻的结点,\(u_i'\) 为 \(u_i\) 与 \(v\) 不同的相邻的点。
\(~~~~\) 在减少次数的情况下,Ankica 最多能猜测 \(2_k-3\) 次 \(u\) 结点,所以她最多在偶数轮猜测 \(k-2\) 次或奇数轮猜测 \(k-2\) 次。我们假定她在偶数轮猜测了 \(k-2\) 次,则我们让 Branko 在所有 \(a_i\not=v\) 的奇数轮停留在 \(v\) 结点。
\(~~~~\) 现在,我们可以将 Ankica 的猜测以在奇数轮猜测 \(v\) 为依据划分为最长序列。换句话说,我们关注一些 \(a_i,a_{i+2},\dots,a_{i+2l}\) 且全部等于 \(v\) ,但 \(a_{i-2},a_{i+2}\not= v\) 的序列(疑似笔误,应为 \(a_{i+2l+2}\not=v\)——译者注)。
\(~~~~\) 我们可以选择出与 \(a_{i-1},a_{i+1},a_{i+3},\dots,a_{i+2l+1}\) 相异的结点 \(u_j\),因为 \(l<k-2\) 。故在所有奇数轮,Branko 移动到 \(u_{j}'\) 。
\(~~~~\) 我们现在知道了所有奇数轮时 Branko 的位置。
\(~~~~\) 而对偶数轮来说,我们认为 Branko 在奇数轮所在位置的相邻结点。如果至少一回合他在 \(u_j'\),他会在相应的偶数轮位于 \(u_j\) 。如果在两个相邻的回合他都在 \(v\) 结点,他可以简单地选择那个 Ankica 在偶数轮不会猜测的 \(u_j\) 。
\(~~~~\) 这说明了前文所述的策略的确是最优的。
\(~~~~\) 声明: 这篇题解内所有解释都是说明性的而不是严谨的。严谨地证明每种情况需要繁杂地对每种特殊情况(如 \(l\leq 2\) 的树)和边界情况(如下标越界)等进行处理。我们相信这对掌握了主要思想的读者来说不难处理。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号