「氮氧碘磷%你赛」AVL 树
前言
\(~~~~\) 请不要问我为什么10.8的比赛我到今天才补题，也不要问我积压下来的20道题补得怎么样了。
题意
\(~~~~\) 给出一棵 \(n\) 个点的 AVL 树，求保留恰好 \(k\) 个点使得保留的树仍为 AVL 树且保留的点字典序最小的方案。
\(~~~~\) \(1\leq k\leq n\leq 5\times 10^5.\)
题解
\(~~~~\) 官方题解太简洁了，不适合我这种菜鸡。幸亏还有学长的博客 orz
\(~~~~\) 首先我们可以中序遍历二叉树，显然此时对于一棵BST来说遍历的顺序恰为 \(1 \sim n\)，为了使得保留下来的序列字典序最小，我们就会尽量想让当前点保留下来。由于保留某个点一定会保留它的祖先，先序遍历也是正确的。然后根据当前情况计算保留这个点需要再加入多少点，若仍然不超过 \(k\) 的限制则满足条件。（这一段基本就是官方题解，并且保留了精髓的“根据当前情况”
\(~~~~\) 那么怎么根据当前情况呢？首先我们可以求出一个高为 \(h\) 的 AVL 树至少有多少的点，具体来说设答案为 \(f_h\) ，则：
\(~~~~\) 这个dp比较简单，不过多赘述。
\(~~~~\) 然后就可以开始考虑怎么计算还需要额外加入多少节点，从某个欲加入的点开始向上跳，当你跳到某个点是 \(u\) 的左子树时，考虑 \(u\) 的右子树 \(v\) 应该保留的深度，其应该是当前跳到的点的子树深度 \(-1\) ……吗？并不一定，因为我们没有考虑当 \(u\) 也是右子树时 \(u\) 还有高度限制，比如下图：
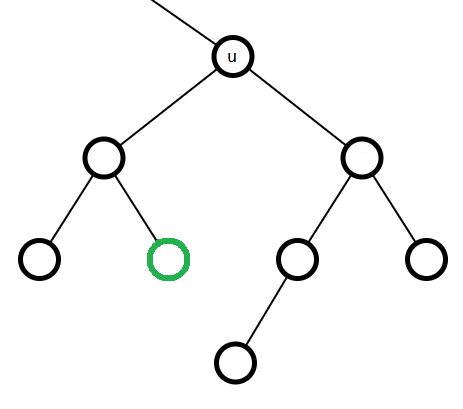
\(~~~~\) 假设当前子树的高度必须为 \(4\) （高度为 \(4\) 的 AVL 最少有7个点），最优的方案就一定是不选绿色点。但是假如我们不考虑整颗子树的高度限制，则在试图选择绿色点时我们会得到 \(u\) 的右子树高度只需为 \(1\) 满足条件从而使得整颗子树高度没有满足要求。
\(~~~~\) 因此我们维护一下每个点的子树高度最小值。每次加入一个点时其祖先的右子树都应打上相应的标记。同时这个标记还应该下传维护，则当左子树能容纳这个高度 \(h\) 时， \(h\) 下传至左子树，\(h-1\) 下传至右子树；否则 \(h\) 下传至右子树，\(h-1\) 下传至左子树。
代码
即使看懂了上面那些我的代码还是抄的
查看代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int n,k,dp[45],rt;//深度为i的AVL树至少有多少个节点（确定右子树的保留情况）
int ls[500005],rs[500005],fa[500005],MaxHeight[500005];
int dep[500005],MaxDep[500005],Ans[500005],h[500005];
void dfs(int u)
{
dep[u]=dep[fa[u]]+1;
MaxDep[u]=dep[u];
if(ls[u]) dfs(ls[u]),MaxDep[u]=max(MaxDep[u],MaxDep[ls[u]]);
if(rs[u]) dfs(rs[u]),MaxDep[u]=max(MaxDep[u],MaxDep[rs[u]]);
}
int Need(int x)
{
int y=max(dep[x],h[x]),ret=0;
while(x)
{
if(!Ans[x]) ret++;
y=max(y,h[x]);
if(ls[fa[x]]==x&&!Ans[rs[fa[x]]]) ret+=dp[max(y-1,MaxHeight[rs[fa[x]]])-dep[fa[x]]];
x=fa[x];
}
return ret;
}
void Add(int x)
{
h[x]=max(h[x],dep[x]);
int y=h[x];
while(x)
{
h[x]=max(h[x],y);
if(!Ans[x]) Ans[x]=true,k--;
if(ls[fa[x]]==x&&!Ans[rs[fa[x]]]) if(rs[fa[x]]) MaxHeight[rs[fa[x]]]=max(MaxHeight[rs[fa[x]]],h[x]-1);
x=fa[x];
}
}
void Solve(int x)
{
if(Need(x)<=k) Add(x);
if(ls[x]&&rs[x])
{
if(MaxDep[ls[x]]<MaxHeight[x])
{
MaxHeight[rs[x]]=max(MaxHeight[rs[x]],MaxHeight[x]);
MaxHeight[ls[x]]=max(MaxHeight[ls[x]],MaxHeight[x]-1);
}
else
{
MaxHeight[ls[x]]=max(MaxHeight[ls[x]],MaxHeight[x]);
MaxHeight[rs[x]]=max(MaxHeight[rs[x]],MaxHeight[x]-1);
}
Solve(ls[x]); Solve(rs[x]);
}
else if(ls[x]) MaxHeight[ls[x]]=MaxHeight[x],Solve(ls[x]);
else if(rs[x]) MaxHeight[rs[x]]=MaxHeight[x],Solve(rs[x]);
}
template<typename T>void read(T &x)
{
T f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
x*=f;
}
int main() {
dp[1]=1,dp[2]=2;
for(int i=3;i<=40;i++) dp[i]=dp[i-1]+dp[i-2]+1;
read(n);read(k);
for(int i=1;i<=n;i++)
{
read(fa[i]);
if(~fa[i])
{
if(i<fa[i]) ls[fa[i]]=i;
if(i>fa[i]) rs[fa[i]]=i;
}
else rt=i,fa[i]=0;
}
dfs(rt);
Solve(rt);
for(int i=1;i<=n;i++) putchar(Ans[i]?'1':'0');
return 0;
}
