Burnside引理和Polya定理题集

本文版权归Azazel与博客园共有，欢迎转载，但需保留此声明，并给出原文地址，谢谢合作。

原文地址：https://www.cnblogs.com/Azazel/p/14964757.html

原文地址

Burnside引理和Polya定理单元测试

\(~~~~\) ~~不想做新题来水题解~~

A.The Colored Cubes

题意

\(~~~~\) 求给一个正方形的六个面涂上 \(n\) 种颜色的方案数。两种方案不同指两种方案之间不能通过旋转得到。

\(~~~~\) \(1\leq n< 1000\)

题解

\(~~~~\) 正方体关注点的置换：DIY Cube；

\(~~~~\) 正方体关注边的置换：Cubes；

\(~~~~\) 正方体关注面的置换：本题。

\(~~~~\) 具体方法如图：

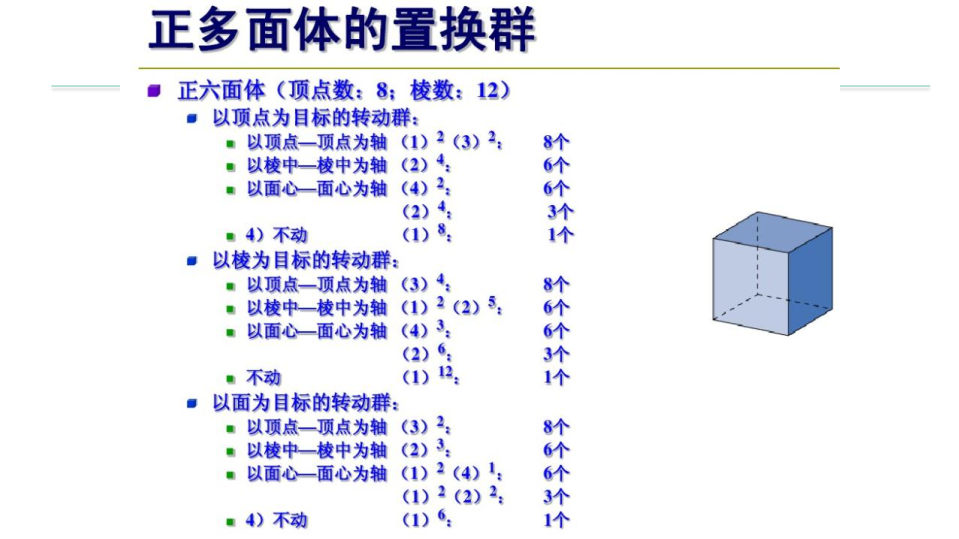
\(~~~~\) 然后直接套用 \(\texttt{P}\acute{o}\texttt{lya}\) 定理即可，得到答案为：

\[\dfrac{n^6+8n^2+12n^3+3n^4}{24} \]

代码

查看代码

#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
ll qpow(ll a,ll b)
{
	ll ret=1;
	while(b)
	{
		if(b&1) ret=ret*a;
		b>>=1;a=a*a;
	}
	return ret;
}
ll n;
int main() {
	while(scanf("%lld",&n)&&n)
		printf("%lld\n",(qpow(n,6)+8*qpow(n,2)+12*qpow(n,3)+3*qpow(n,4))/24);
	return 0;
}

B.Necklace

题意

\(~~~~\) 求使用 \(a\) 个白色，\(b\) 个灰色，\(c\) 个黑色珠子组成项链的本质不同方案数。两种方案若能通过旋转或翻转得到则本质相同。

\(~~~~\) \(3\leq a+b+c\leq 40\)

题解

\(~~~~\) ~~洛谷难度虚高。~~

\(~~~~\) 令 \(n=a+b+c\) ，考虑旋转的置换群的集合为 \(\{\text{旋转}0\text{位,}，\text{旋转}1\text{位,}，\dots \text{旋转}n-1\text{位,}\}\) ，则由模板题可知当旋转 \(k\) 位时，共有 \(\gcd(n,k)\) 个轮换，每个轮换内的 \(\dfrac{n}{\gcd(n,k)}\) 个珠子都必须是同色。由于有珠子数量的限制，不方便直接用\(\texttt{P}\acute{o}\texttt{lya}\) 定理，因此运用在 Pólya 定理学习笔记的 5.3 里面的套路，对珠子进行类似于背包的 DP 即可求解。

\(~~~~\) 然后考虑翻转操作的置换群的集合，此时需要将 \(n\) 分为奇数和偶数讨论：

当 \(n\) 为奇数时：对称轴必定只过一个点，此时的置换属于 \((1)^1(2)^{\frac{n-1}{2}}\) ，共 \(n\) 条这样的对称轴；
当 \(n\) 为偶数时：
- 对称轴过两个点，此时的置换属于 \((1)^2(2)^{\frac{n-2}{2}}\) ，共有 \(\frac{n}{2}\) 条这样的对称轴；
- 对称轴过两条边，此时的置换属于 \((2)^{\frac{n}{2}}\) ，共有 \(\frac{n}{2}\) 条这样的对称轴。

\(~~~~\) 综上，当有长为 \(1\) 的轮换与其他轮换复合时，枚举该轮换的珠子颜色，然后对剩下的轮换进行上面的 \(\texttt{DP}\) 即可，类似 Cubes 的套路。

代码

查看代码

#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
int a[5],tot,b[5];
ll dp[42][42][42],Ans=0;
int gcd(int a,int b){return b==0?a:gcd(b,a%b);}
ll Get(int d)
{
	for(int i=0;i<=a[1];i++) for(int j=0;j<=a[2];j++) for(int k=0;k<=a[3];k++) dp[i][j][k]=0;
	int other=tot/d;
	for(int i=1;i<=3;i++) if(a[i]%other) return 0;
	dp[0][0][0]=1;
	for(int i=1;i<=d;i++)
	{
		for(int j=a[1];j>=0;j--)
		{
			if(j%other) continue;
			for(int k=a[2];k>=0;k--)
			{
				if(k%other) continue;
				for(int l=a[3];l>=0;l--)
				{
					if(l%other) continue;
					if(j>=other) dp[j][k][l]+=dp[j-other][k][l];
					if(k>=other) dp[j][k][l]+=dp[j][k-other][l];
					if(l>=other) dp[j][k][l]+=dp[j][k][l-other];
				}
			}
		}
	}
	return dp[a[1]][a[2]][a[3]];
}
template<typename T>void read(T &x)
{
    T f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
    x*=f;
}
ll phi(ll n)
{
	ll ret=n;
	for(ll i=2;i*i<=n;i++)
	{
		if(n%i==0)
		{
			ret=ret/i*(i-1);
			while(n%i==0) n/=i;
		}
	}
	if(n>1) ret=ret/n*(n-1);
	return ret;
}
int main() {
	int T;
	read(T);
	while(T--)
	{
		Ans=0;
		read(a[1]);read(a[2]);read(a[3]);tot=a[1]+a[2]+a[3];
		for(int i=1;i*i<=tot;i++)
		{
			if(tot%i) continue;
			Ans+=Get(gcd(i,tot))*phi(tot/i);
			if(tot/i!=i) Ans+=Get(gcd(tot/i,tot))*phi(i);
		}
		if(tot&1)
		{
			ll tmp=0;
			for(int i=1;i<=3;i++)
			{
				if(a[i])
				{
					a[i]--;tot--;
					tmp+=Get(tot/2);
					a[i]++;tot++;
				}
			}
			Ans+=tmp*tot;
		}
		else
		{
			Ans+=(tot/2)*Get(tot/2);
			ll tmp=0;
			for(int i=1;i<=3;i++)
			{
				if(a[i])
				{
					tot--;a[i]--;
					for(int j=1;j<=3;j++)
					{
						if(a[j])
						{
							tot--;a[j]--;
							tmp+=Get(tot/2);
							tot++;a[j]++;
						}
					}
					tot++;a[i]++;
				}
			}
			Ans+=tmp*(tot/2);
		}
		printf("%lld\n",Ans/(tot<<1));
	}
	return 0;
}

C.Color

题意

\(~~~~\) 同洛谷模板题

题解

\(~~~~\) ~~卡常，恶心~~

\(~~~~\) 注意到给出的模数不一定是质数，甚至不一定与 \(n\) 互质，所以做快速幂的时候少乘一次即可。

\(~~~~\) 具体思路见 Pólya 定理学习笔记的 5.2

代码

查看代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
bool NotPrime[1000005];
int Prime[100005],cnt,MOD;
void makePrime(int N)
{
	NotPrime[0]=NotPrime[1]=true;
	for(int i=2;i<=N;i++)
	{
		if(!NotPrime[i]) Prime[++cnt]=i;
		for(int j=1;j<=cnt&&i*Prime[j]<=N;j++)
		{
			NotPrime[i*Prime[j]]=true;
			if(i%Prime[j]==0) break;
		}
	}
}
int qpow(ll a,int b)
{
	ll ret=1;
	while(b)
	{
		if(b&1) ret=ret*a%MOD;
		b>>=1;a=a*a%MOD;
	}
	return ret;
}
int phi(int n)
{
	int ret=n;
	for(int i=1;i<=cnt&&Prime[i]*Prime[i]<=n;i++)
	{
		if(n%Prime[i]==0)
		{
			ret=ret-ret/Prime[i];
			while(n%Prime[i]==0) n/=Prime[i];
		}
	}
	if(n>1) ret=ret-ret/n;
	return (ret%MOD+MOD)%MOD;
}
template<typename T>void read(T &x)
{
    T f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
    x*=f;
}
int main() {
	int T;
	read(T);
	makePrime(40000);
	while(T--)
	{
		ll Ans=0,n;
		read(n);read(MOD);
		for(ll i=1;i*i<=n;i++)
		{
			if(n%i) continue;
			Ans=(Ans+1ll*qpow(n,i-1)*phi(n/i)%MOD)%MOD;
			if(n/i!=i) Ans=(Ans+1ll*qpow(n,n/i-1)*phi(i)%MOD)%MOD;
		}
		printf("%lld\n",Ans);
	}
	return 0;
}

D.Birthday Toy

题意

\(~~~~\) \(n\) 个小珠子加一个大珠子，大珠子放在中间，小的围着它形成一个圆形并与之相邻，给所有珠子涂上 \(k\) 种颜色中的一种，在满足任意相邻珠子都不能同色的情况下的本质不同的涂色方案数是多少。两种方案若能通过旋转得到则本质相同，最后答案 \(\bmod 10^9+7\)。

\(~~~~\) \(1\leq n,k\leq 10^9\) 且至少 \(1000\) 组数据。

题解

\(~~~~\) 一看先给大珠子涂上一种颜色，然后删掉它和一种颜色，此时题目大致转化为 Pólya 定理学习笔记的 5.3 ，最后答案即为该题答案 \(\times k\) 。

\(~~~~\) 但本题的颜色数十分巨大，所以我们需要想办法规避用其开矩阵。我们发现本题若直接套用上述的题目，其转移矩阵的特点是初始时主对角线全部为 \(0\) ，其余全部为 \(1\) 。那么考虑对这个矩阵作若干次快速幂后的结果是否也有特点。

\(~~~~\) 手推或者写个程序找规律就会发现，对于大小为 \(m\times m\) 的矩阵 \(M\) 而言， \(M^d\) 其主对角线上所有数的值在 \(d\) 为奇数时等于 \(\frac{(m-1)^k-(m-1)}{m}\) ，偶数时等于 \(\frac{(m-1)^k+(m-1)}{m}\) ，而最后的主对角线总和 \(\times m\) 即可。

\(~~~~\) 然后我们就绕过了开超大矩阵的一步，其余就和上述题目没有区别了。

代码

查看代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
int n,m,K;ll Ans;
const int MOD=1000000007;
ll qpow(ll a,ll b)
{
	ll ret=1;
	while(b)
	{
		if(b&1) ret=ret*a%MOD;
		b>>=1;a=a*a%MOD;
	}
	return ret;
}
ll phi(ll n)
{
	ll ret=n;
	for(ll i=2;i*i<=n;i++)
	{
		if(n%i==0)
		{
			ret=ret/i*(i-1)%MOD;
			while(n%i==0) n/=i;
		}
	}
	if(n>1) ret=ret/n*(n-1)%MOD;
	return ret;
}
void Solve(int d)
{
	ll res;
	if(d&1) res=1ll*((qpow(m-1,d)-(m-1))%MOD+MOD)%MOD;
	else res=1ll*(qpow(m-1,d)+(m-1));
	Ans=(Ans+res%MOD*phi(n/d)%MOD)%MOD;
}
int main() {
	while(~scanf("%d %d",&n,&m))
	{
		Ans=0;m--;
		for(int g=1;g*g<=n;g++)
		{
			if(n%g) continue;
			Solve(g);
			if(n/g!=g) Solve(n/g);
		}
		Ans=Ans*qpow(n,MOD-2)%MOD*(m+1)%MOD;
		printf("%lld\n",Ans);
	} 
	return 0;
}

E.TRANSP - Transposing is Fun

题意

\(~~~~\) 求将 \(2^a\times 2^b\) 的矩阵变为其转置矩阵的最小交换次数。

\(~~~~\) \(1\leq a+b\leq 500000\)

题解

\(~~~~\) 首先需要搞懂转置矩阵是怎么变的~~（没错说的就是笔者这个搞错了的sb~~

\(~~~~\) 然后我们来举个 \(a=2,b=1\) 的例子，并且考虑到 \(2^a\) 和 \(2^b\) 如此特殊的编号，我们用二进制给行和列编号。

	00	01	10	11
0	\(1\)	\(2\)	\(3\)	\(4\)
1	\(5\)	\(6\)	\(7\)	\(8\)

\(~~~~\) 然后它会变为

	0	1
00	\(1\)	\(5\)
01	\(2\)	\(6\)
10	\(3\)	\(7\)
11	\(4\)	\(8\)

\(~~~~\) 随便挑几个数出来看： \(3:100\rightarrow010\) ，\(5:001\rightarrow100\)，\(6:011\rightarrow101\) 。

\(~~~~\) 不难发现，所有的数码都向右循环位移了 \(b\) 位/向左循环位移了 \(a\) 位。。

\(~~~~\) 然后我们来考虑本题，本题要求交换次数最少，若某个轮换内有 \(L\) 个数，那么显然该轮换内需要操作 \(L-1\) 次，因此本题我们要计算从原始状态到目标状态的置换里共有多少个轮换。~~（最优变计数，神神奇奇）~~

\(~~~~\) 因此本题可以化为这样一个问题：共有 \(a+b\) 个珠子要串成项链，每种珠子上涂两种颜色之一，规定向左旋转 \(a\) 位为同一项链，求共有多少种本质不同的方案。记上面转化成的问题答案为 \(Ans\) ，由于每种方案背后就对应了一种轮换，询问的答案就是 \(2^{a+b}-Ans\) 。

\(~~~~\) 然后我们考虑计算 \(Ans\) ，显然由重复过若干次的结论，每次置换时共有 \(\gcd(a,a+b)=\gcd(a,b)\) 个轮换，每个轮换有 \(\frac{a+b}{\gcd(a,b)}\) 个点。考虑旋转 \(a\) 位肯定不好求，所以我们把每个轮换按标号排序依次的第 \(1\) 个点缩为一个点，这个点内部的染色方案就是 \(2^{\gcd(a,b)}\) ，以此类推，这样就变成用 \(2^{\gcd(a,b)}\) 种颜色染 \(\frac{a+b}{\gcd(a,b)}\) 个点，本质相同表示可以用旋转得到，然后就变成裸题了。

\(~~~~\) 最后原问题的答案就是：

\[\large 2^{a+b}-\dfrac{\sum_{d|n} 2^{\gcd(a,b)d}\times \varphi(\dfrac{n}{d})}{n} \]

代码

查看代码

#include <cstdio>
#include <algorithm>
using namespace std;
#define ll long long
const int MOD=1000003;
ll T,a,b,n,Ans=0;
ll qpow(ll a,ll b)
{
	ll ret=1;
	while(b)
	{
		if(b&1) ret=ret*a%MOD;
		b>>=1;a=a*a%MOD;
	}
	return ret;
}
int gcd(int a,int b){return b==0?a:gcd(b,a%b);}
ll phi(ll n)
{
	ll ret=n;
	for(int i=2;i*i<=n;i++)
	{
		if(n%i) continue;
		ret=ret*qpow(i,MOD-2)%MOD*(i-1)%MOD;
		while(n%i==0) n/=i;
	}
	if(n>1) ret=ret*qpow(n,MOD-2)%MOD*(n-1)%MOD;
	return ret;
}
void Solve(int i)
{
	Ans+=qpow(2,i*gcd(a,b))*phi(n/i)%MOD;Ans%=MOD;
}
int main() {
	scanf("%d",&T);
	while(T--)
	{
		Ans=0;
		scanf("%lld %lld",&a,&b);
		n=(a+b)/gcd(a,b);
		for(int i=1;i*i<=n;i++)
		{
			if(n%i) continue;
			Solve(i);if(n/i!=i) Solve(n/i);
		}
		printf("%lld\n",((qpow(2,a+b)-Ans*qpow(n,MOD-2)%MOD)%MOD+MOD)%MOD);
	}
	return 0;
}

F.Isomorphism（神仙题）

题意

\(~~~~\) 求 \(n\) 个点，\(m\) 种颜色染一幅无向完全图的本质不同方案数。两种方案本质相同定义为可以通过点重新标号得到。

\(~~~~\) \(1\leq n\leq 53,1\leq m\leq 1000\)

题解

\(~~~~\) 神仙题+论文题~~（不看题解就不会~~

\(~~~~\) 考虑到边的置换并不好求，所以我们来试着找边与点的置换的关系：

\(~~~~\) 一条边不同也仅当其两个端点不同，因此我们来考虑一条边两个端点的关系：

若两个端点在同一轮换：假设该轮换的大小为 \(L\) ，则这样的边共有 \(\dfrac{L\times(L-1)}{2}\) 条：
- 若 \(L\) 为奇数，由于一个置换本身有 \(L\) 条边，所以最后只会有 \(\dfrac{\frac{L(L-1)}{2}}{L}=\dfrac{L-1}{2}\) 条边；
- 若 \(L\) 为偶数，当两端点相隔刚好为 \(\dfrac{L}{2}\) 时，循环中只有 \(\dfrac{L}{2}\) 条边，否则有 \(L\) 条，所以最后有 \(\dfrac{\frac{L(L-1)}{2}-\frac{L}{2}}{2}=\dfrac{L}{2}\) 条边.

\(~~~~\) 综上，大小为 \(L\) 的点循环可以造成 \(\lfloor \frac{L}{2} \rfloor\) 个边循环,然后再来考虑两个端点分别在长为 \(L_1,L_2\) 的轮换当中，显然共有 \(L_1\times L_2\) 条边，但其中 \(\operatorname{lcm}(L_1,L_2)\) 次就会有循环，所以总共有 \(\dfrac{L1\times L_2}{\operatorname{lcm}(L_1,L_2)}=\gcd(L_1,L_2)\) 个边轮换。

\(~~~~\) 知道了点轮换的大小与边轮换的关系，因此自然想到求所有点轮换的大小，我们知道所有点轮换阶的大小的和就是 \(n\) ，而且 \(n\) 很小，因此可以用 \(\texttt{dfs}\) 枚举。

\(~~~~\) 若共有 \(k\) 个点轮换，大小分别为 \(L_1,L_2,\dots,L_k\) ，然后我们可以知道边的轮换个数为：

\[\sum_{i=1}^k \lfloor \frac{L_i}{2} \rfloor+\sum_{i=1}^k\sum_{j=1}^{i-1}\gcd(L_i,L_j) \]

\(~~~~\) 下面我们把这个东西记作 \(c\) ，其实它应该是关于 \(\{L\}\) 的函数。

\(~~~~\) 但是，我们还没有确定每个点填进哪个点轮换，不考虑其他限制，则方案数为 \(\dfrac{n!}{\prod_{i=1}^k L_i!}\) （轮换内部先取消顺序），但是事实上除去每个轮换的第一个点，其他点的顺序是会使得整个轮换的积对应不同置换的，因此再乘上 \(\prod_{i=1}^k (L_i-1)!\) 。

\(~~~~\) 最后，若干个大小相等的点轮换之间会产生重复，因此若大小为 \(L\) 的点轮换有 \(B_L\) 个，则还要去除掉 \(B_L!\) 种中的重复。

\(~~~~\) 然后就做完了这道题。

代码

查看代码

#include <cstdio>
#include <algorithm>
using namespace std;
#define ll long long
ll n,m,MOD,L[105],fac[105],Ans,Inv[105],Inv2[105],g[55][55],Pow[250005];
ll qpow(ll a,ll b)
{
	ll ret=1;
	while(b)
	{
		if(b&1) ret=ret*a%MOD;
		b>>=1;a=a*a%MOD;
	}
	return ret;
}
void Solve(int K)
{
	ll tmp=0,C=0,S=fac[n];
	for(int i=1;i<=K;i++)
	{
		tmp++;
		if(i==K||L[i]!=L[i+1]) S=S*Inv2[tmp]%MOD,tmp=0;
		C=(C+L[i]/2)%MOD;S=S*Inv[L[i]]%MOD;
		for(int j=1;j<i;j++) C=(C+g[L[j]][L[i]])%MOD;
	}
	Ans=(Ans+S*Pow[C]%MOD)%MOD;
}
void dfs(int K,ll lst,ll Sum)
{
	if(!Sum)
	{
		Solve(K-1);
		return;
	}
	for(int i=min(lst,Sum);i>=1;i--)
	{
		L[K]=i;
		dfs(K+1,i,Sum-i);	
	}
}
int main() {
	scanf("%lld %lld %lld",&n,&m,&MOD);fac[0]=fac[1]=1;Inv[1]=1;Pow[0]=1;
	for(int i=1;i<=n*n/2;i++) Pow[i]=Pow[i-1]*m%MOD;
	for(int i=0;i<=n;i++) g[i][0]=i;
	for(int i=0;i<=n;i++) for(int j=1;j<=i;j++)	g[i][j]=g[j][i%j];
	for(int i=2;i<=n;i++) fac[i]=fac[i-1]*i%MOD,Inv[i]=MOD-(MOD/i)*Inv[MOD%i]%MOD;
//	for(int i=1;i<=n*n/2;i++) printf("%lld ",fac[i]);
	Inv2[n]=qpow(fac[n],MOD-2);
	for(int i=n-1;i>=0;i--) Inv2[i]=Inv2[i+1]*(i+1)%MOD;
	dfs(1,n,n);
	printf("%lld",Ans*Inv2[n]%MOD);
	return 0;
}

\(~~~~\) ~~在本博客中挂了那么多次学习笔记的链接不去看看真的好吗~~

posted @ 2021-07-02 20:15 Azazеl 阅读(308) 评论(0) 编辑收藏举报

刷新页面返回顶部

Azazel

Burnside引理和Polya定理题集

Burnside引理和Polya定理单元测试

A.The Colored Cubes

题意

题解

代码

B.Necklace

题意

题解

代码

C.Color

题意

题解

代码

D.Birthday Toy

题意

题解

代码

E.TRANSP - Transposing is Fun

题意

题解

代码

F.Isomorphism（神仙题）

题意

题解

代码

公告