Pólya 定理学习笔记
Pólya 定理学习笔记
\(~~~~\) 已经不认识 群 和 换 了/dk
\(\S 1.\)群
\(~~~~\) 给定一个集合 \(G\) 和集合内的运算 \(\circ\) ,若 \(G\) 和 \(\circ\) 满足:
-
封闭性:\(\forall a,b\in G\),\(a \circ b\in G\) ;(即任意两个集合中的元素的运算结果仍在集合中)
-
结合律:\(\forall a,b,c\in G\),\((a \circ b)\circ c=a\circ(b \circ c)\);(即在连续运算时其先后顺序对结果没有影响)
-
存在单位元:\(\exist e\in G,\text{s.t.} \forall a\in G,e\circ a=a \circ e=a\) ;(即存在单位元,其与任何其他元素运算的结果均为该元素本身)
-
存在逆元,\(\forall a\in G,\exist b\in G,\text{s.t.} a \circ b=e\) ,可将 \(b\) 记作 \(a^{-1}\)。(即对于任意元素都有元素与之进行运算和结果为单位元)
\(~~~~\) 此时上述集合 \(G\) 和运算 \(\circ\) 一并称为群,记作 \((G,\circ)\),比如 \((\Bbb{Z},+),(\Bbb{R},\times)\) 都是群( \(+\) 和 \(\times\) 这里都是对于数的运算)
\(\S2.\) 置换群
$\S 2.1 $置换
\(~~~~\) 置换简单来说就是一个集合映射到自身的双射。
(双射:同时满足单射和满射的映射;单射:在映射\(f:A\rightarrow B\) 中,满足 \(\forall x,y\in A\),若 \(x\not = y\) ,则 \(f(x)\not = f(y)\) 的映射;满射:在映射 \(f:A\rightarrow B\) 中,满足 \(\forall y\in B\) ,\(\exist x\in A,\text{s.t.}f(x)=y\) 的映射)
\(~~~~\) 此时可将一个置换简记为:
\(~~~~\) 由上述定义可知:\(\{b\}\) 是 \(\{a\}\) 的一个排列,因此对于一个集合 \(M\),其置换的数量为 \(|M|!\) ,此时的置换称为 \(\pmb{|M|}\) 元置换。
\(~~~~\) 同时,置换:
\(~~~~\) 被称为 \(n\) 元恒等置换。
\(\S2.2\) 置换乘法
\(~~~~\) 置换乘法按照从左到右的顺序,即置换 \(\sigma\tau(a_i)=\tau(\sigma(a_i))\) 。
\(~~~~\) 因此,置换乘法满足结合律:
\(~~~~\) 设:有 \(n\) 元置换 \(\sigma,\tau,\rho\)
\(~~~~\) 则 \((\sigma\tau)\rho(a_i)=\rho\{\tau[\sigma(a_i)]\}\) ,\(\sigma(\tau\rho)(a_i)=(\tau\rho)[\sigma(a_i)]=\rho\{\tau[\sigma(a_i)]\} (i\in [1,n])\) 故两者相等。
\(\S2.3\) 置换群
\(~~~~\) 令 \(G\) 表示在集合 \(M\) 下所有 \(n\) 元置换组成的集合,则 \(G\) 连同置换乘法可组成一个群,将其称为置换群。
\(~~~~\) 证明:
- 封闭性:对于置换 \(\sigma,\tau\in G\) ,\(\sigma\tau\) 显然也是 \(G\) 中的一个 \(n\) 元置换;
- 结合律:见
2.2置换乘法中的证明; - 存在单位元:\(n\) 元恒等置换即为单位元;
- 存在逆元:对于任意置换 \(\sigma=\begin{pmatrix} a_1&a_2&\dots&a_n\\ b_1&b_2&\dots&b_n \end{pmatrix}\),存在置换\(\sigma^{-1}=\begin{pmatrix} b_1&b_2&\dots&b_n\\ a_1&a_2&\dots&a_n \end{pmatrix}\) 使得 \(\sigma \sigma^{-1}\) 为 \(n\) 元恒等置换。
\(~~~~\) 一般将 \(n\) 元置换的群记作 \(s_n\) 。
\(\S3.\) 轮换
\(\S3.1\) 轮换
\(~~~~\) 轮换,也被称作循环,可用于简记置换。将长度为 \(m\) 的,满足如下形式的置换可进行简记:
\(~~~~\) 若两个轮换中不存在相同的元素,则称这两个轮换是不相交的。显然,一个置换可以被唯一地表示为若干不相交轮换的积(不考虑轮换中元素的次序和轮换的次序)。
\(\S3.2\) 轮换指标
\(~~~~\) 由 3.1 可知,任意 \(S_n\) 中的置换 \(\sigma\) 都可以唯一分解为若干不相交轮换的积,即:
\(~~~~\) 记 \(C_i(\sigma)\) 表示置换 \(\sigma\) 中长为 \(i\) 的轮换出现的次数,并用 \((i)^{C_i(\sigma)}\) 表示,则所有 \(S_n\) 中的置换 \(\sigma\) 都可以用:
\(~~~~\) 来表示。显然,一部分置换在上述表示下是完全相同的,此时我们将所有可以用同一个上述形式式子表示的置换归为一个共轭类。如:\((1,2)(3,4)\) 和 \((1,3)(2,4)\) 就属于同一个共轭类。
\(~~~~\) 同时这里不会加证明地给出一个结论,\((1)^{C_1(\sigma)}(2)^{C_2(\sigma)}\dots(m)^{C_m(\sigma)}\) 共轭类的元素个数为:
\(~~~~\) 由此可以定义轮换指标,设 \(x_1,x_2,\dots,x_n\) 为 \(n\) 个未定元,\(G\) 为 \(S_n\) 的置换集合,则轮换指标 \(P_G\) 的定义为:
\(~~~~\) 比如:
\(\S4.\text{Burnside}\) 引理
\(\S4.1\) 等价类/轨道
\(~~~~\) 如图:
\(~~~~\) 对于一个置换群,若对某点进行若干次操作,它都只能变为一些特定的值,则这些元素的集合即为一个等价类,也就是它们在同一轨道上。
\(~~~~\) 比如上图中的 \(1\) 只能变化到 \(1\) 和 \(3\) ,同理 \(2\) 只能变化到 \(2\) 和 \(4\) ,因此上面的置换群有两个等价类 \(\{1,3\}\) 和 \(\{2,4\}\) ,将 \(k\) 所在的等价类记为 \(E_k\)。
\(\S4.2\ k\)不动置换群
\(~~~~\) \(k\) 不动置换群即对于 \(k\in[1,n]\) ,所有使得 \(k\) 保持不变的置换的集合,将其记为 \(Z_k\) 。
\(~~~~\) 此外再不会加证明地给出 轨道-稳定子定理:\(|E_k||Z_k|=|G|,k\in[1,n]\)
\(\S4.3\ \text{Burnside}\) 引理
\(~~~~\) 令 \(G\) 是 \(X=[1,n]\) 上的一个置换群,则 \(G\) 在 \(X\) 上的等价类共有:
\(~~~~\) 其中 \(c_1(\sigma)\) 即置换 \(\sigma\) 拆分成的若干轮换的积中长为 \(1\) 的轮换的个数。
\(\S 5.\text{P}\acute{o}\text{lya}\) 定理
\(\S 5.1.\text{P}\acute{o}\text{lya}\) 定理
\(~~~~\) 由于 \(\text{Burnside}\) 定理需要枚举所有不动点数目,这在时间复杂度上难以接受(\(n^m\)) ,所以我们需要一种快速计算不动点数目的方法。
\(~~~~\) 我们可以把对于集合 \([1,n]\) 的所有置换看成是对集合中所有元素染为 \(m\) 种色,则当若干元素(注意并不一定是全部)染为同种颜色且它们在同一个轮换内时它们都是不动点。那么同理,若一个置换有 \(k\) 个轮换,则每个轮换都有 \(m\) 种颜色选择,则因此该置换共有 \(m^k\) 个不动点。
\(~~~~\) 综上,可以写出经过该定理优化后的式子:
\(~~~~\) 其中 \(a_i\) 是一个 \(n\) 元置换, \(k_\sigma\) 表示该置换展开为轮换的积后的轮换个数。
\(\S5.2.\) 模板题
题意
\(~~~~\) 给定一个 \(n\) 个点,\(n\) 条边的环,有 \(n\) 种颜色,给每个顶点染色,问有多少种本质不同的染色方案,答案对 \(10^9+7\) 取模
\(~~~~\) 注意本题的本质不同,定义为:只需要不能通过旋转与别的染色方案相同。
\(~~~~\) 题目传送门
题解
\(~~~~\) 定义本题的置换群的 \(G\) 为 \(\{\text{rotate0位,rotate1位,rotate2位},\dots,\text{rotate n-1位} \}\) 。
\(~~~~\) 则显然对于置换 \(\sigma\) ,若含义为旋转 \(k\) 位,则其轮换数为 \(\gcd(n,k)\) 。这点稍加证明:对于旋转 \(k\) 位,若不动点在一个长为 \(a\) 的循环节上, 则 \(a\) 首先定然能满足 \(a|n\) ,即 \(a\) 能完全覆盖整个串;其次 \(a\) 也一定能满足 \(a|k\),因为 \(a\) 必须也能刚好覆盖一次 \(k\) ,综上,\(a\) 应该为 \(n\) 和 \(k\) 的公约数,因此有 \(a=\gcd(n,k)\) 时,需要依次覆盖 \(a\) 上的所有点,故共有 \(a\) 个轮换。
\(~~~~\) 然后我们把这带入上面Pólya定理的式子得到:
\(~~~~\) 然后套路地开始化式子:
\(~~~~\) 到这里理论上单次询问是 \(\sqrt n\times \sqrt n\) (枚举因数,每次找 \(\varphi\) ),但是由于计算 \(\varphi\) 时是算的因数,所以我们信仰过掉实际的单次时间复杂度是 \(n^\frac{3}{4}\) 。
\(\S5.3.\) 只能使用 \(\text{Burnside}\) 引理的情况
题意
\(~~~~\) \(n\) 个点 \(m\) 种颜色的手链,求其中有 \(k\) 对颜色不能相邻的本质不同的手环数。(本质不同的定义是旋转后不同)
\(~~~~\) \(1\leq n\leq 10^9,1\leq m\leq 10,1\leq k\leq \dfrac{m(m-1)}{2}\) .
\(~~~~\) 题目传送门
题解
\(~~~~\) 由于颜色不相邻并不好定义出对应的方便计算轮换数量的置换群,而且本题 \(m\) 极小,我们可以考虑直接用 \(\text{Burnside}\) 引理。
\(~~~~\) 那么仍然考虑当前旋转的位置,若现在旋转 \(k\) 个位置,由 \(\S5.2\) 里面的分析可知共有 \(\gcd(k,n)\) 个轮换,而每个轮换的元素个数是相等的,因此每个轮换有 \(\dfrac{n}{\gcd(k,n)}\) 个点,而且也可知道此时最小的循环节就是 \(\gcd(k,n)\) ,因此每个轮换中相邻的两个点的距离也是 \(\gcd(k,n)\) 。
\(~~~~\) 因此我们可以把所有点按下图分类:(为什么它看起来是歪的
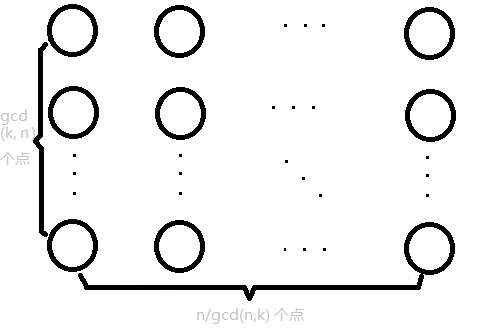
\(~~~~\) 每一列的点都可以认为是 \([x,x+\gcd(n,k)-1]\) 内的所有点,而每一行的点都是原有的轮换上的点。
\(~~~~\) 显然为了使得该轮换能满足整个方案为不动点,每个轮换上的点必须染为同色,即上图中同一行的点必须染为同色。
\(~~~~\) 再来考虑相邻点之间的限制,我们可以这样修改原来的连边方式:
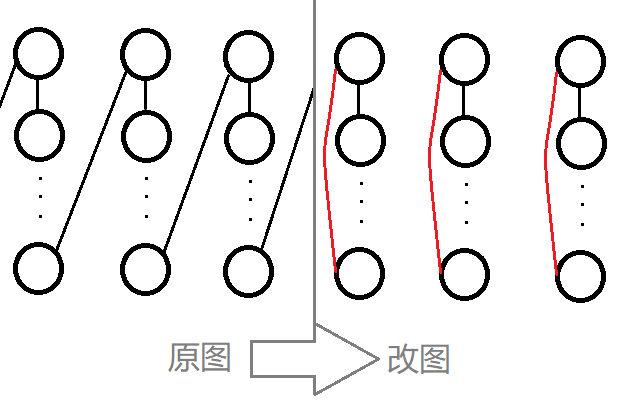
\(~~~~\) 改完过后的图相当于把图改为若干长 \(\gcd(k,n)\) 的小环。 显然,由于同一行的点颜色相同,因此两图在考虑相邻点颜色时是相同的,但此时我们可以更简单地求出答案,因为在修改后的图中,确定一个小环的答案相对简单,并且不用考虑一个轮换内颜色相同的限制。
\(~~~~\) 那么如何求出一个小环的答案呢?定义 \(dp_{i,j}\) (\(0\leq i\leq \gcd(k,n),1\leq j\leq m\))表示现在考虑到环上第 \(i\) 个点,其染成颜色 \(j\) 的答案。此时把第 \(\gcd(k,n)\) 个点拆成 \(0\) 和 \(\gcd(k,n)\) ,枚举 \(0\) 号点的涂色,然后大力转移即可: \(dp_{i,j}\sum_{k=1}^j dp_{i-1,k}\times p_{j,k}\) ,其中 \(p_{i,j}\in\{0,1\}\) 表示 \(i\) 和 \(j\) 能否相邻,若能则为 \(1\) ,否则为 \(0\)。然而这个 \(\texttt{dp}\) 还是 \(\mathcal{O(\gcd(n,k)m)}\) 的,可以被卡掉,所以我们需要一些优化。显然,这种只与前面有关的 \(\texttt{dp}\) 可以用矩阵快速幂优化,所以直接上矩阵:
\(~~~~\) 然后 \(\texttt{dp}\) 的时间复杂度就到了 \(m^3 \log \gcd(n,k)\) 。
\(~~~~\) 最后是统计所有的答案,还是沿用上面的套路,令刚刚矩阵快速幂的初始矩阵为 \(F\) ,转移矩阵为 \(M\) ,则(大家都知道最后是矩阵第一列求和):
\(~~~~\) 所以这题就以 \(\mathcal{O(n^{\frac{3}{4}}\times m^3 \log d)}\) 的信仰复杂度过掉。
代码
查看代码
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
int n,m,K;ll Ans;
const int MOD=9973;
struct Matrix{
ll A[11][11];
Matrix(){memset(A,0,sizeof(A));}
void Init(){memset(A,0,sizeof(A));}
}e,M;
ll qpow(ll a,ll b)
{
ll ret=1;
while(b)
{
if(b&1) ret=ret*a%MOD;
b>>=1;a=a*a%MOD;
}
return ret;
}
ll phi(ll n)
{
ll ret=n;
for(ll i=2;i*i<=n;i++)
{
if(n%i==0)
{
ret=ret*qpow(i,MOD-2)%MOD*(i-1)%MOD;
while(n%i==0) n/=i;
}
}
if(n>1) ret=ret*qpow(n,MOD-2)%MOD*(n-1)%MOD;
return ret;
}
Matrix Mul(Matrix x,Matrix y)
{
Matrix ret;
for(int i=1;i<=m;i++)
for(int j=1;j<=m;j++)
for(int k=1;k<=m;k++) ret.A[i][j]=(ret.A[i][j]+x.A[i][k]*y.A[k][j]%MOD)%MOD;
return ret;
}
Matrix Matrixqpow(Matrix a,ll b)
{
Matrix ret=e;
while(b)
{
if(b&1) ret=Mul(a,ret);
b>>=1;a=Mul(a,a);
}
return ret;
}
void Solve(int d)
{
ll Tmp=0;
Matrix res=Matrixqpow(M,d);
for(int i=1;i<=m;i++) Tmp+=res.A[i][i];
Ans=Ans+Tmp*phi(n/d);
}
template<typename T>void read(T &x)
{
T f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
x*=f;
}
int main() {
int T;read(T);
while(T--)
{
Ans=0;read(n);read(m);read(K);
for(int i=1;i<=m;i++)
{
e.A[i][i]=1;
for(int j=1;j<=m;j++) M.A[i][j]=1;
}
for(int i=1,a,b;i<=K;i++)
{
read(a);read(b);
M.A[a][b]=M.A[b][a]=0;
}
for(int g=1;g*g<=n;g++)
{
if(n%g) continue;
Solve(g);if(n/g!=g) Solve(n/g);
}
printf("%lld\n",Ans*qpow(n,MOD-2)%MOD);
}
return 0;
}

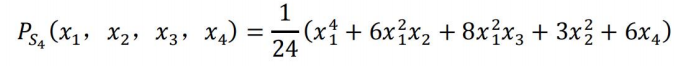


 浙公网安备 33010602011771号
浙公网安备 33010602011771号