构造

Even Degrees

题意

\(~~~~\) 给出一张 \(n\) 个点 \(m\) 条边的无向简单连通图，给每一条边定向，使得每一个点出度为偶数，输出任意一种方案，或者说明无解。

---

题解

\(~~~~\) 不难想到，当 \(m\) 为奇数时，由于每条边都会有 \(1\) 的出度贡献，故一定会有一个点其出度为奇数，此时无解。

\(~~~~\) 然后，我们只关心每个点出度的奇偶性，不妨按输入的方向先将图转化为有向图，然后进行调整。将所有出度为奇数的点提出来。

\(~~~~\) 此时，改变原图的某一条边 \((u_i,v_i)\) 的方向，就相当于让 \(u_i\) 的度 \(-1\) ，\(v_i\) 的度 \(+1\) 。如上所述，我们只关心每个点出度的奇偶性，因此 \(-1\) 和 \(+1\) 相对于奇偶性是等价的，不妨把操作都转化为 \(\operatorname{xor} 1\) 。因此改变某条边的方向就是将这条边两个端点的权值 \(\operatorname{xor} 1\) 。不难发现，这样的操作进行偶数次是无意义的，也就是说进行偶数次就相当于不调整方向。

\(~~~~\) 现在来考虑如何调整，我们发现对于一条路径，改变路径上所有的边，只会影响这条路径的两个端点的权值，因此直接将任意两个权值为 \(1\) 的点路径上的所有边全部进行一次操作即可。由于奇数权值的点在合法的前提下一定只有偶数个，因此不存在剩余单独一个点的情况。

\(~~~~\) 当然进行上述的操作时，如果用 DFS/BFS 会达到 \(\Theta(n^2)\) 的复杂度，因此考虑建出原图的一个生成树，然后对于每次操作进行树上差分。最后对于每条边，若为树边，根据操作次数进行判断；若为非树边，由于原图联通，故我们生成的一定是树而不是森林，那么非树边一定不会被经过，按原序输出即可。

---

Skolem XOR Tree

题意

---

题解

\(~~~~\) 先来看怎么判无解，由于对应两个点权值相同，因此这条路径上的点除去这两个对应点后的异或和仍然是这两个数的权值，所以不难想到当 \(n\) 为 \(2\) 的幂时，你无法用除去 \(n\) 的其他点构造出二进制下最高位为 \(1\) ，此时就是无解的情况。

\(~~~~\) 然后怎么利用一些异或的性质呢？由于 \(1\) 是在异或中比较万能的一个数，我们来考虑怎么充分利用 \(1\)，不难想到将奇数和偶数分为一组，然后按下图连边

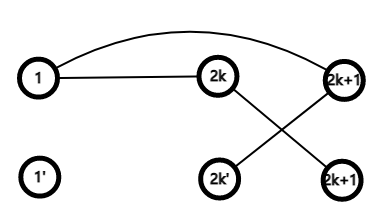
\(~~~~\) 这样分组，\(1 \oplus 2k = 2k+1,1 \oplus 2k+1 =2k\) ，因此是满足条件的。

\(~~~~\) 至于 \(1\) 的时候，由于 \(2k \oplus 2k+1=1\) ，因此把 \(1'\) 与随便一个下面的点连起来即可。

\(~~~~\) 那么难点就在于如何处理 \(n\) 为偶数的情况 ，即 \(n\) 不能被分在某一组内。此时我们要用两条边将 \(n\) , \(n'\) 分别连接至一个上面和下面的点，使得这两个点之间的路径上的点异或和为 \(n\) ，那么 \(1\) 在此时也一定会作为一个枢纽，因此一个思路是异或掉 \(n\) 的二进制下的某一个 \(1\) ，然后找到其他位所对应的点。由于有之前组内构造时的性质：从某个点出发到达自己的对应点的异或和为自身，那么除掉这个点后异或和就为 \(0\) 。但要注意我们还会经过 \(1\) ，因此最方便的做法是异或掉 \(n\) 在二进制下最后一位 \(1\)（即异或 \(\operatorname{lowbit(n)}\)） ，然后连接到 \(1\) 后再将 \(n\oplus \operatorname{lowbit}(n) \oplus 1'\) 连接到 \(n'\) 。此时之间的路径一定满足条件。