五岔路口交通问题

前言

五岔路口交通问题是已经给定了道路的通行情况，我们可以直接分析得到所有合法的道路通行方式，然后根据这些再得到不同方式之间的通行关系

---

建图过程

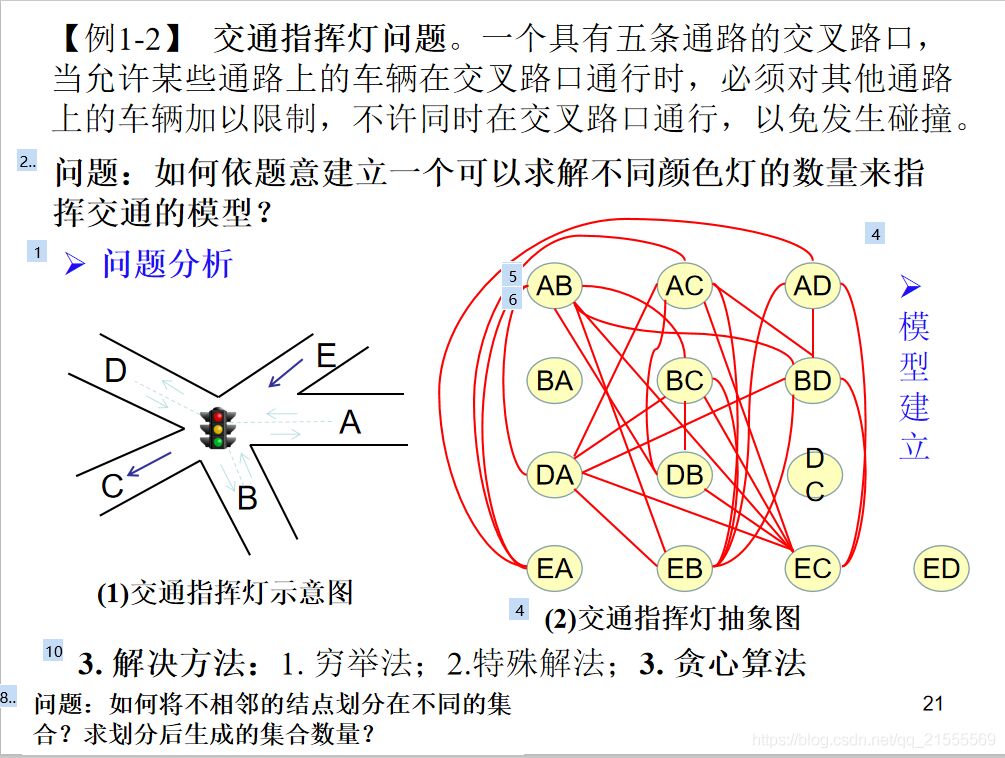
建点

如图

E为入口，是单行道;

C为出口，是单行道；

其余都为双行道，也就是可以作入口，也可以当出口

1. E作为入口，可以将其余4个作为出口，4种方式
2. C作为出口，除了E外有3个作为入口，3种方式
3. 其余3个，既可以作出口，也可以作为入口，它们相互之间有6种方式

共13种
每个点，表示为一种通行方式

建边

手动模拟，两种方式可以同时通行的条件是两道路不相交。

注意！

双行道是右侧车道为出，左侧为入。

则我们可以用邻接矩阵的方式表示这个条件：

若边权为1，则表示两条道路有冲突，边权为0，表示无冲突

---

贪心算法

1. 将顶点按度数从大到小排序
2. 将未被染色且度数最大点染色，然后将其他与它不相连的点染为相同颜色
3. 若仍存在未染色的点，则增加新的颜色染色，然后重复2，3；

---

代码

点击查看代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

struct Node
{
	char road[8];
	int color;
	int deg;
};

Node v[13] = {
	{"ED",0}, {"AC",0}, {"AD",0}, {"BA",0}, {"BC",0},
	{"BD",0}, {"DA",0}, {"DB",0}, {"DC",0}, {"EA",0},
	{ "EB",0},{"EC",0},{ "AB", 0}//通路与染色编号
};
bool e[13][13] = {
					{0,0,0,0,0,0,0,0,0,0,0,0,0},
					{0,0,0,0,0,1,1,1,0,0,1,1,0},
					{0,0,0,0,0,1,0,0,0,1,1,1,0},
					{0,0,0,0,0,0,0,0,0,0,0,0,0},
					{0,0,0,0,0,0,1,1,0,0,1,1,1},
					{0,1,1,0,0,0,1,0,0,0,1,1,1},
					{0,1,0,0,1,1,0,0,0,0,1,1,1},
					{0,1,0,0,1,0,0,0,0,0,0,1,1},
					{0,0,0,0,0,0,0,0,0,0,0,0,0},
					{0,0,1,0,0,0,0,0,0,0,0,0,1},
					{0,1,1,0,1,1,1,0,0,0,0,0,1},
					{0,1,1,0,1,1,1,1,0,0,0,0,1},
					{0,0,0,0,1,1,1,1,0,1,1,1,0}
				};//邻接矩阵

void deg_solve()
{
	for(int i = 0; i < 13; i ++ )//求出度数
	{
		int sum = 0;
		for(int j = 0; j < 13; j ++ )
		{
			sum += e[i][j];
		}
		v[i].deg = sum;
	}
	/* 冒泡排序 */
	for(int i = 0; i < 13; i ++ )
	{
		for(int j = 0; j < 13; j ++ )
		{
			if(v[i].deg < v[j].deg)
			{
				swap(v[i], v[j]);

				for(int k = 0; k < 13; k ++ )
				{
					swap(e[i][k], e[j][k]);
					swap(e[k][i], e[k][j]);
				}
			}
		}
	}
}
int main()
{
	int cnt_color = 0;
	
	//deg_solve();
	/*排序后并不会得到更好的结果*/
	
	for (int i = 0; i < 13; i ++)
	{
		if (v[i].color == 0)//未被涂色
		{
			bool flag = true;
			v[i].color = ++ cnt_color;
			for (int j = 0; j < 13; j ++)
			{
				if (v[j].color != 0) continue;
				if (e[i][j] == 0)//无冲突且无染色
				{
					for (int k = 0; k < 13; k ++)
					{
						if (e[j][k] == 1 && v[k].color == v[i].color)//j与和i相同颜色的点相邻
						{
							flag = false;
						}
					}

					if (flag)//找出
					{
						v[j].color = cnt_color;
					}
				}
			}
		}
	}		
	
	for(int i = 1; i <= cnt_color; i ++ )
	{
		printf("color %d : ", i);
		for(int j = 0; j < 13; j ++ )
		{
			if(v[j].color == i)
			{
				printf("%5s",v[j].road);
			}
		}
		printf("\n");
	}

	for (auto x : v)
	{
		printf("%s\t", x.road);
	}
	printf("\n");
	for (auto x : v)
	{
		printf("%d\t", x.color);
	}
}

参考博客

数据结构：五岔路口交通管理红绿灯设计

数据结构：五岔路口交通灯问题

---

后记

关于这个问题，留下的问题是如何仅靠道路的通行情况，来让程序自己建图