【cf补题记录】Codeforces Round #614 (Div. 2)
这场感觉挺简单...因为我会做D题......
A
题意:有n层楼,有个人在第s层,其中,每层楼都有一个吃饭的地方,但现在有k层楼是不能吃饭。问这个人从第s层出发,至少要走多少层才能吃到饭。
题解:因为n的范围是2~1e9,所以不能建一个bool值表O(1)的速度判断第i层是否可以用餐;另外k的范围是1 ~ min(n-1, 1000),即k的最大值是1000;所以即便第s层在这k层里的中间位置,向低层或者高层延申最多也只需要走(总共)1000层,同时,因为要判断该层是否可以用餐需要查询该层是否包含在这k层里,所以时间复杂度是O(\(k^2\)),即1e6——不用优化就可以过了。
// https://codeforces.com/contest/1293/problem/A
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int T, n, s, k;
int a[1003];
int main()
{
scanf("%d", &T);
while(T--){
scanf("%d %d %d", &n, &s, &k);
for(int i = 0; i < k; i++) scanf("%d", &a[i]);
// O(k^2)
int l, r, i, ans = 0;
l = r = s;
while(true){
if(l > 0){ // 向底层走
for(i = 0; i < k; i++){
if(a[i] == l) {
l--;
break;
}
}
if(i == k) break; // 若 i == k, 则第i层可以用餐
}
if(r <= n){ // 往高层走
for(i = 0; i < k; i++){
if(a[i] == r){
r++;
break;
}
}
if(i == k) break; // 同上
}
ans++;
}
printf("%d\n", ans);
}
return 0;
B
题意:有n个人参加比赛,其中有个bug选手JOE每道题都会答对,而且每当有t人(一次机会)答错出局时,选手JOE就会得到 \(\frac{t}{s}\) 的奖金(s代表的是当前还在答题的选手(不包括JOE))——即原本有n人答题,第一次淘汰了\(t_1\)人,第二次淘汰了\(t_2\)人,第三次淘汰了\(t_3\)人,那么,第三次得到的奖金是 \(\frac{t_3}{n - t_1 - t_2}\) ——问,选手JOE能在这次答题中最多能获得多少奖金。
题解:作一个简单证明:
假设每次淘汰一个人获得的奖金比每次淘汰两个人获得的奖金多,数学式子表示如下:
\(\frac{1}{n} + \frac{1}{n - 1} > \frac{2}{n}\)
\(\frac{2n-1}{n(n-1)} > \frac{2n-2}{n(n-1)}\)
\(\frac{2n-1}{n(n-1)} > \frac{2n-1}{n(n-1)} - \frac{1}{n(n-1)}\)
因为n>0,所以以上每个分数都是正数,所以原式\(\frac{1}{n} + \frac{1}{n - 1} > \frac{2}{n}\)成立。
所以该题的答案是 \(\sum^{n}_{i=1} \frac{1}{i}\) ,最后注意输出的是12位小数。
// https://codeforces.com/contest/1293/problem/B
#include<iostream>
#include<cstdio>
using namespace std;
int n;
int main()
{
scanf("%d", &n);
double ans = 0;
for(int i = n; i > 0; i--){
ans += 1.0 / i;
}
printf("%.12f\n", ans);
return 0;
}
C
题意:有一个2 * n大小的空间,女孩如果能从从(1, 1)逃到(2, n)处即算成功逃脱,但,空间每次会改变一块(x, y)处的状态——起始时,2 * n都是安全的地,当安全地被选中时,它会变成岩浆地(不能通过此地),当岩浆地再次被选中时,它会再次变成安全地——问,女孩每次在砖块改变后,是否能逃出去(小女孩的体力与花费的时间不计入其中)。
题解:通过画图可以知道,只有上(下)相邻的砖块都变成岩浆地时,女孩才不能逃出去,即:
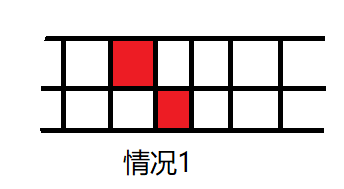
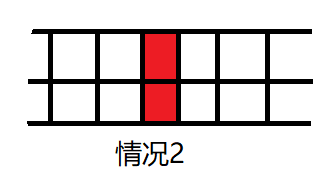
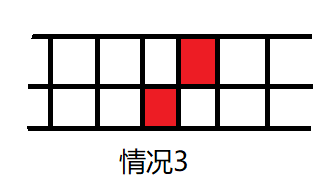
(情况4,5,6就是把情况1,2,3倒过来)
》》》而且,题目只需要判断女孩能不能逃出去,所以只需要判断空间是否有以上6种情况之一。因此,可以把情况量化,记录这种情况的次数,当次数为0时,即可逃出去。因为这里的n的范围是2 ~ 1e5,可以用bool值表示该块是否为安全地。
// https://codeforces.com/contest/1293/problem/C
#include<iostream>
#include<cstdio>
using namespace std;
int n, q, r, c;
bool maze[5][100005];
int stop;
int main()
{
scanf("%d %d", &n, &q);
while(q--){
scanf("%d %d", &r, &c);
bool flag = false; // 标记是否进行了消除
if(maze[r][c]) {
maze[r][c] = false;
flag = true;
}
else maze[r][c] = true;
if(!flag){ // 只有当有岩浆地产生时,才有可能堵住
if(r == 1){ // 区别了上下层
if(maze[2][c + 1]) stop += 2;
if(maze[2][c - 1]) stop += 2;
if(maze[2][c]) stop += 2;
}
else {
if(maze[1][c + 1]) stop += 2;
if(maze[1][c - 1]) stop += 2;
if(maze[1][c]) stop += 2;
}
}
else {
if(r == 1){
if(maze[2][c - 1]) stop -= 2;
if(maze[2][c + 1]) stop -= 2;
if(maze[2][c]) stop -= 2;
}
else {
if(maze[1][c - 1]) stop -= 2;
if(maze[1][c + 1]) stop -= 2;
if(maze[1][c]) stop -= 2;
}
}
if(stop) printf("No\n");
else printf("Yes\n");
}
return 0;
}
D
题意:偶像A在(xs, ys)处,她在坐标轴上能活动t秒,每秒她只能往上下左右方向移动一次(不能斜着走)。她的目标去去到目的地。目的地的生成条件是:第0个目的地在 \((x_0, y_0)\),第i个目的地在\((a_x · x_{i-1} + b_x,\ a_y · y_{i-1} + b_y)\) ,其中\(x_{i-1},\ y_{i-1}\) 指的是第i-1个目的地位置的(x,y)。问,偶像A最多能到多少个目的地。
题解:假如偶像A能到达其中一个目的地,那么,偶像A要走到下一个目的地的时候,肯定走的是两地的最短距离,所以可以先算出目的地两两之间的距离,然后让偶像A依次以每个能到达的第i个目的地作为起点,走去下一个目的地。因为数据很大的缘故,但即便数据很大,在1e18范围内目的地也不会很多(可以在自己跑一下),所以这题的难点其实在处理数据的溢出上——因为第i个目的地的(x,y)只会比第i-1个目的地的(x,y)要大,所以如果第i个目的地比第i-1个的(x,y)要小时,就发生了溢出;另外,如果第i个目的地的(x,y)已经达到了1e18这么大的级别时,也是不能取的,因为t的最大值只能取1e16,否则容易造成后面算总和的时候的溢出。
(这题让我见识了数据溢出的可怕性了)
// https://codeforces.com/contest/1293/problem/D
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long LL;
const LL INF = 1e18;
LL x0, y0, ax, ay, bx, by, xs, ys, t;
struct node{
LL x, y;
}pla[1003];
LL cost[1003];
LL labs(LL a, LL b){
if(a > b) return a - b;
else return b - a;
}
int main()
{
scanf("%I64d %I64d %I64d %I64d %I64d %I64d", &x0, &y0, &ax, &ay, &bx, &by);
scanf("%I64d %I64d %I64d", &xs, &ys, &t);
int cnt = 1;
pla[0].x = x0; pla[0].y = y0;
while(true){ // 生成目标点
LL nx = ax * pla[cnt - 1].x + bx;
LL ny = ay * pla[cnt - 1].y + by;
// 两个判断
if(nx > INF || ny > INF || nx < pla[cnt - 1].x || ny < pla[cnt - 1].y) break;
pla[cnt].x = nx; pla[cnt].y = ny;
cnt++;
}
// 求前序列和
cost[0] = 0;
for(int i = 1; i <= cnt; i++){
cost[i] = cost[i - 1] + labs(pla[i - 1].x, pla[i].x) + labs(pla[i - 1].y, pla[i].y);
}
LL ans = 0; LL nc, tmp;
for(int i = 0; i < cnt; i++){
nc = labs(xs, pla[i].x) + labs(ys, pla[i].y);
for(int j = cnt - 1; j >= 0; j--){
if(j >= i){ // 往下走
tmp = nc - cost[i] + cost[j];
if(tmp < 0) continue;
if(tmp <= t){
if(j - i + 1 > ans) ans = j - i + 1;
}
}
else { // 往上走
tmp = nc - cost[j] + cost[i];
if(tmp < 0) continue;
if(tmp <= t){
if(i - j + 1 > ans) ans = i - j + 1;
}
}
}
}
printf("%I64d\n", ans);
return 0;
}
写在最后:
D题思路上是没问题的,但因为比较少做这种大数据的类型,所以测试的时候看了cf的数据,算是半完成了*1800的题吧。寒假快乐。



