1 月日记

Hello 2025！

1.1

跨年夜微信上发了 \(\geq 20\) 条新年快乐，收到了来自好朋友的红包，金额不多但是心意满满，而且还有她写给我的一封信，我哭死。

早上跟朋友去了趟天府红（专门卖谷子的商场），买了几个名柯的盲袋，意外之喜，出了一个基德的限量款，吧唧新兰一起买的。

晚上返校。

晚自习写了一份学习笔记：二反 & 容斥

心有点累。

「打上花火，往事流转宛若灿烂烟火；忘却过去，唯能忆起君の名字」

1.2

Keep on 容斥 & 二反

P3349 [ZJOI2016] 小星星

学到了新东西：子集反演。

个人领悟感觉和二反有异曲同工之妙，找到博客甩在个人主页了。

其实题目翻译过来就是一个 \(n\) 个结点的无向图（无自环重边）和 \(n\) 个结点的树，对于原本的无向图每个点有编号，树上则没有，问给树上点编号使得其成为一棵原图的生成树的编号方案数。

记用集合 \(S\) 给树编号，且 \(S\) 内每个元素至少用一次的方案数为 \(f_S\)，又记 \(g_S\) 为 \(S\) 内每个元素恰好用一次的方案数（其实本来应该是至多一次，但是抽屉原理得到这里至多和恰好等效）。

最终答案为 \(f_{\{1,2,\dots,n\}}\)，考虑如何推。

每次我们钦定选择 \(S\) 的子集 \(T\)，我们可以得到：

\[g_S = \sum\limits_{T \subseteq S}{f_T} \]

根据子集反演：

\[f_S = \sum\limits_{T \subseteq S}{(-1)^{\left|{S}\right| - \left|{T}\right|}g_T} \]

看的出来与二反很类似。

现在考虑如何求 \(g_T\)，记 \(dp_{u,x,st}\) 表示结点 \(u\) 编号为 \(x\) 整树编号状态为 \(st\) 的方案数，枚举状态每次找到在状态中的结点，以下表示为 \(num_i\)，接着树形 dp，这样可以砍掉 dp 数组存状态那一维，以下转移方程：

\[dp_{u,num_i} = dp_{u,num_i} \times \sum\limits_{k=1}^{\operatorname{popcount}(st)}{dp_{v,num_k}[e_{u,v}]} \]

其中 \(v \in son_u\)，\(e_{u,v}\) 为表示在原图中是否到达的邻接矩阵，方括号为艾弗森括号。

由此得到：

\[g_T = \sum\limits_{i=1}^{\operatorname{popcount}(st)}{dp_{1,num_i}} \]

然后统计答案即可，注意 \(\left|{T}\right| = \operatorname{popcount}(st)\)。

P3158 [CQOI2011] 放棋子

考虑由一种棋子放的情况推到 \(c\) 种棋子放的情况。

记 \(dp_{i,j,k}\) 表示前 \(i\) 行 \(j\) 列恰好放完了 \(k\) 种棋子的方案数，这是总的。

记 \(f_{i,j,k}\) 表示前 \(i\) 行 \(j\) 列恰好放完 \(cnt_k\) 个 \(k\) 种棋子的方案数，注意到我们定义的是恰好，于是果断记 \(g_{i,j,k}\) 表示前 \(i\) 行 \(j\) 列至多放完 \(cnt_k\) 个 \(k\) 种棋子的方案数，这样就可以从二反入手，得到：

\[g_{i,j,k} = \sum\limits_{p=0}^{i}\sum\limits_{q=0}^{j}\binom{i}{p}\binom{j}{q}f_{p,q,k} \\ \ \\ g_{i,j,k} = \binom{i \times j}{cnt_k} \]

二反得到 \(f\)：

\[f_{i,j,k} = \sum\limits_{p=0}^{i}\sum\limits_{q=0}^{j} (-1)^{(i+j) - (p+q)}\binom{i}{p}\binom{j}{q}g_{p,q,k} \]

每次枚举一个子矩阵进行转移，初始化 \(dp_{0,0,0} = 1\)：

\[dp_{i,j,k} = \sum\limits_{p=1}^{i}\sum\limits_{q=1}^{j} \binom{i}{p}\binom{j}{q} dp_{i - p,j - q, k - 1} \times f_{i,j,cnt_k} \]

由于棋子可以每行每列任选放置，统计答案：

\[\sum\limits_{i=0}^{n}\sum\limits_{j=0}^{m}\binom{n}{i}\binom{m}{j}dp_{i,j,c} \]

P4515 [COCI2009-2010#6] XOR

两个三角形的交的顶点：

\[(\max(x_1,x_2),\max(y_1,y_2)) \]

腰长：

\[\max(x_1 + y_1 + r_1,x_2 + y_2 + r_2) - \max(x_1,x_2) - \max(y_1,y_2) \]

显然的，对于所有三角形的交，这样算定会算重，考虑容斥，由于此处容斥的集合是三角形面积，容斥系数为 \((-2)\)。

注意到 \(N \leq 10\)，考虑状压，容斥系数为 \((-2)^{\operatorname{popcount}(st) - 1}\)，答案即为：

\[\sum\limits_{i=1}^{2^n-1}{(-2)^{\operatorname{popcount}(i) - 1} S_{\cap}^{\operatorname{popcount}(i) - 1}} \]

其中 \(S_{\cap}\) 表示状态 \(i\) 三角形交的面积大小。

体育课和班上同学分队踢了 40min，发现前场只有我和另一位俩进攻，最后也是累到躺草皮上，今天没状态也是绝佳机会头球没顶到、凌空无人防守打飞（

哎我真服了我在干嘛。

没吃晚饭饿到爆炸，洗洗睡了。

可恶小保底歪莫娜了我还得攒着抽茜特菈莉，住校生尝试上半攒出 30 抽来（

1.3

上午 %你赛 \(0 + 0 + 20 + 10 = 30\)

哎不是我赛时在干嘛，赛后 T1,T2 轻松补出来，怎么会没想到呢。

T1

赛时以为又是数位 dp，发现不可做，开始想高精 + 贪心（\(a,b \leq 10^3\)）。

显然的一个结论，从大到小取数一定是最优的。

考虑如何具体操作，为了使乘积最大，我们需要将待填的数字 \(num\) 放到已填数 \(a',b'\) 更小的后面，一开始先从大到小间隔着填到 \(a',b'\) 中，默认 \(b > a\)，\(a'\) 填完后面全分给 \(b'\)。

对于第一个 \(a'_{i} > b'_{i}\)，我们不对其进行交换，这是为了保证乘积最大（保证最高位得最大），对于之后的 \(a'_i > b'_i\) 进行交换，所有操作进行完了再高精乘即可，WA 了两发都是换行打错了。

T2

\(N \leq 5 \times 10^5\)

显然的，Alice 作为先手的情况下会操作 \(\lceil{\frac{n}{2}}\rceil\) 次，由于 Alice 只能拿连续的一段区间，即她的总分为连续的一段区间和，由于 Bob 也采用最优策略，他一定有办法限制 Alice 的得分最小，即 Alice 的得分为区间长度为 \(\lceil{\frac{n}{2}}\rceil\) 的和所有最小值中的最大值，写出了全场最劣解：线段树，常数太大导致的。

破环成链，维护区间和的最小值，再询问区间取最大值。

哎我赛时怎么唐完了（太困了）。

T4

屎山分块，哎我真服了。

分块处理大环，暴力处理小环，每次 \(2\) 操作等同于给 \(1\) 操作加偏移量，代码屎山，我【数据删除】的调了好久，极度诠释了：“差之毫厘谬以千里”。

P6846 [CEOI2019] Amusement Park

看到 \(n \leq 18\) 首先想到状压。

记 \(dp_{st}\) 表示当前给无向图定向后 DAG 的状态，对于经过 \(k\) 次定向后的 DAG，只需要 \(m - k\) 次定向即可变成反图，我们恰需要 \(\frac{m}{2}\) 次，故答案为 \(dp_{2^n-1} \times \frac{m}{2}\)，现在考虑怎么推 dp。

对于当前状态 \(st\)，理解为当前的边集为 \(S\)，给 \(S\) 定向后全图为 DAG 的方案数，枚举子集 \(T\)，容易发现会有算重的情况，在枚举子集时会存在 \(T_1 \subseteq T_2\) 的情况，需要容斥，得到 dp 方程：

\[dp_{st} = \sum\limits_{i \in st}{(-1)^{\operatorname{popcount}(i) + 1} \times dp_{st \oplus j}} \]

对 OI 的热爱大不如以前了，【数据删除】，为什么还要硬着头皮学呢？ ——【数据删除】

1.4

得知寒假能放整整 17 天，开心极了（

但是年前的安排成功卡掉世界线漫展，差评。

P3160 [CQOI2012] 局部极小值

注意到 \(n \leq 4, m \leq 7\)，考虑状压。

对于无解情况，只需要判局部最小值周围是否有其他的局部最小值。

记 \(dp_{i,st}\) 表示已经确定了 \(i\) 个局部最小值，总状态为 \(st\) 的答案，dfs 遍历，每次找出满足条件的局部最小值点数 \(cnt\)，答案显然为所有状态之和，有转移：

\[dp_{i + 1,st | j} = \sum\limits_{i=1}^{cnt}{dp_{i,st}} (j \in st) \]

对于当前确定了 \(i\) 个局部最小值，若枚举状态中确定的局部最小值个数 \(s\) 比 \(i\) 大，并不会产生贡献。

对于不是局部最小值的地方，记 \(siz\) 表示可以使用的数的个数，有转移：

\[dp_{i + 1,st} = \sum\limits_{i=1}^{cnt}{dp_{i,st} \times (siz - i)} \]

最终结果 \(dp_{n \times m, 2^{cnt} - 1}\)，但是，过程中会出现 \(st_i \subseteq st_j\) 的情况，需要考虑容斥，对于 dp 所求的定义转化一下：\(f_{i}\) 表示至少包含 \(i\) 个局部最小值点的方案，\(g_i\) 表示恰好包含 \(i\) 个局部最小值点的方案，对于需要满足的点集 \(S\)：

\[g_i = \sum\limits_{i=0}^{n - \left|{S}\right|}{(-1)^i f_i} \]

dfs 遍历完所有行之后每次统计答案即可。

P1715 [USACO16DEC] Lots of Triangles P

记区域点数为 \(cnt_x\)，\(cnt_{\triangle{ABC}} = cnt_{Blue} + cnt_{Red} - cnt_{Green} + cnt_{l}\)，其中 \(cnt_l\) 指在 \(l\) 上且在三角形内的点。

其实就可以看作 \(l_{AB}\) 下方点数 \(+\) \(l_{BC}\) 下方点数 - \(l_{AC}\) 下方点数，然后实现就显然了，但是存在 \(l_{AC}\) 在 \(l_{AB},l_{BC}\) 上方的情况，判一下。

[AGC005D] ~K Perm Counting

正难则反，考虑有多少 \(\left|{p_i - i}\right| = k\) 的方案。

记 \(f_s\) 表示至少 \(s\) 个满足 \(\left|{p_i - i}\right| = k\) 的 \(i\)，\(g_s\) 表示恰好 \(s\) 个满足的 \(i\)，二反：

\[g_s = \sum\limits_{i=0}^{s}{(-1)^{i}f_i} \]

考虑求 \(f_i\)，既然要满足要求，\(p_i\) 和 \(i\) 一定满足一个二分图：

对于每一条链，只要链顶不连边，一定满足条件。

记 \(dp_{i,j,0/1}\) 表示当前第 \(i\) 个点，连了 \(j\) 条边，\(i,i-1\) 之间是否连边的方案数。

\[dp_{i,j,0} = dp_{i - 1,j,0} + dp_{i - 1,j,1} \]

如果不是链顶：

\[dp_{i,j,1} = dp_{i-1,j-1,0} \]

最后得到 \(f_i = dp_{2n,i,0} + dp_{2n,1,1}\)。

答案 \(\sum\limits_{i=0}^{n}{g_i}\)。

[AGC040C] Neither AB nor BA

对于奇数位置的字符，有且仅有可能它被偶数位的字符连带删去，翻转奇数位的 \(\texttt{A}\) 或 \(\texttt{B}\)，变成了讨论不删 \(\texttt{AA,BB}\) 合法字符串的数量，对于 \(\texttt{A,B}\) 哪一个的字符数量大于 \(\frac{n}{2}\)，其必是固定的，考虑总方案减去除去大于 \(\frac{n}{2}\) 的方案，总方案 \(3^n\) 显然。

枚举大于 \(\frac{n}{2}\) 的个数，方案数 \(\sum\limits_{i=\frac{n}{2} + 1}^{n}{2^{n-i}(n-i)!}\)，意为对于 \(i > \frac{n}{2}\)，剩余 \(n - i\) 随意排列任意选取另外两个字符的方案数，最后答案 \(3^n - \sum\limits_{i=\frac{n}{2} + 1}^{n}{2^{n-i}(n-i)!}\)。

[ARC100E] Or Plus Max

高维前缀和板。

用 pair 维护最大值和次大值，因为若 \(x \operatorname{or} y = K\)，答案就为前缀最大值，因此转化为 \(x \operatorname{or} y \subset K\)，即维护子集最大次大，高维前缀和统计一下。

1.5

平平无奇的周末。

晚上返校，来的在车上反思了很多。

反思了最近待人处事的一些不对，以及一些学习上的问题。

最近的几个月一直都一心求成，准确来说，一直以来都是这样，总是希望自己在短时间内能够提升水平，在短时间内学懂新知，在短时间内做出一道题，显然，这样的心态最终只会让结果单调不增，我之前有意识到这个问题，但是当时的我并没有放过多心思在这个问题上。

需要做出改变。

机房的大家都开始稳步提升，我仿佛还停留在过去，周围带来的压力也更大，但是俗话说得好：适当的压力可以使人进步。

调整心态是最重要的，或者说是调整学习方法，亦或者说是调整节奏。

不会做的题，自己为什么不去想然后尝试一下呢？不尝试永远不知道结果怎样。

担心的事也很多。

每天除了担心鸡毛蒜皮的小事，更多的，我感到更焦虑的是未来。

自己现在的杂鱼一样的 OI 水平，很难说能在明年拿 NOIP 一等，更别说能冲省队，但是，人们往往站在当下这个角度去描述未来，自然的，谁都想不到未来的自己会是怎么样的（预言家被刀了），上半程一路风顺，下半程说不定是狂风暴雨的洗礼，yishu2 有句话说的很好：“我不在乎你们的结果怎样，但是过程是很重要的。”努力之后的结果是什么，在当下担心毫无所谓。

从当下开始做出改变。

请不要相信，胜利就像山坡上的蒲公英一样唾手可得，但是请相信，世上总有一些美好，值得我们全力以赴，哪怕粉身碎骨。 —— 贺伟

1.6

自行补了 hello 2025 前四题。

Solution to B

Solution to D

E 听 Jmr 讲了，总之就是转成 \(0/1\) 边权二分是否小于等于 \(k\)，总之乱霍霍一通也是过了。

CF1208F Bits And Pieces

题意中的式子转化成：

\[\overline{d_i} \& d_j \& d_k \]

首先贪心的，从高到低枚举每一位，首先需要明白的是，在保证答案最大的情况下，能选更小的 \(i\) 和更大的 \(j,k\) 就一定选。

所以说我们只需要求对于当前枚举的集合的超集中是否有两个比 \(i\) 大的下标即可，高位前缀和维护最大值次大值即可。

和高中的同学们踢球已经不止一个人问我要不要加它们球队踢我们学校联赛了 （？

1.7

上午 %你赛，成功暴零喜提全场最低。

喵的我要自闭了。

T1

喵它宝贝的赛时想的 DP 成功挂掉，如果要实现能过还它宝贝的是全场最劣解。

喵它宝贝的竟然是 2-SAT。

对于 \(x,y\) 列 \(1\) 的个数：

• 如果 \(1\) 的个数和 \(> 2\)，无解。

• 如果 \(1\) 的个数和 \(< 2\)，那它宝贝的是绝对有解的。

• 如果 \(1\) 的个数和 \(= 2\)，就需要它宝贝的分讨了。

1. 如果两个 \(1\) 在同一列，则它宝贝的 \(1\) 所在的两行必须翻转一个。
2. 如果一列一个，要它宝贝的两行都翻转，要么都不。

然后就可以他宝贝的并查集维护了，对于 \(1\) 情况合并 \((x,y + n),(x + n,y)\)，对于 \(2\) 情况合并 \((x,y),(x + n, y + n)\)，然后它宝贝的再判一下 \((x,x+n)\) 是否在同一连通块，如果是就无解，最后答案就它宝贝的比较显然了：\(2^{\frac{cnt}{2}}\)，其中 \(cnt\) 为连通块个数。

T2

首先：\(a_{i + 1} - a_{i} = 1 \to a_{i + 1} - ( i + 1) = a_i - i\)，转化成使区间内所数相等。

喵它宝贝的这第一步转化赛时根本没想到，这辈子有了。

显然只需要将区间的数全部变成中位数一定是最它宝贝的优的，用两个 multiset 维护动态窗口内大于中位数和小于中位数的数，分别记它们为 s1, s2。

对于中位数的查询：

• 窗口大小为偶，中位数为 \(\frac{s1.rbegin() + s2.begin()}{2}\)。
• 否则，中位数为 \(s2.begin()\)。

对于数的插入：

• 如果 s1,s2 均为空，则插入到 s2。
• 否则判断是否 \(\geq s2.begin()\)，如果是则插入到 s2，否则插入到 s1。

为使中位数符合预期，s1,s2 的大小差应 \(\leq 1\)，需要对 s1,s2 进行一个平衡操作。

• 如果 s2 中的元素多于 s1 的个数 $ + 1$，将 \(s2.begin()\) 插入 s1。
• 否则如果 s1 元素多于 s2，，将 \(s1.rbegin()\) 插入 s2。

最后记 \(sum_a,sum_b\) 分别为 s1,s2 内的和，\(mid\) 为中位数，答案即为 \(s1.size() \times mid - sum_a + sum_b - s2.size() \times mid\)。

喵它宝贝的。

T3

Solution

喵它宝贝的。

无奖竞猜：今天日记中有多少个喵，多少个宝贝的？

21:20 下班！艹！

1.8

斜率优化，启动！

一看专题抓的题，全紫，第一反应是我做鸡毛啊。

果断先补容斥剩的两道题。

P6551 [COCI2010-2011#2] CRNI

\(O(n^6)\) 不用说。

\(O(n^4)\) 枚举两个不相交的黑色子矩阵。

考虑如何结合容斥计算（搬题解的一张图）：

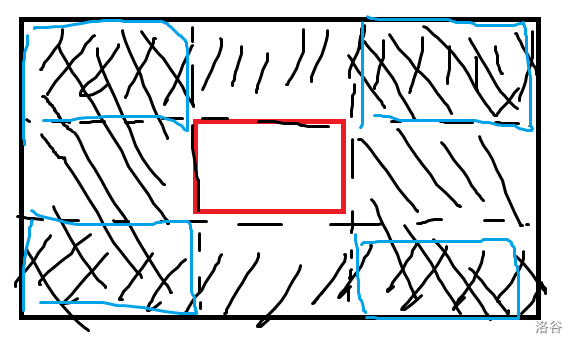
在大的黑色矩阵中剔除一个小的黑色矩阵（红框），最终的答案贡献即为上下左右的黑色矩阵的贡献减去四个角（蓝框）的贡献。

所以问题成功转化为求一个大的黑色矩阵中所有黑色子矩阵的贡献和，我们可以二位前缀和预处理然后转化成以 \((i,j)\) 为右上角的矩阵的贡献，单调栈可以维护，复杂度 \(O(n^2)\)。

瓶颈在于我们枚举矩形的 \(O(n^4)\)，首先想到预处理给优化掉，其实需要进行枚举的就是 \(2\) 种矩阵，边相接和角相接的矩阵，预处理就能将总复杂度优化成 \(O(n^2)\)。

[AGC039C] Division by Two with Something

机房大佬写的题解

Orz.

P2365 任务安排（最弱版）

P10979 任务安排 （中档）

P5785 [SDOI2012] 任务安排（最强版）

三者放一起是有原因的，个人评价三者算是斜率优化 dp 入门三件套，故写题解：click。

P3195 [HNOI2008] 玩具装箱

见 oiwiki

P2120 [ZJOI2007] 仓库建设

很有意思的一道题。

显然对于货物移动的代价为 \(p_i \times x_i\)，记 \(dp_i\) 表示在 \(i\) 建工厂使得前 \(i\) 均不被淹没的最小花费，转移柿子：

\[dp_i = \min_{j=0}^{i-1}\{dp_j + c_i + \sum\limits_{k=j+1}^{i}{(x_i - x_k) \times p_k}\} \]

令 \(s_i = \sum\limits_{k=1}^{i}{x_k \times p_k}\)，\(p\) 做前缀和并拆掉 \(\min\)（故技重施）：

\[dp_{i} = dp_{j} + c_i - s_i + s_j + x_i \times p_i - x_i \times p_j \]

不妨设 \(a,b\) 两决策点，且 \(b\) 优于 \(a\)：

\[dp_{a} + c_i - s_i + s_a + x_i \times p_i - x_i \times p_a < dp_{b} + c_i - s_i + s_b + x_i \times p_i - x_i \times p_b \\ \ \\ \Downarrow \\ \ \\ dp_{a} + s_a - x_i \times p_a <dp_{b} + s_b - x_i \times p_b \\ \ \\ \Downarrow \\ \ \\ (dp_a + s_a) - (dp_b + s_b) <x_i \times (p_a - p_b) \\ \ \\ \Downarrow \\ \ \\ \frac{(dp_a + s_a) - (dp_b + s_b)}{(p_a - p_b)} <x_i \]

故斜率优化，决策点集 \((p_i,dp_i + s_i)\)，\(p_i,s_i\) 单调递增，做法为 \(O(n)\)，只需要判 \(p_i = p_{i-1}\) 的情况，若此时 \(y > 0\) 视作正无穷，反之 \(y < 0\) 视作负无穷，\(y = 0\) 就为 \(0\)。

如果真正理解了并能够成功列出转移柿子，就可以快速的进行一个柿子的推和转化，斜率优化挺有意思哈。