洛谷P3369 【模板】普通平衡树 treap
网址:https://www.luogu.org/problem/P3369
题意:
编写一个数据结构在每次$O(logn)(1 \leq n \leq 1e6)$完成以下功能:
一、插入一个数到序列中;二、在序列中删除某一个数;三、找到第$k$大;四、询问第$k$大的数;五、找到$x$的前驱,六、找到$x$的后继。
题解:
很显然,二叉搜索树就可以完成这个任务,不过最坏情况下,二叉树会退化成链,就会超时,因此我们就需要平衡二叉树,其中较为容易编写,速度又快的是$treap$。$treap$分为有旋$treap$和无旋$treap$,前者速度快,但不支持持久化,后者速度慢,但支持持久化。
一、有旋treap
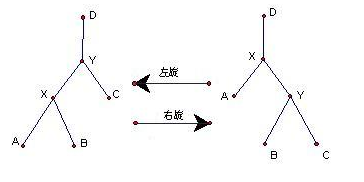
treap的节点的权值维护了二叉树的性质,为了平衡,就需要通过另外一个数维护堆性质使其平衡,这个数就是每一个节点对应的随机数。旋转的时候按照随机数进行旋转,分为左旋和右旋,如图:
(参考博客:https://blog.csdn.net/K346K346/article/details/50808879)
左旋和右旋
显然,右旋就是原树根的左子树变成树根,然后原树根的左子树的右子树变成原树根的左子树,左旋同理。易证旋转后二叉树性质不变。
插入时,先找到插入点,然后回溯时旋转。
删除较为复杂,删除时,先找到删除点,然后观察子树的随机数值选择一个子树作为删除后的树根,然后通过旋转把需要删除的节点移动到叶子后删除。
查询操作易于理解,看代码即可。
AC代码:
#include <bits/stdc++.h>
using namespace std;
const int MAXN=100005;
const int inf=0x3f3f3f3f;
struct Treap
{
struct node
{
int val, rnd, lc, rc, size, num;
};
int cnt=0;
node tr[MAXN];
void init()
{
cnt=0;
}
int _rand()
{
static int seed=12345;
return seed=(int)seed*482711LL%2147483647;
}
void pushup(int p)
{
tr[p].size=tr[tr[p].lc].size+tr[tr[p].rc].size+tr[p].num;
}
void right(int &k)
{
int tmp=tr[k].lc;
tr[k].lc=tr[tmp].rc;
tr[tmp].rc=k;
tr[tmp].size=tr[k].size;
pushup(k);
k=tmp;
}
void left(int &k)
{
int tmp=tr[k].rc;
tr[k].rc=tr[tmp].lc;
tr[tmp].lc=k;
tr[tmp].size=tr[k].size;
pushup(k);
k=tmp;
}
void insert(int &p,int x)
{
if(p==0)
{
p=++cnt;
tr[p].val=x;
tr[p].num=tr[p].size=1;
tr[p].lc=tr[p].rc=0;
tr[p].rnd=_rand();
return;
}
++tr[p].size;
if(x==tr[p].val)
++tr[p].num;
else if(x<tr[p].val)
{
insert(tr[p].lc,x);
if(tr[tr[p].lc].rnd<tr[p].rnd)
right(p);
}
else if(x>tr[p].val)
{
insert(tr[p].rc,x);
if(tr[tr[p].rc].rnd<tr[p].rnd)
left(p);
}
}
void del(int &p,int x)
{
if(p==0)
return;
if(tr[p].val==x)
{
if(tr[p].num>1)
--tr[p].num,--tr[p].size;
else
{
if(tr[p].lc==0||tr[p].rc==0)
p=tr[p].lc+tr[p].rc;
else if(tr[tr[p].lc].rnd<tr[tr[p].rc].rnd)
right(p),del(p,x);
else if(tr[tr[p].lc].rnd>tr[tr[p].rc].rnd)
left(p),del(p,x);
}
}
else if(tr[p].val<x)
--tr[p].size,del(tr[p].rc,x);
else
--tr[p].size,del(tr[p].lc,x);
}
int queryrnk(int &p,int x)
{
if(p==0)
return 0;
else if(tr[p].val==x)
return tr[tr[p].lc].size;
else if(tr[p].val<x)
return tr[tr[p].lc].size+tr[p].num+queryrnk(tr[p].rc,x);
else
return queryrnk(tr[p].lc,x);
}
int querynum(int &p,int rnk)
{
if(p==0)
return 0;
if(tr[tr[p].lc].size>=rnk)
return querynum(tr[p].lc,rnk);
rnk-=tr[tr[p].lc].size;
if(rnk<=tr[p].num)
return tr[p].val;
rnk-=tr[p].num;
return querynum(tr[p].rc,rnk);
}
int queryfront(int &p,int x)
{
if(p==0)
return -inf;
if(tr[p].val<x)
return max(tr[p].val,queryfront(tr[p].rc,x));
else if(tr[p].val>=x)
return queryfront(tr[p].lc,x);
}
int queryback(int &p,int x)
{
if(p==0)
return inf;
if(tr[p].val>x)
return min(tr[p].val,queryback(tr[p].lc,x));
else if(tr[p].val<=x)
return queryback(tr[p].rc,x);
}
};
int pos;
Treap tr;
int main()
{
int n;
scanf("%d",&n);
int m,k;
tr.init();
for(int i=0;i<n;++i)
{
scanf("%d%d",&m,&k);
if(m==1)
tr.insert(pos,k);
else if(m==2)
tr.del(pos,k);
else if(m==3)
printf("%d\n",tr.queryrnk(pos,k)+1);
else if(m==4)
printf("%d\n",tr.querynum(pos,k));
else if(m==5)
printf("%d\n",tr.queryfront(pos,k));
else if(m==6)
printf("%d\n",tr.queryback(pos,k));
}
return 0;
}
二、无旋treap
无旋$treap$的核心操作是平衡树的合并和分裂,合并时,先对权值比较,然后保证
#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
struct Treap
{
struct node
{
int lc,rc,val,rnk,size;
};
node tr[MAXN];
int cnt=0;
void init()
{
cnt=0;
}
void pushup(int p)
{
tr[p].size=tr[tr[p].lc].size+tr[tr[p].rc].size+1;
}
int _rand()
{
static int seed=int(12345);
return seed = int(seed * 482711ll % 2147483647);
}
void merge(int &rt,int a,int b)//保证a的权值小于b的权值
{
if(a==0||b==0)
{
rt=a+b;
return;
}
if(tr[a].rnk<tr[b].rnk)
rt=a,merge(tr[rt].rc,tr[a].rc,b);
else
rt=b,merge(tr[rt].lc,a,tr[b].lc);
pushup(rt);
}
void split(int rt,int &a,int &b,int val)
{
if(rt==0)
{
a=b=0;
return;
}
if(tr[rt].val<=val)
a=rt,split(tr[rt].rc,tr[a].rc,b,val);
else
b=rt,split(tr[rt].lc,a,tr[b].lc,val);
pushup(rt);
}
int newnode(int val)
{
int rt=++cnt;
tr[rt].size=1;
tr[rt].val=val;
tr[rt].lc=tr[rt].rc=0;
tr[rt].rnk=_rand();
return rt;
}
void insert(int &rt,int val)
{
int x=0,y=0,n=newnode(val);
split(rt,x,y,val);
merge(x,x,n);
merge(rt,x,y);
}
void del(int &rt,int val)
{
int x=0,y=0,z=0;
split(rt,x,y,val);
split(x,x,z,val-1);
merge(z,tr[z].lc,tr[z].rc);
merge(x,x,z);
merge(rt,x,y);
}
int querynum(int rt,int rnk)
{
while(tr[tr[rt].lc].size+1!=rnk)
{
if(tr[tr[rt].lc].size<rnk)
rnk-=tr[tr[rt].lc].size+1,rt=tr[rt].rc;
else
rt=tr[rt].lc;
}
return tr[rt].val;
}
int queryrnk(int &rt,int val)
{
int x=0,y=0;
split(rt,x,y,val-1);
int tmp=tr[x].size;
merge(rt,x,y);
return tmp;
}
int queryfront(int &rt,int val)
{
int x=0,y=0;
split(rt,x,y,val-1);
int tmp=querynum(x,tr[x].size);
merge(rt,x,y);
return tmp;
}
int queryback(int &rt,int val)
{
int x=0,y=0;
split(rt,x,y,val);
int tmp=querynum(y,1);
merge(rt,x,y);
return tmp;
}
};
Treap tr;
int p;
int main()
{
int n;
scanf("%d",&n);
int m,k;
tr.init();
/*tr.newnode(0x3f3f3f3f);
tr.cnt=1;
tr.tr[1].size=0;
p=1;*/
for(int i=0;i<n;++i)
{
scanf("%d%d",&m,&k);
if(m==1)
tr.insert(p,k);
else if(m==2)
tr.del(p,k);
else if(m==3)
printf("%d\n",tr.queryrnk(p,k)+1);
else if(m==4)
printf("%d\n",tr.querynum(p,k));
else if(m==5)
printf("%d\n",tr.queryfront(p,k));
else if(m==6)
printf("%d\n",tr.queryback(p,k));
}
return 0;
}