模拟退火摘要

OI界中有两大玄学算法，一为网络流，一为模拟退火——沃·兹基硕德

---

算法思想来源

在热力学上，退火现象指物体逐渐降温的物理现象，温度愈低，物体的能量状态会低；够低后，液体开始冷凝与结晶，在结晶状态时，系统的能量状态最低。大自然在缓慢降温（亦即，退火）时，可“找到”最低能量状态：结晶态。但是，如果过程过急过快，快速降温（亦称「淬炼」）时，会导致不是最低能态的非晶形。

那么，我们可不可以把找到最优解，与形成结晶态，这两个过程联系在一起呢？

于是，模拟退火诞生了。

模拟退火算法描述

若J(Y(i+1))>=J(Y(i))(即移动后得到更优解)，则总是接受该移动

若J(Y(i+1))<J(Y(i))(即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）

根据热力学的原理，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：P(dE) = exp( dE/(kT) )

其中k是一个常数，exp表示自然指数，dE为两个状态的能量差且dE<0。这条公式说白了就是：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于dE总是小于0（否则就不叫退火了），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。

若新状态优于当前状态则以一的概率接受新状态，否则以一定概率（这个概率写上面了）接受新状态。随着温度T的降低，P(dE)会逐渐降低。

模拟演示

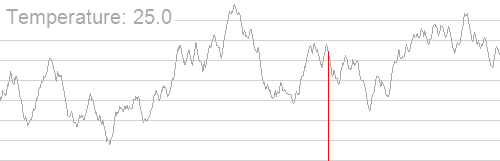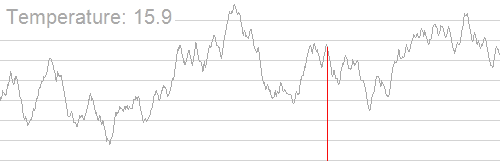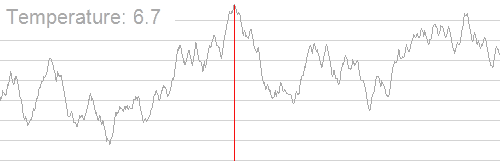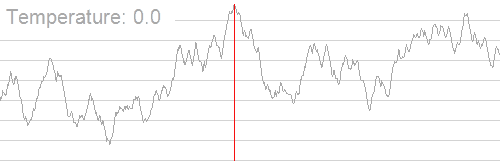
一般格式

const double jwl=...;const double Tmin=...;                    //降温率和截止温度 
double ans,...;                                                //用来存当前解 
double f(...){...}                                            //估价函数 
void mnth(){double T=...                                    //设定初始温度 
    ...                                                     //随机产生一个状态 
    ans=f(...);                                                //计算估价函数 
    while(T>=Tmin){
        ...                                                    //随机产生新的状态 
        double newans=f(...);                                //计算新状态的估价函数 
        double DE=newans-nowans;                            //新的估价函数值与全局估价函数值之差 
        if(DE<0){...ans=newans;}                            //若新状态更优则一定接受新状态 
        else if(exp(-DE/T)*RAND_MAX>rand()){...ans=newans;}    //否则以一定概率接受新状态 
            T*=jwl;                                            //降温 
        }
}

当然，实际操作的时候我们较少直接输出最终解, 而是选择在模拟退火的过程中单独维护一个解, 只在遇到更优解的时候将其更新, 增加正确率。

关于参数和调参

影响模拟退火性能的一个关键就是几个参数：

• 温度T
• 截止温度Tmin
• 降温率jwl

一般降温率jwl与1的差减少一个数量级,时间消耗大约多10倍,T和Tmin变化一个数量级, 时间消耗不会变化很大。

至于调参么，比较麻烦的是温度和降温率。首先不必顾虑，都开大一点，先把最优解跑出来。如果发现经常陷入局部最优解的话考虑增大T和jwl, 如果发现最终精度不够的话考虑减小Tmin。
然后，手动二分吧，注意每个二分的值要多跑几遍，因为模拟退火有偶然性，一次跑出最优解不代表大部分时候都能。
不过因为有两个量，还不能直接二分，应该二分套二分比较合适。

时空复杂度

时间复杂度

O(???)

空间复杂度

O(???)

例题

BZOJ3680: 吊打XXX/洛谷P1337 [JSOI2004]平衡点 / 吊打XXX

AC代码

一开始在洛谷上AC后交到BZOJ上TLE，于是在BZOJ上改AC后交到洛谷上WA。。。

最后一怒之下重调参再交，终于两个OJ都AC了。。。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;const int INF=0x7fffffff;const double jwl=0.995;const double Tmin=1e-8;
const int N=10010;int n;double x[N],y[N],w[N];double mx,my,mans;
template<class T>
inline T read(T &n){
    n=0;int t=1;double x=10;char ch;
    for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());(ch=='-')?t=-1:n=ch-'0';
    for(ch=getchar();isdigit(ch);ch=getchar()) n=n*10+ch-'0';
    if(ch=='.') for(ch=getchar();isdigit(ch);ch=getchar()) n+=(ch-'0')/x,x*=10;return (n*=t);
}double E(double nowx,double nowy){double sum=0;
    for(int i=1;i<=n;++i){double delx=nowx-x[i];double dely=nowy-y[i];
        sum+=(sqrt(delx*delx+dely*dely))*w[i];
    }return sum;
}void mnth(){double T=10000;double nowx=mx,nowy=my;double nowans=mans;
    while(T>=Tmin){double newx=nowx+(rand()%100*2-100)*T,newy=nowy+(rand()%100*2-100)*T;
        double newans=E(newx,newy);double DE=newans-nowans;
        if(DE<0){nowx=newx;nowy=newy;nowans=newans;if(nowans<mans){mx=nowx;my=nowy;mans=nowans;}}
        else if(exp(-DE/T)*RAND_MAX>rand()){nowx=newx;nowy=newy;nowans=newans;}T*=jwl;
    }
}int main(){read(n);for(int i=1;i<=n;++i){mx+=read(x[i]);my+=read(y[i]);read(w[i]);}mx/=n;my/=n;
    mans=E(mx,my);mnth();printf("%.3f %.3f",mx,my);return 0;
}