Splay算法摘要
先介绍变量定义
1 int n; 2 struct Node { //Splay节点定义 3 int fa,son[2],val,num,siz; //fa:它爸爸；son它儿子，左0右1；val：这个节点的值 4 //num：这个值的数量；siz：以它为根的子树的大小 5 void res() { //重置节点，用于删除 6 fa=son[0]=son[1]=val=num=siz=0; 7 } 8 } tree[N]; 9 int ins; 10 int root; 11 int mem[N],inm; //内存回收池（其实并没有什么用）
判断一个节点是它爸爸的左儿子还是右儿子
这个很简单，比较一下它的值和它爸爸的值就行了
1 char ison(int x) { //快速判断一个节点是它爸爸的左儿子（0）还是右儿子 （1） 2 return x==tree[tree[x].fa].son[1]; 3 }
Splay的旋转
旋转分为两种主要情况，一种是操作目标的爸爸是根，一种是操作目标的爷爷是根。
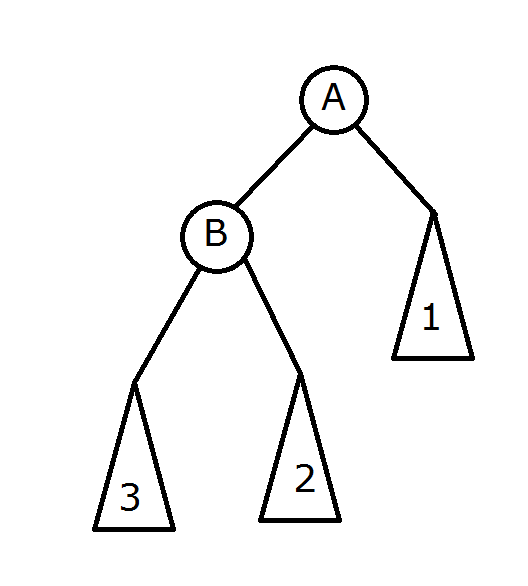如图所示，此时B为A的左儿子，要将B旋转到根。可知A,B,1,2,3的大小关系为3<B<2<A<1。所以旋转后2变成A的左子树（如图）。
同理，B为A的右儿子，则3<A<2<B<1。所以旋转后2为A的右儿子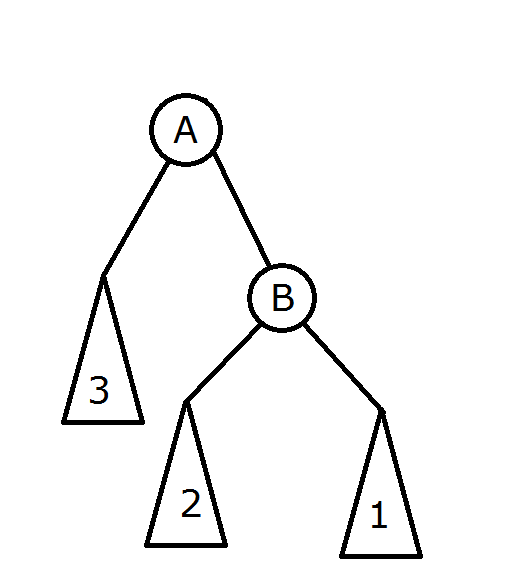
至于另外一种情况自己推一下就好啦
只是有一点，当目标它爸不是根的时候要双旋，具体为：它和它爸同为左儿子或右儿子，则先转它爸再转它；否则转它两次
事实上，这些旋转都是将一个点旋转至它的祖先位置，因此统称为上旋rotate，实现时多为单旋
OIer们耳熟能详的Splay操作其实是多次rotate，实现时一般多为双旋
1 void rotate(int x) { //上旋（即左旋和右旋） 2 int f=tree[x].fa; 3 int ff=tree[f].fa; 4 int lor=ison(x); 5 tree[ff].son[ison(f)]=x; 6 tree[x].fa=ff; 7 tree[f].son[lor]=tree[x].son[lor^1]; 8 tree[tree[x].son[lor^1]].fa=f; 9 tree[x].son[lor^1]=f; 10 tree[f].fa=x; 11 tree[f].siz=tree[f].num+tree[tree[f].son[0]].siz+tree[tree[f].son[1]].siz; 12 tree[x].siz=tree[x].num+tree[tree[x].son[0]].siz+tree[tree[x].son[1]].siz; 13 } 14 void splay(int x,int goal) { //Splay操作,将节点xSplay至节点goal的儿子（若goal为0则Splay至根） 15 while(tree[x].fa!=goal) { 16 int f=tree[x].fa,ff=tree[f].fa; 17 if(!f||!ff)break; 18 if(ff!=goal) ison(f)^ison(x)?rotate(x):rotate(f); 19 rotate(x); 20 } 21 if(!goal&&tree[x].fa&&!tree[tree[x].fa].fa)rotate(x); 22 if(goal==0)root=x; 23 }
插入
和其他平衡树一样插入就行了，就是最后的时候将其Splay到根
1 void insert(int x) { //插入一个节点并Splay到根 2 int u=root,f=0; 3 for(; u&&tree[u].val!=x; tree[u].siz++,f=u,u=tree[u].son[x>tree[u].val]); 4 if(u) tree[u].num++,tree[u].siz++; 5 else { 6 if(inm)u=mem[inm--]; 7 else u=++ins; 8 if(f)tree[f].son[x>tree[f].val]=u; 9 tree[u].fa=f; 10 tree[u].val=x; 11 tree[u].num=tree[u].siz=1; 12 } 13 splay(u,0); 14 }
查找一个数的排名
和其他平衡树一样查找，并将其Splay至根。输出时输出它的左子树的大小+1
1 void find(int x) { //查询一个数并Splay到根 2 int u=root; 3 if(!u)return; 4 for(; tree[u].son[x>tree[u].val]&&x!=tree[u].val; u=tree[u].son[x>tree[u].val]); 5 splay(u,0); 6 }
查找排名为x的数
和其他平衡树一样查找，并将其Splay至根
void finran(int x) { //查询排名为x的数并Splay到根 int u=root; if(!u)return; for(char t; tree[u].son[tree[tree[u].son[0]].siz+tree[u].num<x?1:0]&&(tree[tree[u].son[0]].siz>=x||tree[tree[u].son[0]].siz+tree[u].num<x); t=tree[tree[u].son[0]].siz+tree[u].num<x,x-=t*(tree[tree[u].son[0]].siz+tree[u].num),u=tree[u].son[t]); splay(u,0); }
查找一个数的前驱（后继）
这个简单，先找到这个数并将其Splay至根，然后沿它的左儿子（前驱）/右儿子（后继）不断找右儿子（前驱）/左儿子（后继）直至没有儿子
1 int nex(int x,int op) { //查询一个数的前驱（0）或后继（1） 2 find(x); 3 int u=root; 4 if(tree[u].val>x&&op||tree[u].val<x&&!op||!tree[u].son[op])return u; 5 u=tree[u].son[op]; 6 while(tree[u].son[op^1])u=tree[u].son[op^1]; 7 return u; 8 }
删除一个数x
首先找到x的前驱和后继，并将前驱Splay至根，后继Splay至前驱的右儿子。由于x的前驱<x<x的后继，易证此时x为后继的左儿子且以它为根的子树大小就是x的个数，直接将其数量减一（x的数量不是1）或将其重置放入内存回收池并将后继的左儿子设为0（x只有1个）。
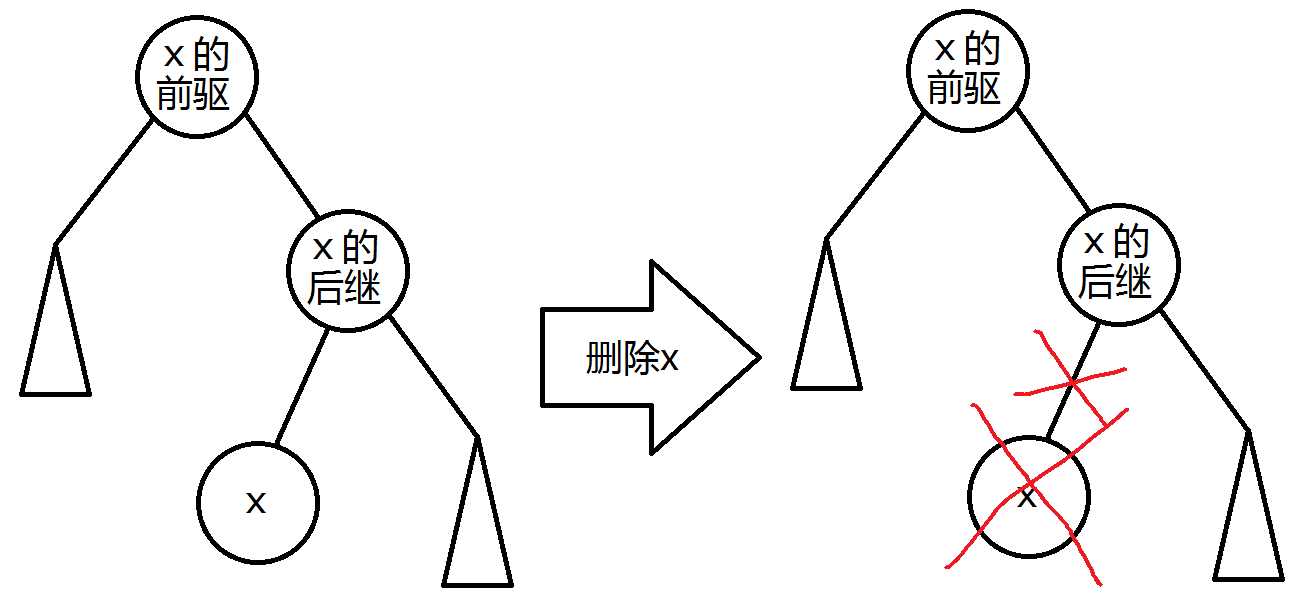
1 inline void delet(int x) { //删除一个节点 2 int la=nex(x,0); 3 int ne=nex(x,1); 4 splay(la,0); 5 if(tree[la].val==x) { 6 if(tree[la].num>1) { 7 --tree[la].num; 8 --tree[la].siz; 9 return; 10 } 11 root=tree[la].son[1]; 12 tree[root].fa=0; 13 mem[++inm]=la; 14 tree[la].res(); 15 return; 16 } 17 if(tree[ne].val==x) { 18 splay(ne,0); 19 if(tree[ne].num>1) { 20 --tree[ne].num; 21 --tree[ne].siz; 22 return; 23 } 24 root=tree[ne].son[0]; 25 tree[root].fa=0; 26 mem[++inm]=ne; 27 tree[ne].res(); 28 return; 29 } 30 splay(ne,la); 31 --tree[la].siz; 32 --tree[ne].siz; 33 int del=tree[ne].son[0]; 34 if(tree[del].num>1) { 35 tree[del].num--; 36 --tree[del].siz; 37 splay(del,0); 38 } else { 39 mem[++inm]=tree[ne].son[0]; 40 tree[del].res(); 41 tree[ne].son[0]=0; 42 } 43 }
时空复杂度
时间复杂度
splay：由于树高为均摊logn，因此复杂度为均摊O(logn)
插入、删除、查询：基于splay，因此均摊O(logn)
但常数巨大！！！
常数巨大！！！
常数巨大！！！
空间复杂度
O(n)
例题
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define INF 0x7fffffff 4 #define ME 0x7f 5 #define FO(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout) 6 #define fui(i,a,b,c) for(int i=(a);i<=(b);i+=(c)) 7 #define fdi(i,a,b,c) for(int i=(a);i>=(b);i-=(c)) 8 #define fel(i,a) for(register int i=h[a];i;i=ne[i]) 9 #define ll long long 10 #define MEM(a,b) memset(a,b,sizeof(a)) 11 const int N=100010; 12 int n;struct Node{int fa,son[2],val,num,siz;void res(){fa=son[0]=son[1]=val=num=siz=0;}}tree[N];int ins;int root;int mem[N],inm; 13 template<class T> 14 inline T read(T &n){ 15 n=0;int t=1;double x=10;char ch; 16 for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());(ch=='-')?t=-1:n=ch-'0'; 17 for(ch=getchar();isdigit(ch);ch=getchar()) n=n*10+ch-'0'; 18 if(ch=='.') for(ch=getchar();isdigit(ch);ch=getchar()) n+=(ch-'0')/x,x*=10; 19 return (n*=t); 20 }char ison(int x){return x==tree[tree[x].fa].son[1];} 21 void rotate(int x){ 22 int f=tree[x].fa;int ff=tree[f].fa;int lor=ison(x);tree[ff].son[ison(f)]=x;tree[x].fa=ff;tree[f].son[lor]=tree[x].son[lor^1];tree[tree[x].son[lor^1]].fa=f;tree[x].son[lor^1]=f; 23 tree[f].fa=x;tree[f].siz=tree[f].num+tree[tree[f].son[0]].siz+tree[tree[f].son[1]].siz;tree[x].siz=tree[x].num+tree[tree[x].son[0]].siz+tree[tree[x].son[1]].siz; 24 }void splay(int x,int goal){while(tree[x].fa!=goal){int f=tree[x].fa,ff=tree[f].fa;if(!f||!ff)break;if(ff!=goal) ison(f)^ison(x)?rotate(x):rotate(f);rotate(x);} 25 if(!goal&&tree[x].fa&&!tree[tree[x].fa].fa)rotate(x);if(goal==0)root=x;} 26 void find(int x){int u=root;if(!u)return;for(;tree[u].son[x>tree[u].val]&&x!=tree[u].val;u=tree[u].son[x>tree[u].val]);splay(u,0);} 27 void finran(int x){int u=root;if(!u)return;for(char t;tree[u].son[tree[tree[u].son[0]].siz+tree[u].num<x?1:0]&&(tree[tree[u].son[0]].siz>=x||tree[tree[u].son[0]].siz+tree[u].num<x); 28 t=tree[tree[u].son[0]].siz+tree[u].num<x,x-=t*(tree[tree[u].son[0]].siz+tree[u].num),u=tree[u].son[t]);splay(u,0); 29 }void insert(int x){ 30 int u=root,f=0;for(;u&&tree[u].val!=x;tree[u].siz++,f=u,u=tree[u].son[x>tree[u].val]);if(u) tree[u].num++,tree[u].siz++; 31 else{if(inm)u=mem[inm--];else u=++ins;if(f)tree[f].son[x>tree[f].val]=u;tree[u].fa=f;tree[u].val=x;tree[u].num=tree[u].siz=1;}splay(u,0); 32 }int nex(int x,int op){find(x);int u=root;if(tree[u].val>x&&op||tree[u].val<x&&!op||!tree[u].son[op])return u;u=tree[u].son[op];while(tree[u].son[op^1])u=tree[u].son[op^1];return u;} 33 inline void delet(int x){ 34 int la=nex(x,0);int ne=nex(x,1);splay(la,0);if(tree[la].val==x){if(tree[la].num>1){--tree[la].num;--tree[la].siz;return;}root=tree[la].son[1];tree[root].fa=0;mem[++inm]=la;tree[la].res(); 35 return;}if(tree[ne].val==x){splay(ne,0);if(tree[ne].num>1){--tree[ne].num;--tree[ne].siz;return;}root=tree[ne].son[0];tree[root].fa=0;mem[++inm]=ne;tree[ne].res();return;}splay(ne,la); 36 --tree[la].siz;--tree[ne].siz;int del=tree[ne].son[0];if(tree[del].num>1){tree[del].num--;--tree[del].siz;splay(del,0);}else{mem[++inm]=tree[ne].son[0];tree[del].res();tree[ne].son[0]=0;} 37 } 38 int main(){ 39 read(n); 40 fui(i,1,n,1){ 41 int opt,x;read(opt);read(x); 42 switch(opt){ 43 case 1:{insert(x);break;}case 2:{delet(x);break;}case 3:{find(x);cout<<tree[tree[root].son[0]].siz+1<<endl;break;} 44 case 4:{finran(x);cout<<tree[root].val<<endl;break;}case 5:{cout<<tree[nex(x,0)].val<<endl;break;}case 6:{cout<<tree[nex(x,1)].val<<endl;} 45 } 46 }return 0; 47 }
补充:区间操作
将每个节点的权值改为下标，另建变量存原权值
大概就是这些了
哦对了，现实中好像除了LCT就很少用到Splay了
PS:不要信所谓单旋spaly的邪，那只是某大神为了嘲讽人编出来的！！！
