题解：「AHOI / HNOI2017」影魔

毒瘤了一个下午。

首先这个题是裂开的，就算一个 \(p_1\) 和 \(p_2\) 的系数就好了。

先转化一下题意，设区间 \((i, j)\) 中的最大值为 \(M_{i, j}\) 。

那么 \(p_1\) 的系数就是满足 \(M_{i, j} \le \min\{k_i, k_j\}\) 的 \((i, j)\) 点对的个数，\(p_2\) 的系数就是满足 \(\min\{k_i, k_j\} < M_{i, j} < \max\{k_i, k_j\}\) 的点对个数。

然后这个第一个子任务是没有意义的，然后考虑一个 \(\mathcal O(n\times m)\) 的算法。

枚举右端点求出左端点的个数，由于你做过数区间而且有关最大最小值的题，你掏出来一个单调栈 \(stk\) 。

然后罚坐了半个小时， 你有一些惊世骇俗的发现（先很自然地把原来的序列转化为一堆形如 \((i, k_i)\) 的点）：

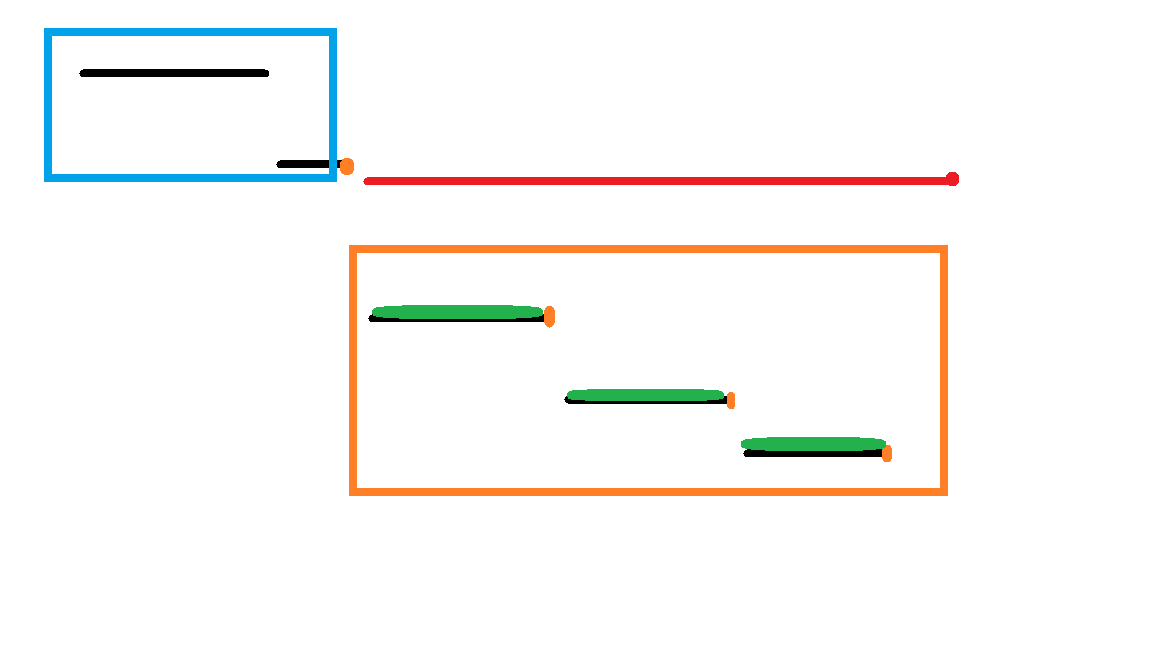
右边的这个红点是新加入的，橙色的框住的是将要被删去的单调栈的节点。

这些节点（线段）的最右端点就是最大值。

那么能和这个新节点形成 \(p_1\) 系数的节点就是图上标出的橙色节点，能成为 \(p_2\) 系数的就是这些绿色的部分以及蓝框内单调栈节点的最右端点。

最激动人心的是由于单调栈删去和加入节点的复杂度，使得这样的计算只是 \(\mathcal O (n)\) 级别的。

然后就能获得和暴力分一样的好成绩。

但是到了这个程度，就有想法了，你可以将所有这些花花绿绿的点对应到线段树下标上，然后枚举右端点，如果是 \(p_i\) 的系数就赋上 \(p_i\) 。

那么先把所有在单调栈里面的节点赋上 \(p_2\)，总体的复杂度就是一个 \(\log\) 的。

但是现在求的不是对于每个右端点的权值总和，而是一个区间，所以一个主席树就解决了。

但是由于你前几个礼拜做了一些很迷惑的操作，你考虑直接在线段树上维护历史版本和，然后也做完了。

#include <bits/stdc++.h>
#define forn(i,s,t) for(int i = (s); i <= (t); ++i)
#define form(i,s,t) for(int i = (s); i >= (t); --i)
#define rep(i,s,t) for(int i = (s); i < (t); ++i)
using namespace std;
typedef long long i64;
const int N = 2e5 + 5;
int n, m, p[N]; i64 p1, p2;
namespace SUB1 {
	int stk[N], top;
	inline void solver(int l, int r) {
		top = 0; i64 ans1 = 0, ans2 = 0;
		stk[0] = l - 1;
		forn (i, l, r) {
			while (top && p[stk[top]] < p[i]) 
				ans1 ++ , ans2 += stk[top] - stk[top - 1] - 1, top -- ;
			ans1 += (top != 0), ans2 += max(top - 1, 0), stk[++top] = i;
		}
		cout << ans1 * p1 + ans2 * p2 << '\n';
	}
	inline void solve() {
		while (m--) {
			int l, r;
			cin >> l >> r;
			solver(l, r);
		}
	}
}
namespace SUB2 {
	int rt;
	struct SGT {
		i64 sum[N << 1], val[N << 1], tags[N << 1], tagt[N << 1], tmp[N << 1], len[N << 1];
		int L[N << 1], R[N << 1], sl;
		inline void up(int p) {
			sum[p] = sum[L[p]] + sum[R[p]];
			val[p] = val[L[p]] + val[R[p]];
		}
		inline void opts(int p, i64 k) {
			val[p] += len[p] * k, tags[p] += k;
		}
		inline void optt(int p, i64 k, i64 t) {
			sum[p] += k * val[p] + t * len[p], tagt[p] += k, tmp[p] += k * tags[p] + t;
		}
		inline void down(int p) {
			if (tagt[p]) optt(L[p], tagt[p], tmp[p]), optt(R[p], tagt[p], tmp[p]);
			if (tags[p]) opts(L[p], tags[p]), opts(R[p], tags[p]);
			tmp[p] = tags[p] = tagt[p] = 0;
		}
		void Bld(int& p, int l, int r) {
			p = ++sl; len[p] = r - l + 1;
			if (l == r) return ;
			int mid = l+r >> 1;
			Bld(L[p], l, mid), Bld(R[p], mid + 1, r);
			up(p);
		}
		void upds(int p, int l, int r, int nl, int nr, i64 k) {
			assert(nl <= l && r <= nr && nl <= nr);
			if (l == nl && nr == r) return opts(p, k);
			int mid = nl+nr >> 1;
			down(p);
			if (r <= mid) upds(L[p], l, r, nl, mid, k);
			else if (l > mid) upds(R[p], l, r, mid + 1, nr, k);
			else upds(L[p], l, mid, nl, mid, k), upds(R[p], mid + 1, r, mid + 1, nr, k);
			up(p);
		}
		i64 qry(int p, int l, int r, int nl, int nr) {
			assert(nl <= l && r <= nr && nl <= nr);
			if (nl == l && r == nr) return sum[p];
			int mid = nl+nr >> 1;
			down(p);
			if (r <= mid) return qry(L[p], l, r, nl, mid);
			else if (l > mid) return qry(R[p], l, r, mid + 1, nr);
			else return qry(L[p], l, mid, nl, mid) + qry(R[p], mid + 1, r, mid + 1, nr);
		}
	} ZT;
	struct Seg {
		int id, l, r;
		Seg() {}
		Seg(int _d, int _l, int _r) : id(_d), l(_l), r(_r) {}
		inline void Rdn(int i) { id = i; cin >> l >> r; }
		inline friend bool operator < (const Seg& A, const Seg& B) {
			return (A.r == B.r) ? (A.l < B.l) : (A.r < B.r);
		}
	} S[N];
	int stk[N], top; basic_string<int> O; i64 ans[N];
	inline void solve() {
		forn (i, 1, m) S[i].Rdn(i);
		sort (S + 1, S + m + 1);
		int now = 1; ZT.Bld(rt, 1, n);
		forn (r, 1, n) {
			O.clear(), O += 0;
			while (top && p[stk[top]] < p[r]) O += stk[top], top -- ;
			O[0] = stk[top];
			reverse(O.begin() + 1, O.end());
			if (O[0]) ZT.upds(rt, O[0], O[0], 1, n, p1 - p2);
			rep (i, 1, O.size()) {
				ZT.upds(rt, O[i], O[i], 1, n, p1 - p2);
				if (O[i - 1] + 1 <= O[i] - 1) ZT.upds(rt, O[i - 1] + 1, O[i] - 1, 1, n, p2);
			}
			ZT.optt(rt, 1, 0);
			if (O[0]) ZT.upds(rt, O[0], O[0], 1, n, p2 - p1);
			rep (i, 1, O.size()) {
				ZT.upds(rt, O[i], O[i], 1, n, - p1);
				if (O[i - 1] + 1 <= O[i] - 1) ZT.upds(rt, O[i - 1] + 1, O[i] - 1, 1, n, -p2);
			}
			stk[++top] = r; ZT.upds(rt, r, r, 1, n, p2);
			while (now <= m && S[now].r == r) ans[S[now].id] = ZT.qry(rt, S[now].l, S[now].r, 1, n), now ++ ;
		}
		forn (i, 1, m) cout << ans[i] << '\n';
	}
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n >> m >> p1 >> p2;
	forn (i, 1, n) cin >> p[i];
	if (max(n, m) <= 500) SUB1 :: solve();
	else SUB2 :: solve();
	return 0;
}