「POI2019 R1」Przedszkole

Sub1 :: \(m\le 24\)

由于图上的边就是一条条限制，所以尝试容斥。

暴力枚举，先选定任意条边，钦定这些边的两端点是同一种颜色，其他点的颜色任意，设这些边相关的总点数为 \(r\) ，那么方案数为 \((n - r) ^ k\) ，容斥系数就是 \((-1) ^ {[选定边数是奇数]}\) ，可以用并查集维护。

但是有多次询问，所以直接暴力是不行的。

发现 \((n - r) ^ k\) 的个数只有 \(n\) 个，所以先算出所有 \((n - r) ^ k\) 的容斥系数就可以了。

时间复杂度 \(\mathcal O (m\times 2 ^ m + zm\log n)\) 。

Sub2 :: \(n\le 15\)

\(n\) 很小，考虑状压 DP ，传统的一个一个加点的 DP 在这里有一个很大的问题，就是无法知道所有点到底是什么颜色的。

然后考虑一个可以不用知道原来颜色的状态，所以考虑一个每次填入一块相同颜色的 DP 。

然后又由于 \(n\) 很小，所以一共只需要填上 \(n\) 次，最后方案数乘上一个组合数即可，这样又和 \(k\) 无关了。

设 \(f(i, S)\) 表示已经填入了前 \(i\) 种颜色，填上这些颜色的点的所有点的点集为 \(S\) ，保证每种颜色都存在的方案数。

那么转移为：

\[f(i, S) \leftarrow \sum_{T\subset S} f(i - 1, S \oplus T) \times [T 是独立集] \]

点集是否为独立集可以 \(\mathcal O (n2^n)\) 处理。

时间复杂度 \(\mathcal O (n3^n + zn^2)\) 。

Sub3 :: 图由多个环构成

观察下图：

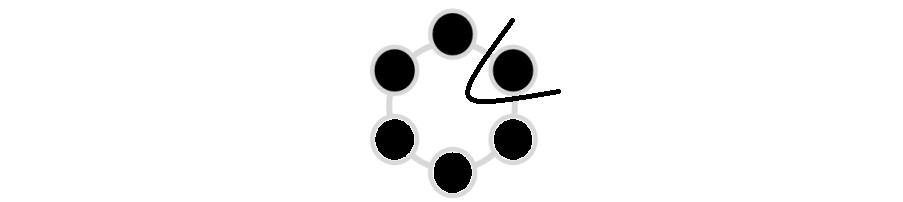
对于被划到外面的这个点的颜色方案数要么是 \(k - 1\) 要么是 \(k - 2\) 。

取决于相邻两边的点是否同色。

考虑同色的情况，把这两个点合起来变成一个点，那么就是一个长为 \(n - 2\) 的合法环。

对于异色的情况，直接把两个点接上，那么就是一个长为 \(n - 1\) 的合法环。

那么设长为 \(n\) 的合法环的方案数为 \(f(n)\) ，那么有递推式：

\[f(n) = (k - 2) \times f(n - 1) + (k - 1) \times f(n - 2) \]

可以直接矩阵乘法，但是环的个数一共为 \(n\) 。

可以发现这里有一个自然根号，对于大于 \(\sqrt n\) 的环，最多只有 \(\sqrt n\) 个，所以所有不同的环的总个数是 \(\mathcal O (\sqrt n)\) 级别的。

所以就做完了，时间复杂度 \(\mathcal O (n + m + z\sqrt n\log n)\) 。

const int Mod = 1e9 + 7;
namespace Modint {
	struct Mint {
		int res;
		Mint() {}
		Mint(int _r) : res(_r) {}
		inline friend Mint operator + (const Mint& A, const Mint& B) {
			return Mint((A.res + B.res >= Mod) ? (A.res + B.res - Mod) : (A.res + B.res));
		}
		inline friend Mint operator - (const Mint& A, const Mint& B) {return A + Mint(Mod - B.res); }
		inline friend Mint operator * (const Mint& A, const Mint& B) {return Mint(1ll * A.res * B.res % Mod); }
		inline friend Mint& operator += (Mint& A, const Mint& B) {return A = A + B; }
		inline friend Mint& operator -= (Mint& A, const Mint& B) {return A = A - B; }
		inline friend Mint& operator *= (Mint& A, const Mint& B) {return A = A * B; }
		inline friend Mint q_pow(Mint p, int k = Mod - 2) {
			Mint res(1);
			for (; k; k >>= 1, p *= p) (k & 1) && (res *= p, 0);
			return res;
		}
	} ;
}
using Modint :: Mint;
typedef long long i64;
typedef double f64;
typedef unsigned long long u64;
typedef pair<i64, i64> pii;
typedef pair<int, u64> piu;
const int N = 1e5 + 5;
const i64 INF = 1e18;
inline void init() {}
int n, m, z;
namespace SUB1 {
	const int M = 30;
	Mint cof[N]; int fa[N], u[M], v[M], lim;
	int fnd(int u) {
		return fa[u] == u ? u : fnd(fa[u]);
	}
	void dfs(int dep, int rem, int num) {
		if (dep == m) {
			if (num & 1) cof[rem] -= Mint(1);
			else cof[rem] += Mint(1);
			lim = min(lim, rem);
			return ;
		}
		dfs(dep + 1, rem, num);
		int Tu = fnd(u[dep]), Tv = fnd(v[dep]);
		fa[Tv] = Tu;
		if (Tu != Tv) dfs(dep + 1, rem - 1, num + 1);
		else dfs(dep + 1, rem, num + 1);
		fa[Tv] = Tv;
	}
	inline void solve() {
		rep (i, 0, m) Rdn(u[i], v[i]); lim = n;
		forn (i, 1, n) fa[i] = i;
		dfs(0, n, 0);
		while (z--) {
			int k; Rdn(k);
			Mint res(0);
			forn (i, lim, n) res += cof[i] * q_pow(Mint(k), i);
			Wtn(res.res, '\n');
		}
	}
}
namespace SUB2 {
	const int M = 20;
	Mint f[16][1 << 15];
	int e[16]; bool g[1 << 15]; 
	inline Mint C(int k, int r) {
		if (k < 0 || r < 0 || k - r < 0) return Mint(0);
		Mint res(1);
		forn (i, 2, r) res *= q_pow(Mint(i));
		forn (i, k - r + 1, k) res *= Mint(i);
		return res;
	}
	inline void solve() {
		forn (i, 1, m) {
			int u, v;
			Rdn(u, v); --u, --v;
			e[u] |= 1 << v;
			e[v] |= 1 << u;
		}
		rep (S, 0, 1 << n) {
			g[S] = 1;
			rep (i, 0, n) if (S >> i & 1) if (S & e[i]) {g[S] = 0; break ;}
		}
		f[0][0] = Mint(1);
		forn (i, 1, n) rep (S, 0, 1 << n) for (int T = S; T; T = S & (T - 1))
			if (g[T]) f[i][S] += f[i - 1][S ^ T];
		while (z--) {
			int k; Rdn(k);
			Mint res(0);
			forn (i, 1, n) res += C(k, i) * f[i][(1 << n) - 1];
			Wtn(res.res, '\n');
		} 
	}
}
namespace SUB3 {
	struct Mat {
		Mint a[2][2];
		Mat() {}
		Mat(Mint _a11, Mint _a12, Mint _a21, Mint _a22)  {
			a[0][0] = (_a11), a[0][1] = (_a12), a[1][0] = (_a21), a[1][1] = (_a22);
		}
		inline void init(bool I) {
			memset(a, 0, sizeof a);
			if (I) a[0][0] = a[1][1] = Mint(1);
		}
		inline friend Mat operator * (const Mat& A, const Mat& B) {
			return Mat(
				A.a[0][0] * B.a[0][0] + A.a[0][1] * B.a[1][0],
				A.a[0][0] * B.a[0][1] + A.a[0][1] * B.a[1][1],
				A.a[1][0] * B.a[0][0] + A.a[1][1] * B.a[1][0],
				A.a[1][0] * B.a[0][1] + A.a[1][1] * B.a[1][1]
			) ;
		}
	};
	bool vis[N]; vector<int> T[N];
	int dfs(int u, int lst) {
		if (vis[u]) return 0; vis[u] = 1;
		if (T[u][0] != lst) return dfs(T[u][0], u) + 1;
		else return dfs(T[u][1], u) + 1;
	}
	int siz[N], tot, rft[N], ton[N];
	inline void solve() {
		forn (i, 1, m) {
			int u, v; Rdn(u, v);
			T[u].push_back(v), T[v].push_back(u);
		}
		forn (i, 1, n) if (!vis[i]) siz[++tot] = dfs(i, i), rft[tot] = siz[tot];
		sort (rft + 1, rft + tot + 1);
		int Rn = unique(rft + 1, rft + tot + 1) - rft - 1;
		forn (i, 1, tot) siz[i] = lower_bound(rft + 1, rft + Rn + 1, siz[i]) - rft, ton[siz[i]] ++ ;
		while (z--) {
			int k; Rdn(k); Mint res(1);
			if (k <= 2) {Wtn("0\n"); continue ; }
			k %= Mod;
			Mat unit = Mat(Mint(k - 2), Mint(1), Mint(k - 1), Mint(0));
			forn (i, 1, Rn) {
				Mat trans(Mint(1), Mint(0), Mint(0), Mint(1)), lft = unit, F(Mint(k) * Mint(k - 1) * Mint(k - 2), Mint(k) * Mint(k - 1), Mint(0), Mint(0));
				for (int o = rft[i] - 3; o; o >>= 1, lft = lft * lft) (o & 1) && (trans = trans * lft, 0) ;
				F = F * trans;
				res *= q_pow(F.a[0][0], ton[i]);
			}
			Wtn(res.res, '\n');
		}
	}
}```