JOISC 2014
D1T1 - Bus
首先从后往前考虑,发现每次询问的答案只和最后乘坐的车子有关,那么答案就是到达时间 \(\le L_i\) 且终点站为 \(n\) 的车中,需要最晚出发的车。
所以设 \(f_i\) 表示需要乘坐第 \(i\) 个车的最晚出发时间,设 \(d_i\) 表示到达第 \(i\) 个点需要的最晚出发时间。
那么对于每一个车,之前必须将出发时间小于它的车的转移处理掉,所以将车子对于 \(X_i\) 排序。
对于每个车站,转移为: \(d_{b_i} \leftarrow f_i\) 。
对于每个车子,转移为: \(f_{i} \leftarrow \min\{X_i, d_{a_i}\}\) 。
对于每个询问,先存下所有终点为 \(N\) 的车子,按照 \(Y_i\) 排序,离线处理一下即可。
时间复杂度 \(\mathcal O ((N + M + Q)\log M)\) 。
struct node {
int u; i64 val;
node() {}
node(int _s, i64 _v) : u(_s), val(_v) {}
inline friend bool operator < (const node& A, const node& B) {
return A.val == B.val ? A.u < B.u : A.val < B.val;
}
} ;
int n, m, Q, a[M], b[M], id[M]; i64 dis[N], f[M], x[M], y[M], L[N], ans[N];
multiset<node> s, Fin; vector<int> F;
inline void solve() {
Rdn(n, m);
forn (i, 1, m) Rdn(a[i], b[i], x[i], y[i]), id[i] = i, f[i] = -1;
sort (id + 1, id + m + 1, [&](const int& A, const int& B) {return x[A] < x[B]; });
forn (i, 1, n) dis[i] = -1;
dis[1] = INF;
forn (i, 1, m) {
while (!s.empty() && s.begin()->val <= x[id[i]])
dis[b[s.begin()->u]] = max(dis[b[s.begin()->u]], f[s.begin()->u]), s.erase(s.begin());
f[id[i]] = min(x[id[i]], dis[a[id[i]]]), s.insert(node(id[i], y[id[i]]));
if (b[id[i]] == n) Fin.insert(node(id[i], f[id[i]])), F.push_back(id[i]);
}
Rdn(Q);
forn (i, 1, Q) Rdn(L[i]), id[i] = i;
sort (id + 1, id + Q + 1, [&](const int& A, const int& B) {return L[A] > L[B]; });
sort (F.begin(), F.end(), [&](const int& A, const int& B) {return y[A] > y[B]; });
int now = 0;
forn (i, 1, Q) {
while (!Fin.empty() && y[F[now]] > L[id[i]]) Fin.erase(Fin.find(node(F[now], f[F[now]]))), ++now;
if (Fin.empty()) ans[id[i]] = -1;
else ans[id[i]] = Fin.rbegin()->val;
}
forn (i, 1, Q) Wtn(ans[i], "\n");
}
D1T2 - Growing Vegetables is Fun
若将每个元素看成 \((i, a_i)\) ,条件等价于构造一个单峰序列。
考虑构造这个序列的过程。
对于所有值从大到小排序,首先最大值一定在中间,然后将较小值分别从中间向两边构造。
若原来一个元素的位置在 \(a_i\),最后在 \(b_i\),那么看做整个序列对于 \(b\) 作为关键字排序,那么原来题目中的操作,等价于求对于关键字 \(b\) 的逆序对个数。
发现上述构造过程有着非常好的子结构性质,所以每次只需要贪心的选择将每个元素放在左边或右边即可。
求逆序对个数可以用 BIT 快速维护,时间复杂度 \(\mathcal O (n\log n)\) 。
struct BIT {
int val[N], R, A;
inline void upd(int p) { while (p <= R) val[p] ++ , p += p & -p; }
inline int qry(int p) { A = 0; while (p) A += val[p], p -= p & -p; return A; }
} ZT;
int n, a[N], id[N]; i64 res;
inline void solve() {
Rdn(n), ZT.R = n;
forn (i, 1, n) Rdn(a[i]), id[i] = i;
sort (id + 1, id + n + 1, [&] (const int& A, const int& B) {return a[A] == a[B] ? A < B : a[A] > a[B]; });
forn (l, 1, n) {
int r = l;
while (r < n && a[id[r + 1]] == a[id[l]]) ++r;
forn (s, l, r) res += min(ZT.qry(id[s]), l - 1 - ZT.qry(id[s]));
forn (s, l, r) ZT.upd(id[s]); l = r;
}
Wtn(res, '\n');
}
D1T4 - Ramen
初赛题
将原来 \(n\) 个数字两两比较,交互次数 \(\lfloor\frac{n}{2}\rfloor\) ,将原数组分成较大的和较小的。
再在分别两个数组中找到最大值和最小值,交互次数 \(2\times \lfloor\frac{n}{2}\rfloor\) 。
然后就做完了。
#include <bits/stdc++.h>
#include "ramen.h"
using namespace std;
const int N = 1e3 + 3;
int L[N], R[N], numl, numr;
void Ramen(int N) {
for (int i = 1; i < N; i += 2) {
if (Compare(i - 1, i) == 1) {
L[++numl] = i - 1;
R[++numr] = i;
} else {
L[++numl] = i;
R[++numr] = i - 1;
}
}
if (N & 1) L[++numl] = N - 1, R[++numr] = N - 1;
int X = L[1], Y = R[1];
for (int i = 2; i <= numl; ++i) if (Compare(L[i], X) == 1) X = L[i];
for (int i = 2; i <= numr; ++i) if (Compare(Y, R[i]) == 1) Y = R[i];
Answer(Y, X);
}
D2T2 - Making Friends is Fun
首先对于一个点,对于与它出边相连的所有边,这几个点最后一定会成为一个完全图。
然后你考虑一个出去的点再出去的点,发现这些点也会和原来的一圈点构成一个完全图。
然后归纳的想,那么对于每一个出度大于 \(2\) 的点,周围这一圈点以及这一圈点能够达到的点都能一起构成一个完全图。
那么最后只有两类边,一类是完全图的边,一类是中间的这个点和周围一圈的点链接的边。
对于完全图的情况,用并查集加上 dfs 维护。
时间复杂度 \(\mathcal O (n)\) 。
struct dsu {
int f[N], g[N];
inline void init(int R) {forn (i, 1, R) f[i] = i, g[i] = 1; }
int fnd(int u) {return f[u] == u ? u : f[u] = fnd(f[u]); }
void mrg(int u, int v) {
u = fnd(u), v = fnd(v);
if(u == v) return ;
g[u] += g[v], f[v] = u;
}
} O;
int n, m; vector<int> G[N];
bool vis[N];
inline void dfs(int u, int lst) {
vis[u] = 1;
for (const int& v : G[u]) if (v != lst) {
O.mrg(u, v);
if (!vis[v]) dfs (v, u);
}
}
inline i64 C2(i64 k) {return k * (k - 1);}
inline void solve() {
Rdn(n, m), O.init(n);
forn (i, 1, m) {
int u, v;
Rdn(u, v);
G[u].push_back(v);
}
i64 res = 0;
forn (u, 1, n) {
int Pre = 0;
for (const int& v : G[u]) {
if (Pre) O.mrg(v, Pre);
Pre = v;
}
}
forn (u, 1, n) if (!vis[u] && O.g[O.fnd(u)] > 1) dfs (u, u);
forn (u, 1, n) if (O.fnd(u) == u && O.g[O.fnd(u)] > 1) res += C2(O.g[O.fnd(u)]);
else if(O.fnd(u) == u) res += G[u].size();
Wtn(res, '\n');
}
D2T3 - Stamp Rally
发现对于原问题在一个车站上有 \(4\) 种决策。
- \(U_i + V_i\)
- \(D_i + E_i\)
- \(U_i + E_i\)
- \(D_i + V_i\)
第一种决策,任意时刻都能使用。
第二种决策,只有当前行可以在下行通道上的时候才能用。
如果存在 \(k\) 个第三种决策,那么在前面的行中必然出现 \(k\) 个第四种决策。
所以如果按照从 \(1\) 到 \(n\) 的顺序,每层计算贡献的话,整个过程可以看成一个括号匹配的过程。
其中第四种决策作为左括号,第三种决策作为右括号,发现剩余未匹配的左括号数量相同时,多出来的 \(T\) 的个数是相同的,所以满足子结构。
所以设 \(dp(i, j)\) 表示已经计算了前 \(i\) 行的贡献,有 \(j\) 个做括号没有匹配的因为打邮戳多出的贡献的最优解。
转移分五类。
一类是不改变括号个数,从上行转移,方程:
注意 \(E_i + D_i\) 必须在 \(j > 0\) 的时候才能转移。
一类是增加左括号个数,从上行转移,方程:
一类是匹配一个右括号,从上行转移,方程:
然后,由于一行可以匹配多个右括号,增加多个左括号,所以同行的转移就等价于对于减少或增加一个括号作为一个物品的完全背包。
时间复杂度 \(\mathcal O (n ^ 2)\) .
int n; i64 T, U[N], V[N], E[N], D[N], dp[N][N];
inline void solve() {
Rdn(n, T);
forn (i, 1, n) Rdn(U[i], V[i], D[i], E[i]);
memset(dp, 0x7f, sizeof dp);
dp[0][0] = 0;
forn (i, 1, n) {
forn (j, 0, n) {
dp[i][j] = min (dp[i][j], dp[i - 1][j] + U[i] + V[i] + T * j * 2ll);
if (j) dp[i][j] = min (dp[i][j], dp[i - 1][j] + D[i] + E[i] + T * j * 2ll);
if (j) dp[i][j] = min (dp[i][j], dp[i - 1][j - 1] + V[i] + D[i] + T * (j - 1) * 2ll);
if (j != n) dp[i][j] = min (dp[i][j], dp[i - 1][j + 1] + U[i] + E[i] + T * (j + 1) * 2ll);
}
form (j, n - 1, 0) dp[i][j] = min (dp[i][j], dp[i][j + 1] + U[i] + E[i]);
forn (j, 1, n) dp[i][j] = min (dp[i][j], dp[i][j - 1] + D[i] + V[i]);
}
Wtn(dp[n][0] + T * (n + 1), '\n');
}
D3T1 - JOIOJI
发现合法的区间 \([l, r]\) 一定满足在 \(l - 1\) 和 \(r\) 位置上的前缀 JOI 个数相互之间的差相等,所以可以用一个 std::map 存下每一个二元组 \((pre_J - pre_O, pre_O - pre_I)\) 最左边出现的位置。
如果之后再出现了这个位置,那么就更新答案。
int n, prea, preb, prec; char s[N];
struct node {
int x, y;
node () {}
node (int _x, int _y) : x(_x), y(_y) {}
inline bool friend operator < (const node& A, const node& B) {
return A.x == B.x ? A.y < B.y : A.x < B.x;
}
} ;
map<node, int> S;
inline void solve() {
Rdn(n); Rdn(s + 1);
int res = 0; S[node(0, 0)] = 0;
forn (i, 1, n) {
if (s[i] == 'J') prea ++ ;
if (s[i] == 'O') preb ++ ;
if (s[i] == 'I') prec ++ ;
if (S.count(node(prea - preb, preb - prec))) res = max(res, i - S[node(prea - preb, preb - prec)]);
else S[node(prea - preb, preb - prec)] = i;
}
Wtn(res, '\n');
}
D3T2 - Scarecrows
先排序。
点对问题考虑分治,考虑右半边点对于左半边点的贡献。
首先,由于左半边的点对于左半边的点有限制,所以要确定每一个左半边点可以接受的右半边点的范围:
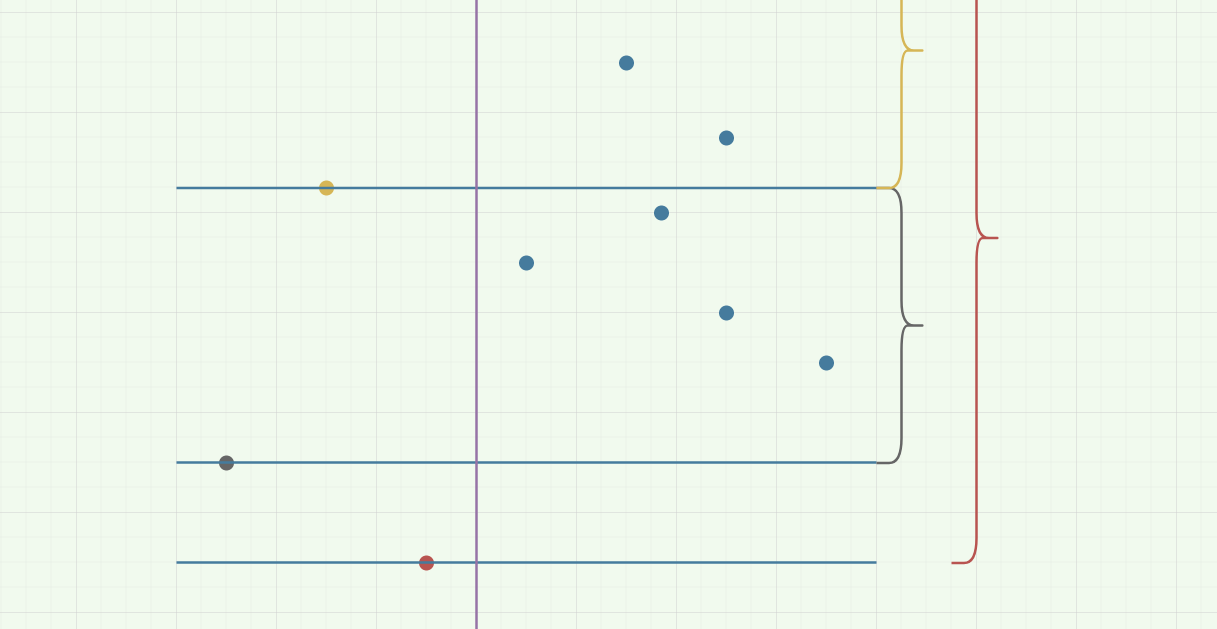
由图中可以发现,范围就是这个点的大小到这个点右边比它大的最小的点。
这一过程可以从右往左扫一遍左半边的点,用 std::set 维护。
然后考虑右边每个点对于左边能够产生贡献的范围,画出来就是下图:
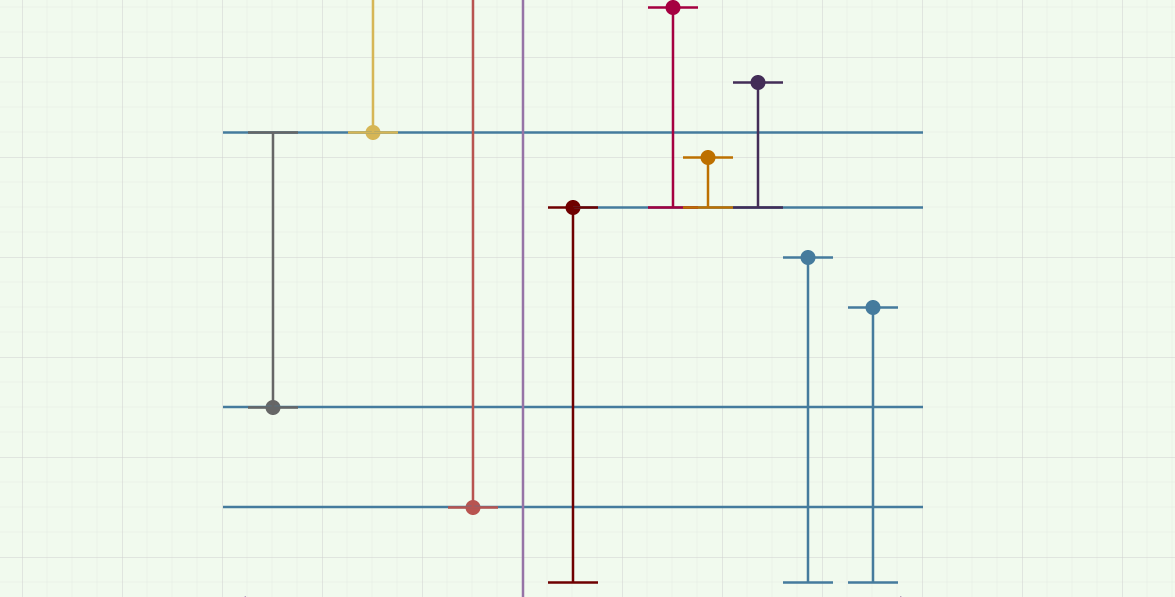
左端点就是左边比它小的最大的点。
考虑如何求答案,先把每个预处理的区间按左端点排序,在查询一个左半边点之前,先放进所有左端点小于这个点的所有右半边点代表的线段,这一部分用树状数组维护即可。
时间复杂度就是 \(\mathcal O (n\log ^ 2n)\) ,好像这样做常数巨大。。。
struct Pts {
int x, y;
Pts() {}
Pts(int _x, int _y) : x(_x), y(_y) {}
inline void Rdn() {FASTIO:: Rdn(x, y); }
inline friend bool operator < (const Pts& A, const Pts& B) {
return A.x < B.x;
}
} P[N];
struct BIT {
int val[N], R, A;
inline void upd(int p, int k) {++p ; while (p <= R) val[p] += k , p += p & -p; }
inline int qry(int p) {++p ; A = 0; while (p) A += val[p], p -= p & -p; return A; }
inline void clr(int p) {++p; while (p <= R) val[p] = 0, p += p & -p; }
} ZT;
int n, rft[N], m, liml[N], limr[N], id[N]; i64 res; set<int> S;
inline void solve() {
Rdn(n), ZT.R = n + 3;
forn (i, 1, n) P[i].Rdn(), rft[++m] = P[i].y;
sort (rft + 1, rft + m + 1);
forn (i, 1, n) P[i].y = lower_bound(rft + 1, rft + m + 1, P[i].y) - rft;
rft[++m] = 1e9 + 7;
sort (P + 1, P + n + 1);
const auto div = [&] (auto&& div, int l, int r) {
if (l == r) return ;
int mid = l + r >> 1;
div(div, l, mid), div(div, mid + 1, r);
S.clear(); S.insert(m);
form (i, mid, l) liml[i] = P[i].y, limr[i] = *S.upper_bound(P[i].y), S.insert(P[i].y), id[i] = i;
S.clear(); S.insert(0);
forn (i, mid + 1, r) liml[i] = *(--S.lower_bound(P[i].y)), limr[i] = P[i].y, S.insert(P[i].y), id[i] = i;
sort (id + l, id + mid + 1, [&] (const int& A, const int& B) {return liml[A] < liml[B]; });
sort (id + mid + 1, id + r + 1, [&] (const int& A, const int& B) {return liml[A] < liml[B]; });
int rr = mid + 1;
forn (i, l, mid) {
while (rr <= r && liml[id[rr]] <= liml[id[i]]) ZT.upd(liml[id[rr]], 1), ZT.upd(limr[id[rr]] + 1, -1), ++rr ;
res += ZT.qry(liml[id[i]]) - ZT.qry(limr[id[i]] + 1);
}
forn (i, mid + 1, r) ZT.clr(liml[i]), ZT.clr(limr[i] + 1);
} ;
div(div, 1, n);
Wtn(res, '\n');
}
D3T3 - Voltage
很巧妙的一道题,没想出如何处理 dfs 树外的信息。
首先将题意转化一下,就是求出有多少条边满足删掉这条边后为二分图且这条边的两个端点可以画为相同颜色。
那么这条边一定在(所有奇环的交集)和(所有偶环的并集的补集)的交集上。
然后你想出来在 dfs 树上找出奇环和偶环,用树上差分标记出所有树边属于的奇环和偶环数量。
然后只要奇环数量为总奇环数,偶环数量为零则答案加一。
但是这没有考虑到 dfs 树外面的信息。
比如说这个样例一,如果运气不好的话,这颗 dfs 树只会找到环 1-2-4 和 1-2-4-3,忽略了一个奇环 1-3-4 。
首先观察一下这种树外环出现的条件,首先这样的环一定存在于两个环存在一条公共边的时候,因为 dfs 树上一条返祖边默认只对应一个环。
我们把一条返祖边对应的环和在树外的环用一个吃与被吃的关系描述。
- 那么如果吃的环是奇环,被吃的环也是奇环,那么必然在外部存在一个偶环,将不是公共边的全部标记,只有内部的边合法,所以对答案没有影响。
- 如果吃的环是偶环,被吃的也是偶环,这种就很显然对答案无影响。
- 如果吃的环是奇环,被吃的是偶环,那么两个环合在一起必定有一个奇环存在,而外部的点肯定都不合法,所以成立。
- 如果吃的环是偶环,被吃的是奇环,和上种情况相同。
所以树外部的环对答案没有影响,直接按照上方的样子处理即可。
struct node {
int id, v;
node() {}
node(int _d, int _v) : id(_d), v(_v) {}
} ;
int n, m; vector<node> T[N];
int dep[N], b[N], tag[N], tbg[N], f[N], lst[N], cyc, stk[N], top; bool vis[N], vv[N];
void Fdfs(int u) {
vis[u] = 1, b[u] = b[f[u]] ^ 1, vv[u] = 1;
for (const node& v : T[u]) if(v.id != lst[u]) {
if (!vis[v.v]) f[v.v] = u, lst[v.v] = v.id, Fdfs(v.v);
else if(vv[v.v]) {
if(b[u] == b[v.v]) tag[u] ++ , tag[v.v] -- , cyc ++ ;
else tbg[u] ++ , tbg[v.v] -- ;
}
}
vv[u] = 0;
return ;
}
void Sdfs(int u) {
vv[u] = 1;
for (const node& k : T[u]) if(f[k.v] == u && !vv[k.v]) {
Sdfs(k.v); tag[u] += tag[k.v], tbg[u] += tbg[k.v];
}
return ;
}
inline void solve() {
Rdn(n, m);
forn (i, 1, m) {
int u, v; Rdn(u, v);
T[u].push_back(node(i, v));
T[v].push_back(node(i, u));
}
forn (i, 1, n) if(!vis[i]) Fdfs(i);
forn (i, 1, n) if(!vv[i]) Sdfs(i);
int res = (cyc == 1);
forn (i, 1, n) if (f[i] && tag[i] == cyc && tbg[i] == 0) res ++ ;
Wtn(res, '\n');
}
D4T1 - Constellation 2
struct Vec {
int x, y, c;
Vec() {}
Vec(int _x, int _y, int _c) : x(_x), y(_y), c(_c) {}
} O, K[N];
inline i64 Crs(const Vec& A, const Vec& B) {
return 1ll * A.x * B.y - 1ll * A.y * B.x;
}
inline Vec Tra(const Vec& P) {return (P.y >= 0) ? P : Vec(-P.x, -P.y, P.c); }
inline i64 Plo(const Vec& A, const Vec& B, const Vec& C) {
return Crs(Vec(A.x - C.x, A.y - C.y, 0), Vec(B.x - C.x, B.y - C.y, 0)) ;
}
int n, x[N], y[N], c[N]; i64 numa[3], numb[3], ans; bool up[N];
inline void solve() {
Rdn(n);
forn (i, 1, n) Rdn(x[i], y[i], c[i]);
forn (i, 1, n) {
memset(numa, 0, sizeof numa);
memset(numb, 0, sizeof numb);
forn (j, 1, i - 1) K[j] = Vec(x[j] - x[i], y[j] - y[i], c[j]);
forn (j, i + 1, n) K[j - 1] = Vec(x[j] - x[i], y[j] - y[i], c[j]);
sort (K + 1, K + n, [&] (const Vec& A, const Vec& B) {
return Crs(Tra(A), Tra(B)) < 0;
}) ;
forn (j, 1, n - 1) {
if (K[j].y < 0) up[j] = 0, numb[K[j].c] ++ ;
else up[j] = 1, numa[K[j].c] ++ ;
}
forn (j, 1, n - 1) {
if (up[j]) numa[K[j].c] -- ;
else numb[K[j].c] -- ; up[j] ^= 1;
i64 res = 1;
rep (k, 0, 3) if (k != K[j].c) res *= numa[k];
rep (k, 0, 3) if (k != c[i]) res *= numb[k];
ans += res;
res = 1;
rep (k, 0, 3) if (k != c[i]) res *= numa[k];
rep (k, 0, 3) if (k != K[j].c) res *= numb[k];
ans += res;
if (up[j]) numa[K[j].c] ++ ;
else numb[K[j].c] ++ ;
}
}
Wtn(ans >> 2, '\n');
}
D4T3 - Straps
首先发现只要钩子的数量大于等于挂饰的数量,那么一定合法。
所以设 \(f(i, j)\) 表示考虑了 \(i\) 个挂饰,还有 \(j\) 个挂饰没有用的最优解。
但是为了保证最优的情况,所以先要把所有挂饰按照 \(a\) 从大到小排序。
但是这个 DP 是 \(\mathcal O (n ^ 3)\) 的。
很容易发现,后面的 \(j\) 的状态数 \(n ^ 2\) 是假的,因为如果挂钩数量大于 \(n\),那么不管怎么样都是合法的。
这样状态数量就被控制到 \(\mathcal O (n ^ 2)\) 了。
int n, a[N], id[N]; i64 b[N], dp[N][N];
inline void solve() {
Rdn(n);
forn (i, 1, n) Rdn(a[i], b[i]), id[i] = i;
forn (i, 0, n) forn (j, 0, n + 1) dp[i][j] = -INF;
sort (id + 1, id + n + 1, [&] (const int& A, const int& B) {return a[A] > a[B];});
dp[0][1] = 0;
rep (i, 0, n) forn (j, 0, n + 1) {
dp[i + 1][j] = max(dp[i + 1][j], dp[i][j]);
if(j + a[id[i + 1]] - 1 >= 0) dp[i + 1][min(n + 1, j + a[id[i + 1]] - 1)] = max(dp[i + 1][min(n + 1, j + a[id[i + 1]] - 1)], dp[i][j] + b[id[i + 1]]);
}
i64 res = 0;
forn (i, 0, n + 1) res = max(res, dp[n][i]);
Wtn(res, '\n');
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号