JOI 2013 Final
JOI 2013 Final
T1 - Denshoku
把所有黑白交错的段记作一个独立的段,那么不难发现,对于左右不为空的段,最优情况就是把自己反转,然后对于枚举每个段反转一次的长度后就做完了。
时间复杂度 \(\mathcal O (n)\) 。
struct seg {
int l, r;
seg() {}
seg(int _l, int _r) : l(_l), r(_r) {}
} s[N];
int n, m, a[N], res;
inline void solve() {
Rdn(n);
forn(i,1,n) Rdn(a[i]);
forn(l,1,n) {
int r = l;
while (r < n && a[r + 1] == (a[r] ^ 1)) ++r;
s[++m] = seg(l, r), res = max(res, r - l + 1), l = r;
}
rep(i,2,m) res = max(res, s[i + 1].r - s[i - 1].l + 1);
if(m <= 2) res = n;
printf("%d\n", res);
}
T2 - IOI ressha de ikou
直接 DP 即可,时间复杂度 \(\mathcal O (n\times m)\) 。
int n, m, dp[N][N][2]; char S[N], T[N];
inline void solve() {
Rdn(n, m), Rdn(S + 1), Rdn(T + 1);
forn(i,1,n) S[i] = (S[i] == 'I');
forn(i,1,m) T[i] = (T[i] == 'I');
forn(i,0,n) forn(j,0,m) {
if (i && S[i]) dp[i][j][1] = dp[i - 1][j][0] + 1;
if (j && T[j]) dp[i][j][1] = max(dp[i][j][1], dp[i][j - 1][0] + 1);
if (i && !S[i] && dp[i - 1][j][1]) dp[i][j][0] = max(dp[i][j][0], dp[i - 1][j][1] + 1);
if (j && !T[j] && dp[i][j - 1][1]) dp[i][j][0] = max(dp[i][j][0], dp[i][j - 1][1] + 1);
}
int res = 0;
forn(i,1,n) forn(j,1,m) res = max(res, dp[i][j][1]);
printf("%d\n", res);
}
T3 - Gendai-tekina yashiki
发现只有起终点和可以开关的点对操作有影响,只留下这些即可。
把原图变成两个图,一个图描述东西方向,另一个图描述南北方向的情况。
只保留 \(K\) 和起终点,对于开关点,链接两图之间的边,其他边按照题意链接即可。
struct node {
int v; i64 w;
node() {}
node(int _v, i64 _w) : v(_v), w(_w) {}
inline friend bool operator < (const node& A, const node& B) {
return A.w > B.w;
}
} ;
struct pts {
int x, y, d;
pts() {}
pts(int _x, int _y, int _d) : x(_x), y(_y), d(_d) {}
} ton[N << 1];
vector<node> G[N << 1];
int n, m, k, cnt; vector<int> H[N], V[N]; bool fl1, fl2;
inline bool cmp1(int A, int B) {return ton[A].y < ton[B].y;}
inline bool cmp2(int A, int B) {return ton[A].x < ton[B].x;}
int st, ed, edd; i64 d[N << 1];
priority_queue<node> Q;
inline void solve() {
Rdn(n, m, k);
forn(i,1,k) {
++cnt;
Rdn(ton[cnt].x, ton[cnt].y);
ton[cnt + 1] = ton[cnt]; ++cnt;
ton[cnt].d = 1, G[cnt].push_back(node(cnt - 1, 1ll)), G[cnt - 1].push_back(node(cnt, 1ll));
if (ton[cnt].x == 1 && ton[cnt].y == 1) st = cnt - 1, fl1 = 1;
if (ton[cnt].x == n && ton[cnt].y == m) ed = cnt, edd = cnt - 1, fl2 = 1;
}
if (!fl1) ton[++cnt] = pts(1, 1, 0), st = cnt;
if (!fl2) ton[++cnt] = pts(n, m, 0), ed = cnt, ton[++cnt] = pts(n, m, 1), edd = cnt;
// forn(i,1,cnt) Wtn("(", ton[i].x, ", ", ton[i].y, ", ", ton[i].d, ')', " \n"[i == cnt]);
// Wtn(ed, ' ', edd, '\n');
forn(i,1,cnt) if(ton[i].d == 0) V[ton[i].x].push_back(i);
else H[ton[i].y].push_back(i);
forn(i,1,n) {
sort(V[i].begin(), V[i].end(), cmp1);
rep(j,1,V[i].size()) G[V[i][j]].push_back(node(V[i][j - 1], ton[V[i][j]].y - ton[V[i][j - 1]].y)),
G[V[i][j - 1]].push_back(node(V[i][j], ton[V[i][j]].y - ton[V[i][j - 1]].y));
}
forn(i,1,m) {
sort(H[i].begin(), H[i].end(), cmp2);
rep(j,1,H[i].size()) G[H[i][j]].push_back(node(H[i][j - 1], ton[H[i][j]].x - ton[H[i][j - 1]].x)),
G[H[i][j - 1]].push_back(node(H[i][j], ton[H[i][j]].x - ton[H[i][j - 1]].x));
}
// forn(i,1,cnt) for (const node& K : G[i]) Wtn("(", i, ", ", K.v, ")", " "); Wtn('\n');
forn(i,1,cnt) d[i] = INF;
Q.push(node(st, 0));
while(!Q.empty()) {
int u = Q.top().v; i64 w = Q.top().w; Q.pop();
if(d[u] != INF) continue ;
d[u] = w;
for (const node& K : G[u]) {
int v = K.v; w = K.w;
if(d[v] == INF) Q.push(node(v, d[u] + w));
}
}
// forn(i,1,cnt) Wtn(d[i], " \n"[i == cnt]);
i64 ans = min(d[ed], d[edd]);
Wtn(ans == INF ? -1 : ans, '\n');
}
T4 - JOIOI no tō
首先发现,IOI 和 JOI 都有 OI ,所以把前面这个字符和后面的 OI 分开考虑。
可以想到,贪心的取出最后面的 OI ,可以用一个队列维护 I 的位置,然后匹配 O 。
对于前面的两个字符,从后往前对于每个 OI 中的 O 做类似于括号匹配的东西即可。
答案有明显的单调性,二分答案后时间复杂度为 \(\mathcal O (n\log n)\) 。
int n; char S[N]; int stk[N], top, dn, vis[N];
inline bool check(int k) {
// Wtn(k, ":: \n");
int num = 0, lim = -1; top = 0, dn = 1;
memset(vis, 0, sizeof vis);
form(i,n,1) {
if(S[i] == 'I') stk[++top] = i;
else if(S[i] == 'O' && dn <= top) num ++ , vis[i] = 1, vis[stk[dn]] = 2, ++ dn ;
// Wtn(i, ' ', num, 'P');
if(num == k) {lim = i - 1; break ;}
} // Wtn('\n');
if(lim == -1) return 0;
// Wtn(k, ' ', lim, '\n');
top = 0;
// forn(i,1,n) Wtn(vis[i], " \n"[i == n]);
form(r,n,1) {
if(vis[r] == 1) stk[++top] = r;
else if(vis[r] == 0 && (S[r] == 'I' || S[r] == 'J') && top) top -- ;
// forn(i,1,top) Wtn(stk[i], " \n"[i == top]);
}
return top == 0;
}
inline void solve() {
Rdn(n), Rdn(S + 1);
int l = 1, r = n / 3, res = 0;
while (l <= r) {
int mid = l + r >> 1;
if(check(mid)) l = mid + 1, res = mid;
else r = mid - 1;
}
Wtn(res, '\n');
}
T5 - Bubble Sort
刚了一晚上没刚出来,发现少发现了一个特别重要的性质,怎么这么阴间啊。。。
将每个元素看做点 \((i, a_i)\),那么每个点形成的逆序对个数就是每个点左上和右下的点个数之和,那么交换的结果就像下图:
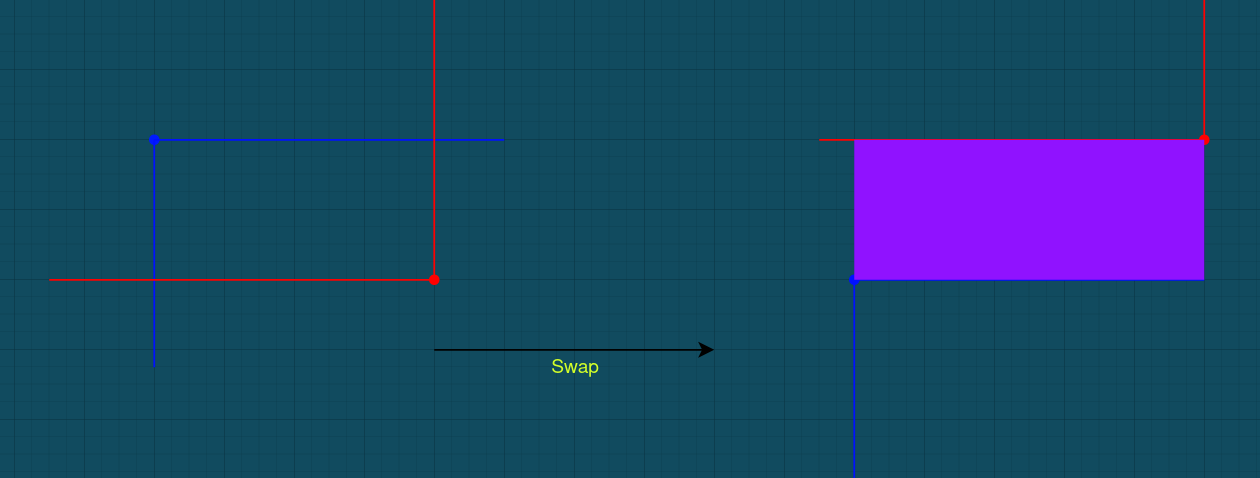
发现少掉的逆序对个数等于紫色区域内部点数的两倍加上紫色区域边缘点数的一倍。
然后你试图暴力扫描线搞这个东西,结果失败了。
然后你发现一件非常神仙的事情,就是如果被交换的左端点或者右端点是最优的,那么左端点 \(l\) 满足 \(\max_{1\le k\le l} a_k = a_l\) ,右端点满足 \(\min_{r\le k\le n} a_k = a_r\) 。
因为不取这样的点,那么这个左/右端点的左/右端必定有一个比它更优秀。
这样的一个好处就是左右端点都具备了单调性。
有了这个性质,事情变得明了起来。
你试图枚举右端点,同时维护每个左端点的答案,并快速求出最值。
但是事情没有这么简单,所以考虑每个点对于每个左右端点的贡献。
然后对于左端点作为 \(x\) 轴,右端点作为 \(y\) 轴,做扫描线。
对于每个点,二分找出在左、右端点数组中的合法位置区间,对于在紫色区域内,紫色边缘上的情况分别讨论,先离线得出每一条扫描线,然后排序扫一遍即可。
时间复杂度 \(\mathcal O (n\log n)\) 。
struct BIT {
int val[N], R, A;
inline void upd(int p, int k) {while (p <= R) val[p] += k, p += p & -p; }
inline int qry(int p) {A = 0; while (p) A += val[p], p -= p & -p; return A; }
} T;
int n, a[N], pre[N], suf[N], rft[N], m; i64 res, ans;
inline void calc() {
T.R = m;
form(i,n,1) res += T.qry(a[i] - 1), T.upd(a[i], 1);
}
struct SGT {
i64 val[N << 2], tag[N << 2];
inline void up(int p) {val[p] = max(val[p << 1], val[p << 1 | 1]); }
inline void opt(int p, int k) {val[p] += k, tag[p] += k; }
inline void down(int p) {opt(p << 1, tag[p]), opt(p << 1 | 1, tag[p]), tag[p] = 0; }
void upd(int p, int l, int r, int nl, int nr, int k) {
if(nl == l && r == nr) return opt(p, k);
int mid = nl+nr >> 1;
(tag[p]) && (down(p), 0);
if(r <= mid) upd(p << 1, l, r, nl, mid, k);
else if(l > mid) upd(p << 1 | 1, l, r, mid + 1, nr, k);
else upd(p << 1, l, mid, nl, mid, k), upd(p << 1 | 1, mid + 1, r, mid + 1, nr, k);
up(p);
}
} ZT;
struct Line {
int l, r, x, v;
Line() {}
Line(int _l, int _r, int _x, int _v) : l(_l), r(_r), x(_x), v(_v) {}
} ton[N << 2]; int num;
int L[N], R[N], numL, numR;
inline void solve() {
Rdn(n);
forn(i,1,n) Rdn(a[i]), rft[++m] = a[i];
sort(rft + 1, rft + m + 1);
m = unique(rft + 1, rft + m + 1) - rft - 1;
forn(i,1,n) a[i] = lower_bound(rft + 1, rft + m + 1, a[i]) - rft ;
calc();
// Wtn(res, '\n');
if(res == 0) {
sort(a + 1, a + n + 1);
rep(i,1,m) if(a[i] == a[i + 1]) return Wtn("0\n");
return Wtn("1\n");
}
// forn(i,1,m) Wtn(rft[i], " \n"[i == m]);
forn(i,1,n) pre[i] = max(pre[i - 1], a[i]); suf[n + 1] = m + 1;
form(i,n,1) suf[i] = min(suf[i + 1], a[i]); a[0] = 0;
forn(i,1,n) if(a[i] == pre[i] && a[i] > a[L[numL]]) L[++numL] = i; a[0] = m + 1;
form(i,n,1) if(a[i] == suf[i] && a[i] < a[R[numR]]) R[++numR] = i;
reverse(R + 1, R + numR + 1);
// forn(i,1,numL) Wtn(L[i], " \n"[i == numL]);
// forn(i,1,numR) Wtn(R[i], " \n"[i == numR]);
forn(i,1,n) {
int Ll = lower_bound(L + 1, L + numL + 1, i, [&](const int& A, const int& B) {return a[A] < a[B]; }) - L;
int Lr = lower_bound(L + 1, L + numL + 1, i) - L - 1;
int Rl = upper_bound(R + 1, R + numR + 1, i) - R;
int Rr = upper_bound(R + 1, R + numR + 1, i, [&](const int& A, const int& B) {return a[A] < a[B]; }) - R - 1;
// Wtn(Ll, ' ', Lr, ' ', Rl, ' ', Rr, '\n');
if(L[Ll] == i || R[Rr] == i) continue ;
if(a[L[Ll]] == a[i] && Rr - (a[R[Rr]] == a[i]) >= Rl) {
ton[++num] = Line(Rl, Rr - (a[R[Rr]] == a[i]), Ll, 1);
ton[++num] = Line(Rl, Rr - (a[R[Rr]] == a[i]), Ll + 1, -1);
}
if(a[L[Ll]] == a[i]) ++Ll;
if(a[R[Rr]] == a[i] && Ll <= Lr) {
ton[++num] = Line(Rr, Rr, Ll, 1);
ton[++num] = Line(Rr, Rr, Lr + 1, -1);
--Rr;
}
if(Ll <= Lr && Rl <= Rr) {
ton[++num] = Line(Rl, Rr, Ll, 2);
ton[++num] = Line(Rl, Rr, Lr + 1, -2);
}
}
sort(ton + 1, ton + num + 1, [&](const Line& A, const Line& B) {return A.x < B.x; }) ;
// forn(i,1,num) Wtn("(", ton[i].x, ", [", ton[i].l, ", ", ton[i].r, "]):: ", ton[i].v, "\n"); flush();
forn(l,1,num) {
int r = l;
while (r < num && ton[l].x == ton[r + 1].x) ++r;
forn (s, l, r) ZT.upd(1, ton[s].l, ton[s].r, 1, m, ton[s].v);
// Wtn(l, ' ', r, '\n');
ans = max(ans, ZT.val[1]); l = r;
}
Wtn (res - ans - 1, '\n');
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号