题解：Mirror Mirror
Problem Statement
设一个字符串 \(U\) ，则 \(\rm U[l : r]\) 表示 \(U\) 中第 \(l\) 个到第 \(r\) 个字符形成的子串，\(\rm rev (U)\) 表示将字符串 \(U\) 反转后的结果。
给你一个长度为 \(N\) 的字符串 \(S\) 和一个长度为 \(M\) 的字符串 \(T\) 。
现在可以对字符串 \(S\) 进行如下两个操作，每种操作可以使用任意的次数，整串操作可以在任意顺序下进行：
- 选择 \(1\le i \le |S|\) ，将 \(S\) 换成 \(\rm S[1 : i] + rev(S[1 : i])\) 。
- 选择 \(1\le i \le |S|\) ，将 \(S\) 换成 \(\rm rev(S[i : |S|]) + S[i : |S|]\) 。
判断是否可以在如上条件下将 \(S\) 变成 \(T\) 。
若不可以，输出 \(-1\) ，若可以，输出最小的操作次数。
Constrainst
- \(1\le N, M \le 2 \times 10 ^ 7\)
- \(S\) 和 \(T\) 由小写字母组成。
- \(S \neq T\)
- \(N\) 和 \(M\) 是整数。
solution
首先判断一定无解的情况，trivial 的情况如下：
- \(S \neq T\) ，\(T\) 的长度为奇数。
- \(S \neq T\) ，\(T\) 不是回文串。
发现第一次操作比较特殊，考虑其他建立于回文串的操作的性质。
首先，由于是回文串，第一种操作选择 \(i\) ，那么必然有一个第二种操作与其等价，所以只需考虑第一种操作即可。
由于生成的串原来也是回文串，所以设串的长度为 \(2L\) ，那么最优情况下，会选择大于 \(L\) 的 \(i\) 进行操作。
因为若选择小于 \(L\) 的 \(i\) ，这样得到的结果在上一步中也可以一步完成，是一种浪费。
那么现在有一个很有用的性质，那就是操作时候的串会不断增长。
由于是回文串，我们只考虑所有回文串前一半的东西，那么每次的操作就如下图：
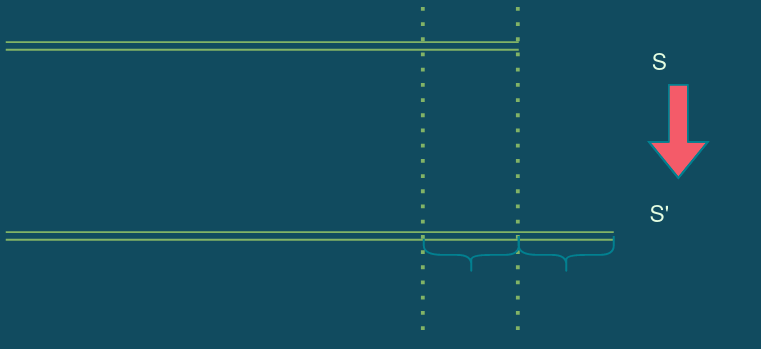
所以每次操作相当于把一个后缀接到整个字符串后面。
这样我们就可以画出 \(T\) 的大概样子了：
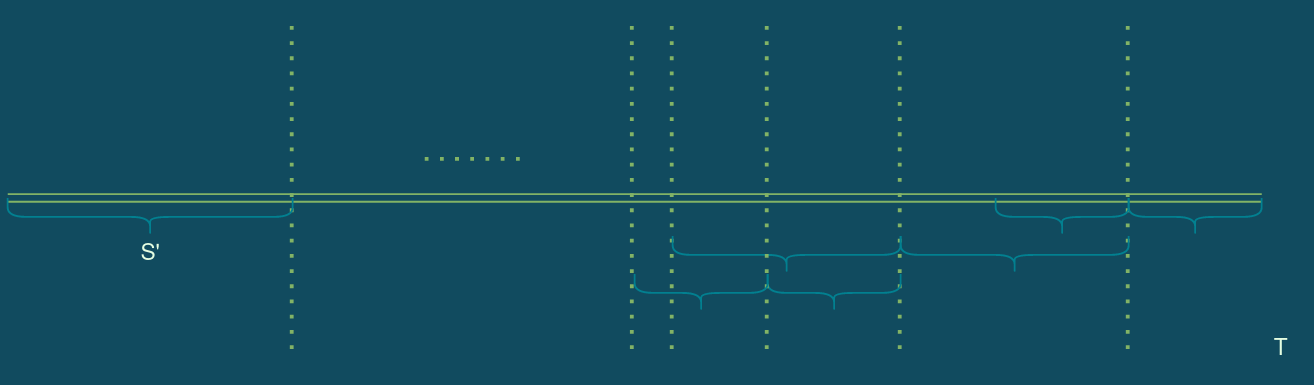
\(S'\) 表示经过第一次操作形成的一个字符串，那么在之后的所有操作中，最优情况下 \(S\) 必须一直是 \(T\) 的一个前缀。
所以设 \(dp_i\) 表示形成字符串 \(T\) 前缀长度为 \(i\) 的最少操作。
由于两个括号中的东西一定是回文，所以可以预处理出中心为 \(i - 1\) 和 \(i\) 的偶回文串的最长长度 \(d_i\) ，这个可以用 Manacher 算法求出，那么转移也很明显了。
初始状态就是第一步能形成的前缀，转移就是:
直接线段树维护即可，时间复杂度 \(\mathcal O(N + M\log M)\) 。
观察一下 \(dp\) 数组的性质，发现事情不简单，由于若 \(i + 1\) 位置能被转移到，那么对于 \(i\) 位置，要么是 \(i\) 转移到 \(i + 1\) ，要么 \(i\) 比 \(i + 1\) 受到相同或更左方的转移，所以有 \(dp_i \le dp_j \ (i\le j)\) 。
那么，对于每个 \(i\) ，只要记录最左边的转移点即可，那么维护一个数组 \(g_i\) ，先令 \(g_{i + d_i - 1} = i - 1\) ，取最小的 \(i - 1\) ，然后对这个 \(g\) 做一个后缀 \(\min\) 即可。
最后转移就变成了 \(dp_i = \min\{dp_i, dp_{g_i} + 1\}\) 。
时间复杂度 \(\mathcal O (N + M)\) 。
