AtCoder Grand Contest 002
C - Knot Puzzle
逆向思维，从后往前考虑，发现最终的局面必定是两个加起来大于 \(L\) 的相邻元素，只要寻找并判断这个位置是否存在即可。
int n, a[N], L;
inline void solve() {
Rdn(n, L);
forn(i,1,n) Rdn(a[i]);
int pos = -1;
rep(i,1,n) if(a[i] + a[i + 1] >= L) {pos = i; break ;}
if(pos == -1) return Wtn("Impossible\n");
Wtn("Possible\n");
rep(i,1,pos) Wtn(i, '\n');
form(i,n - 1,pos + 1) Wtn(i, '\n');
Wtn(pos, '\n');
}
D - Stamp Rally
二分＋克鲁斯卡尔重构树。
struct dsu {
int fa[N];
inline void init(int R) {forn(i,1,R) fa[i] = i;}
int fnd(int u) {return fa[u] == u ? u : fa[u] = fnd(fa[u]);}
inline void mrg(int u, int v) {
u = fnd(u), v = fnd(v);
if(u == v) return ;
fa[v] = u;
}
} O;
int n, m, cc, u[N], v[N], Q, L[N], R[N], fa[19][N], siz[N], val[N];
void dfs(int u) {
siz[u] = (u <= n);
if(L[u]) dfs(L[u]), siz[u] += siz[L[u]];
if(R[u]) dfs(R[u]), siz[u] += siz[R[u]];
}
inline int check(int x, int y, int mid) {
form(i,18,0) if(val[fa[i][x]] <= mid) x = fa[i][x];
form(i,18,0) if(val[fa[i][y]] <= mid) y = fa[i][y];
if(x == y) return siz[x];
return siz[x] + siz[y];
}
inline void solve() {
Rdn(n, m), O.init(n << 1), cc = n, val[0] = m + 114514;
forn(i,1,m) {
Rdn(u[i], v[i]);
if(O.fnd(u[i]) != O.fnd(v[i])) {
L[++cc] = O.fnd(u[i]), R[cc] = O.fnd(v[i]), val[cc] = i;
fa[0][O.fnd(u[i])] = cc, fa[0][O.fnd(v[i])] = cc;
O.mrg(cc, u[i]), O.mrg(cc, v[i]);
}
}
forn(i,1,18) forn(j,1,cc) fa[i][j] = fa[i - 1][fa[i - 1][j]];
dfs(cc);
// forn(i,1,cc) Wtn(siz[i], " \n"[i == cc]);
// forn(i,1,cc) Wtn(L[i], " \n"[i == cc]);
// forn(i,1,cc) Wtn(R[i], " \n"[i == cc]);
Rdn(Q);
while(Q--) {
int x, y, z;
Rdn(x, y, z);
int l = 1, r = m, mid, res = n;
while(l <= r) {
mid = l+r >> 1;
if(check(x, y, mid) >= z) res = mid, r = mid - 1;
else l = mid + 1;
}
Wtn(res, '\n');
}
}
E - Candy Piles
由于删除的永远是最大的，所以对于原序列排序，那么每次直接删除的列都是最右边的。
由于是个有向图游戏，这个时候你想到要确定一个状态能表示每一种情况，并且能够算出它是必败还是必胜的。
对于每一个 \(j \le a_i\) ，设 \((i, j)\) 表示一颗糖，那么操作一就是去掉后面一整列，操作二就是将最下面一层给切掉。
不妨设状态为点 \((i, j)\) ，以这个点作为原点，状态设为这个新建出来的坐标轴的第二象限上剩余的点。
那么原来坐标轴 \(x = s\) 上的点的个数就是第 \(s\) 堆糖剩余的数量。
那么 \((i, j) \rightarrow (i + 1, j)\) 就是操作二，\((i, j) \rightarrow (i - 1, j)\) 就是操作一。
初始图的边境均为必胜态。
于是你画了画图，发现必胜态和必败态都是连续的以对角线形式存在的，尝试简单证一下。
设 w 表示必胜态，l 表示必败态，那么,
当 \((i, j)\) 为 w 时，有以下情况：
w w
w l
l w
w l
w w
w w
当 \((i, j)\) 为 l 时，有以下情况：
w l
l w
所以得证。
那么 \((n, 1)\) 等价于任意合法的 \((n - k, k + 1)\) 。
找到最左上的这样的节点，其左方和上方节点的胜负态取决于该坐标与左方轮廓和上方轮廓的奇偶性，然后代码就比较短了。
int n, a[N];
inline void solve() {
Rdn(n);
forn(i,1,n) Rdn(a[i]);
sort(a + 1, a + n + 1, greater<int>());
int pos = n;
forn(i,1,n) {
if(a[i] <= i || a[i + 1] <= i) {
pos = i;
break ;
}
}
int l = 0;
while(a[pos + l + 1] >= pos) ++l;
int r = a[pos] - pos;
// Wtn(pos, ' ', l, ' ', r, '\n');
Wtn(((l & 1) || (r & 1)) ? "First\n" : "Second\n");
}
F - Leftmost Ball
官解好 nb 。
如果确定每个白球对应一种颜色，那么原问题等价于求出下图的拓扑序个数：
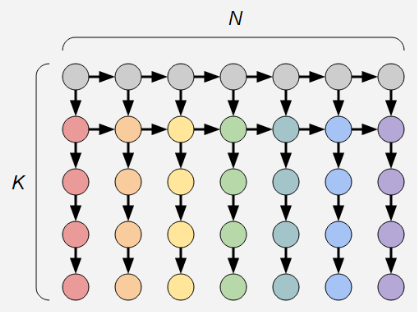
然后设 \(f(i, j)\) 表示下面子图的一个拓扑序数量：
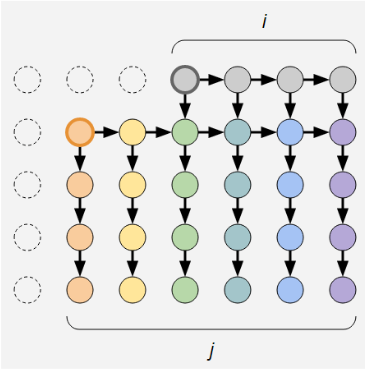
考虑转移，第一种情况是从加黑的灰点的开始，那么方案数为 \(f(i - 1, j)\) ，第二种情况是从橙点开始，那么方案数为 \({j\times (k - 1) + i - 1 \choose k - 2} \times f(i, j - 1)\) 。
直接 \(\mathcal O (N ^ 2)\) 递推即可。
int n, k; Mint f[N][N];
inline void solve() {
Rdn(n, k), table();
if(k == 1) return Wtn("1\n");
f[0][0] = Mint(1);
forn(i,1,n) f[0][i] = f[0][i - 1] * C(0 + i * (k - 1) - 1, k - 2);
forn(i,1,n) forn(j,i,n) f[i][j] = f[i - 1][j] + f[i][j - 1] * C(i + j * (k - 1) - 1, k - 2);
Wtn((f[n][n] * fac[n]).res, '\n');
}
