题解：「九省联考 2018」林克卡特树

题面

题意简述

给一棵有 \(n\) 个节点的树，将其分成 \(k+1\) 条链，求最大权值。

题解

对于 \(10\%\) 的数据，求一遍树的直径即可。

对于 \(20\%\) 的数据，考虑如何得到两条链，对情况进行分类讨论。

1. 两条链与直径均不相交。这显然不成立，因为只要有其中一条链变成直径答案就会更优。

2. 只有一条与直径相交。不成立，这条链变成直径显然更优。

3. 一条链在直径外，另一条就是直径。由上述情况易得这种情况可能是最优解。

4. 两条链都与直径相交，但是直径的两个端点并不全在链内。(黑线为直径，黄色的为两条链)
   
   从上图可以看出 \(r > r'\) ，所以该情况不成立。

5. 两条链都与直径相交，直径的两个端点全在两条链内。结合上种情况讨论，显然可能为最优解。

得出结论：当直径两个端点都在两条链中时，可能为最优解。直接贪心即可。

对于 \(45\% - 60\%\) 的数据，考虑 DP 。

设 \(f(i,j,0/1/2)\) 表示在以 \(i\) 为根的子树中，选了 \(j\) 条链，点 \(i\) 的度数为 \(\text{0/1/2}\) 时的最优解。

可以发现度数为 \(1/2\) 的状态通过简单转化后也满足度数为 \(0\) 的状态的性质，所以有：

\[f(i,j,0) \gets \max\{f(i,j,0), f(i,j-1,1), f(i,j,2)\} \]

接下来分类讨论( \(v\) 表示 \(i\) 节点的子节点， \(val(u,v)\) 表示边 \(u\rightarrow v\) 的边权)。

1. \(i\) 不连接子节点。

\[f(i,j,0) \gets \max\{f(i,j,0), f(v,k,0) + f(i,j-k,0)\} \]

2. \(i\) 与一个子节点相连。

\[f(i,j,1) \gets \max\{f(i,j,1), f(i,j-k,1)+f(v,k,0), f(i,j-k,0)+f(v,k-1,0)+val(i,v)\} \]

3. \(i\) 作为一条链的中间一点。

\[f(i,j,2) \gets \max\{f(i,j,2), f(i,j-k,2)+f(v,k,0), f(i,j-k,1)+f(i,k-1,1)+val(i,v)\} \]

对于 \(100\%\) 的数据，考虑优化 DP ，深入查找性质。

由于是取物品求最值的问题，不妨考虑单调性质，但似乎只有答案呈凸包状后有点前途。

于是设 \(g(k)\) 表示分为 \(k\) 条链的最优解，尝试证明 \(g(k+1)-g(k)\geq g(k+2)-g(k+1)\) 。

延续上面小数据的思路，试图将其拓展到更大的情况中。

引理：在 \(g(k) \rightarrow g(k+1)\) 的过程中，进行一次操作，操作为要么多取了一条链，要么将一条链分裂了。

---

引理证明：

这里 \(g(k)\) 的状态为任意一种可能的最优状态，设 \(g'(k)\) 表示一种可能的非最优解状态。

命题转化为「由 \(g(k)\) 进行一次操作后一定比由 \(g'(k)\) 进行一次操作同样优秀或者更优。」

这就转化成了上述直径变双链的相似问题，做相同的端点讨论后可以得到此命题的正确性。

---

对于先裂后取，连取两链，连裂两次，都可以用简单贪心的思路证明。

对于先取后裂的情况:

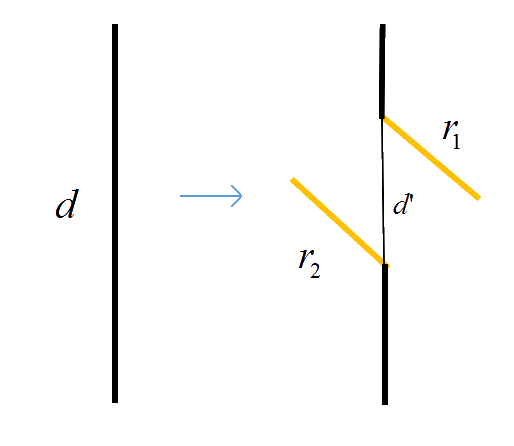
只要证明 \(d \geq r_1 + r_2 - d'\) 即可，简单移项即可完成证明:

\[d+d' \geq r_1 + r_2 \]

\[2d \geq r_1 + r_2 + d - d' \]

所以 \(g(k)\) 的图像为非严格凸包。

之后就可以放心地进行凸优化 DP 了。

时间复杂度 \(\mathcal{O}(n\log \text{A})\) 。

Code(C++): Link.