题解：Luogu P6794 [SNOI2020] 水池

题面

先观察操作，了解我们要维护什么

0. i x h

稍加思考发现将一格水面提升至 \(h\) 高度会影响到从该格向左到第一个左隔板高于 \(h\) 以及该格向右到第一个右隔板高于 \(h\) 的所有格子

所以为维护此操作，我们要查询上述的最左最右格以及修改被影响部分的水面高度

自然我们要维护区间左右隔板的最大值来支持线段树上二分查找

1. i x

看起来比较复杂，但可以想出一般规律

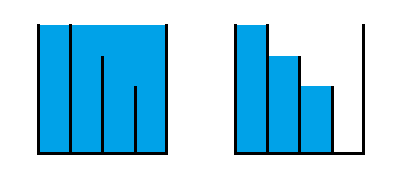
这是样例的图，观察一下会发现，相似于 opt.0 ，设原第 x 格高度 \(h'\) ，会影响到从该格向左到第一个左隔板高于 \(h'\) 以及该格向右到第一个右隔板高于 \(h'\) 的所有格子

而每个格子的最终水面高度是其在拓展方向（向左，向右）前的隔板高度的最大值

第一个查询于 opt0 相似，第二个修改只要注意递归顺序，记录最值就行

2. i x h

直接单点修改即可

3. i x

直接单点查询即可

---

用可持久化线段树维护

整理完后发现需要维护的有区间左隔板最值，区间右隔板最值，单点水量即可

标记共有 3 个，opt0 的覆盖以及 opt1 向左和向右两个标记

Code(C++):

#include<bits/stdc++.h>
#define forn(i,s,t) for(int i=(s);i<=(t);++i)
using namespace std;
const int N = 2e5+3,INF = 1e9+7;
char ch;
template<typename T>inline void redn(T &ret) {
	ret=0,ch=getchar();
	while(!isdigit(ch)) ch=getchar();
	while(isdigit(ch)) ret=(ret<<1)+(ret<<3)+ch-48,ch=getchar();
}
int n,q,a[N];
struct PreSegTree {
	int val[N<<6],L[N<<6],R[N<<6],lmx[N<<6],rmx[N<<6],tag[N<<6]; // tag: 1 cover, 2 left pour , 3 right pour
	int rt[N],sl;
	inline int Ads(int pre) {
		val[++sl] = val[pre],
		L[sl] = L[pre],R[sl] = R[pre],
		lmx[sl] = lmx[pre],rmx[sl] = rmx[pre],
		tag[sl] = tag[pre];
		return sl;
	}
	inline void push_up(int p) {
		lmx[p] = max(lmx[L[p]],lmx[R[p]]);
		rmx[p] = max(rmx[L[p]],rmx[R[p]]);
	}
	void Bld(int &p,int l,int r) {
		p = ++sl;
		if(l == r) {
			lmx[p] = a[l-1];
			rmx[p] = a[r];
			return ;
		}
		int mid = l+r >> 1;
		Bld(L[p],l,mid),Bld(R[p],mid+1,r);
		push_up(p);
	}
	void push_down(int p) {
		L[p] = Ads(L[p]),R[p] = Ads(R[p]);
		switch(tag[p]) {
			case 1: 
				val[L[p]] = val[R[p]] = val[p];
				tag[L[p]] = tag[R[p]] = 1;
				break ;
			case 2:
				val[L[p]] = max(val[p],lmx[R[p]]);
				val[R[p]] = val[p];
				tag[L[p]] = tag[R[p]] = 2;
				break ;
			case 3:
				val[L[p]] = val[p];
				val[R[p]] = max(val[p],rmx[L[p]]);
				tag[L[p]] = tag[R[p]] = 3;
		}
		tag[p] = 0;
	}
	void Lpour(int &p,int l,int r,int nl,int nr,int &now) {      // opt1 向左
		p = Ads(p);
		if(l == nl&&nr == r) {
			val[p] = now; tag[p] = 2;
			now = max(now,lmx[p]);
			return ;
		}
		tag[p]&&(push_down(p),0);
		int mid = nl+nr >> 1;
		if(r<=mid) Lpour(L[p],l,r,nl,mid,now);
		else if(l>mid) Lpour(R[p],l,r,mid+1,nr,now);
		else Lpour(R[p],mid+1,r,mid+1,nr,now),
			 Lpour(L[p],l,mid,nl,mid,now);
	}
	void Rpour(int &p,int l,int r,int nl,int nr,int &now) {       // opt1 向右
		p = Ads(p);
		if(l == nl&&nr == r) {
			val[p] = now; tag[p] = 3;
			now = max(now,rmx[p]);
			return ;
		}
		tag[p]&&(push_down(p),0);
		int mid = nl+nr >> 1;
		if(r<=mid) Rpour(L[p],l,r,nl,mid,now);
		else if(l>mid) Rpour(R[p],l,r,mid+1,nr,now);
		else Rpour(L[p],l,mid,nl,mid,now),
			 Rpour(R[p],mid+1,r,mid+1,nr,now);
	}
	int findl(int p,int l,int r,int pos,int tmp) {               // 寻找左端点
		if(lmx[p] < tmp) return -1;
		if(l == r) return l;
		int mid = l+r >> 1,res = -1;
		tag[p]&&(push_down(p),0);
		if(pos<=mid) res = findl(L[p],l,mid,pos,tmp);
		else {
			res = findl(R[p],mid+1,r,pos,tmp);
			if(res == -1) 
				res = findl(L[p],l,mid,pos,tmp);
		}
		return res;
	}
	int findr(int p,int l,int r,int pos,int tmp) {              // 寻找右端点
                if(rmx[p] < tmp) return -1;
		if(l == r) return l;
		int mid = l+r >> 1,res = -1;
		tag[p]&&(push_down(p),0);
		if(pos>mid) res = findr(R[p],mid+1,r,pos,tmp);
		else {
			res = findr(L[p],l,mid,pos,tmp);
			if(res == -1) 
				res = findr(R[p],mid+1,r,pos,tmp);
		}
		return res;
	}
	void cover(int &p,int l,int r,int nl,int nr,int k) {         // 覆盖
		p = Ads(p);
		if(l == nl && nr == r) {
			val[p] = k,tag[p] = 1;
			return ;
		}
		int mid = nl+nr >> 1;
		tag[p]&&(push_down(p),0);
		if(r<=mid) cover(L[p],l,r,nl,mid,k);
		else if(l>mid) cover(R[p],l,r,mid+1,nr,k);
		else cover(L[p],l,mid,nl,mid,k),
			 cover(R[p],mid+1,r,mid+1,nr,k);
	}
	void Chg(int &p,int l,int r,int pos,int k,int opt) {         // 单点修改
		p = Ads(p);
		if(l == r) {
			opt?rmx[p]=k:lmx[p]=k;
			return ;
		}
		tag[p]&&(push_down(p),0);
		int mid = l+r >> 1;
		if(pos<=mid) Chg(L[p],l,mid,pos,k,opt);
		else Chg(R[p],mid+1,r,pos,k,opt);
		push_up(p);
	}
	int Qry(int p,int l,int r,int pos) {                          // 单点查询
		if(l == r) return val[p];
		int mid = l+r >> 1;
		tag[p]&&(push_down(p),0);
		if(pos<=mid) return Qry(L[p],l,mid,pos);
		else return Qry(R[p],mid+1,r,pos);
	}
}T;
int main() {
	redn(n),redn(q);
	forn(i,1,n-1) redn(a[i]); a[n] = a[0] = INF;
	T.Bld(T.rt[0],1,n);
	int opt,h,x,pos,tmp,L,R;
	forn(i,1,q) {
		redn(opt),redn(x),redn(pos);
		if(!(opt&1)) redn(h);
		T.rt[i] = T.rt[x];
		switch(opt) {
			case 0:
				tmp = T.Qry(T.rt[i],1,n,pos);
				if(tmp < h) {
					L = T.findl(T.rt[i],1,n,pos,h);
					R = T.findr(T.rt[i],1,n,pos,h);
					T.cover(T.rt[i],L,R,1,n,h);
				}
				break ;
			case 1:
				tmp = T.Qry(T.rt[i],1,n,pos);
				L = T.findl(T.rt[i],1,n,pos,tmp);
				R = T.findr(T.rt[i],1,n,pos,tmp);
				tmp = 0,T.Lpour(T.rt[i],L,pos,1,n,tmp);
				tmp = 0,T.Rpour(T.rt[i],pos,R,1,n,tmp);
				break ;
			case 2:
				T.Chg(T.rt[i],1,n,pos+1,h,0);
				T.Chg(T.rt[i],1,n,pos,h,1);
				break ;
			case 3:
				printf("%d\n",T.Qry(T.rt[i],1,n,pos));
		}
	}
	return 0;
}