01背包问题

"""
有N件物品和容量是V的背包. 每件物品只能使用一次.
第i件物品的体积是Vi, 价值是Wi
求解 将哪些物品装入背包,可使这些物品的总体积不超过背包容量,总价值最大.
输出最大价值

输入格式
第一行两个整数. N V 空格隔开, 分别表示物品数量和背包容量
接下来有N行, 每行两个整数Vi , Wi, 用空格隔开, 分别表示第i件物品的体积和价值.

输出格式
输出一个整数, 表示最大值
"""

"""
输入样例:
4 5
1 2
2 4
3 4
4 5
输出样例:
8
输入样例:
4 10
8 9
3 3
4 4
3 3
输出样例:
10
"""
"""
01背包思路:
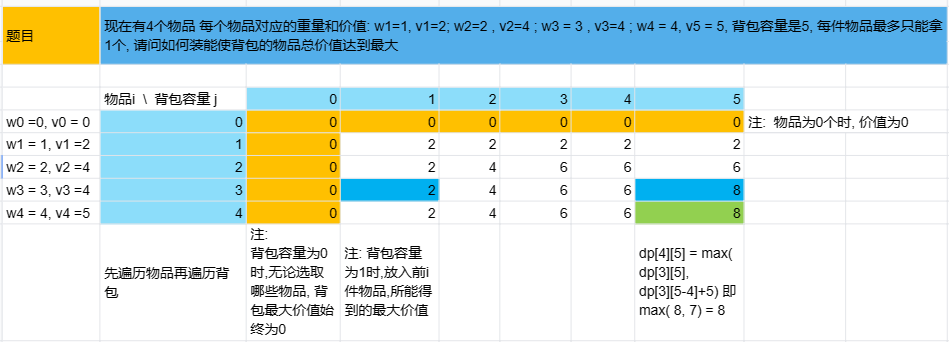
f[i][j]: 最大价值 . 从第0~第i件物品中选取物品放入容量为j的背包中, 所得到的最大总价值.
对于01背包问题选择方法的集合可以分成2种:
(1) 背包容量j 如果装不下物品i, 那么最大价值 f[i][j] = f[i-1][j]
(2) 背包容量j 如果可以装下物品i, 那么最大价值 f[i][j] = max( f[i-1][j], f[i-1][j-w[i]]+v[i] )

其中(2)可以理解为: 虽然可以装下物品i,但是一种情况: 选取了物品i,才获得最大价值; 另一种情况: 不选物品i, 就获得最大价值

w[i]: 第i个物品的重量或体积
v[i]: 第i个物品的价值

对于(2) 这种情况,我们很难计算, 因此需要思考从另一个角度解决问题. 当选择0~i个物品, 总体积不大于j的集合的最大值可以转化成:
选择0~i-1个物品, 总体积不大于j-w[i]的集合 + 最后一个物品的价值 f[i-1][j-w[i]]+ v[i]
"""

nums, v = [int(i) for i in input().split()]

weight = [0] # 初始化物品重量为0
value = [0] # 初始化物品价值为0

for i in range(nums):
l = [int(x) for x in input().split()]
weight.append(l[0])
value.append(l[1])

dp = [ [0 for j in range(v+1)] for i in range(nums+1) ]

for i in range(1,nums+1):
for j in range(v+1):
if j >= weight[i]:
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+ value[i])
else:
dp[i][j] = dp[i-1][j]

print(dp[nums][v])

 

暴力破解: